El concepto del límite de una función es fundamental para el estudio del Cálculo Diferencial e Integral, puesto que la derivada y la integral de una función están relacionadas con el concepto mencionado. Aprender sobre el límite de la función facilitará el estudio y la resolución de problemas que involucran procesos infinitos.
Problemas que dan entrada al concepto del límite de una función
En este apartado se presentan problemas que involucran procesos infinitos, cuya resolución te permitirá un primer acercamiento al concepto del límite de una función. Los problemas que vamos a revisar se remontan hasta la antigua Grecia cuando los matemáticos buscaron obtener la pendiente de la recta tangente a una función en un punto de tangencia y la velocidad instantánea de un objeto que cae libremente.
Problema 1. Pendiente de la recta tangente
El problema consiste en determinar la pendiente de la recta tangente a la gráfica de la función $f\left(x\right)=\frac{1}{2}x^2$ en el punto de tangencia $T(4,8)$, mediante la pendiente de rectas secante cuando el punto $A$ sobre la gráfica de la función se aproxima en la dirección del punto de tangencia $T$, tal como, se muestra en la figura.
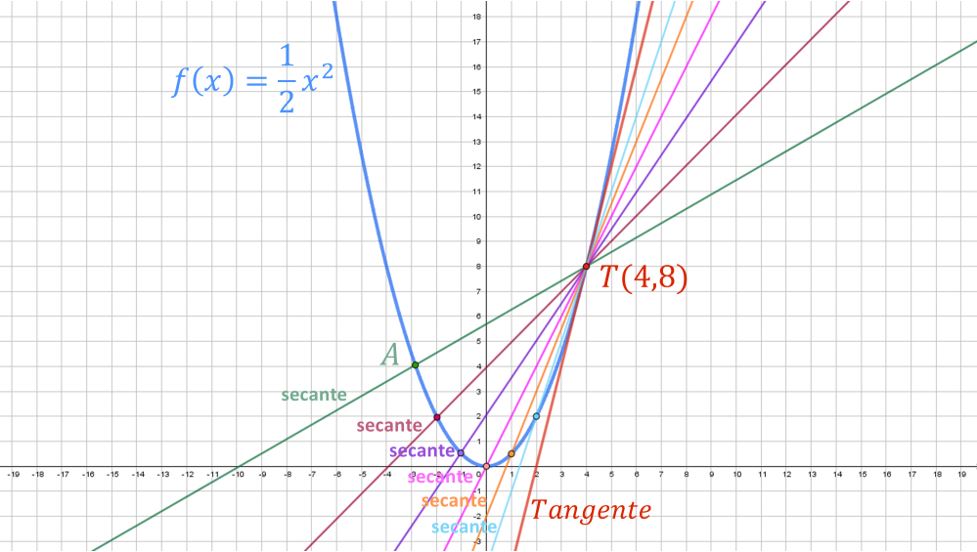
- ¿La construcción de las rectas secantes será un proceso infinito?
- ¿Cuál es el límite de las rectas secantes?
- ¿Cómo se calcula la pendiente de las rectas secantes?
- ¿Cuál será el límite de las pendientes de las rectas secantes?
Al revisar el material lograrás los aprendizajes que te permitirán contestar las preguntas.
A) Proceso de construcción de rectas secantes
En este apartado comprenderás el proceso de construcción de las rectas secantes que determina los puntos $A$ y $T$ cuando el punto $A$ se aproxima al punto de tangencia $T$. En el recorrido el punto A pasa por diferentes puntos de la gráfica de la función $f\left(x\right)=\frac{1}{2}x^2$ hacia el punto de tangencia; al unirlos con el punto de tangencia $T$ mediante una línea recta se construyen las rectas secantes. Para una mayor comprensión en la construcción de las rectas secantes revisa el siguiente video.
En el video se te presentan varias rectas secantes con base en éstas y con el apoyo de tu imaginación geométrica observarás que al desplazar el punto $A$ en la dirección del punto $T$, pasa por infinitos puntos; luego entonces, puedes continuar con la construcción de las rectas secantes de manera infinita, siendo ésta una característica de los procesos infinitos, estudiada en el Objeto de Aprendizaje “Procesos infinitos y la noción de límite”; si ni lo has revisado, te invitamos a que lo hagas para que comprendas sus características y su aplicación a problemas que involucran procesos infinitos.
B) La construcción de las rectas secantes como un proceso infinito
El conjunto de los procedimientos geométricos que se realizaron en la construcción de rectas secantes es un proceso infinito ya que puedes continuar con la construcción de una recta secante entre más se aproxima el punto $A$ al punto de tangencia $T$.
Tomando en consideración la exploración y visualización de la construcción realizada, contesta la pregunta: ¿La construcción de las rectas secantes a la gráfica de la función en el punto de tangencia presentada en la figura será un proceso infinito Si/No? La respuesta escríbela en el recuadro y justifícala.
C) Pendiente de la recta tangente
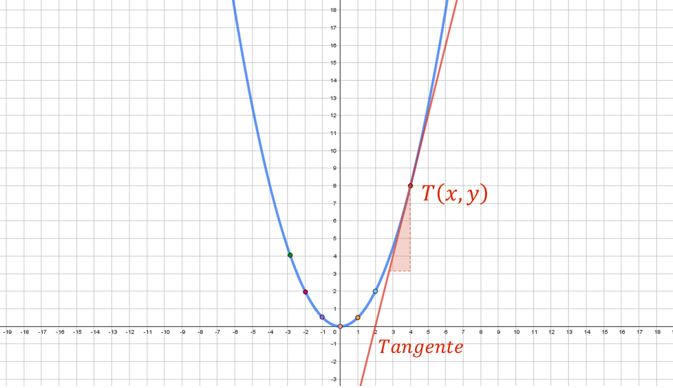
¿Cuál es la pendiente de la recta tangente?
¿Cuál es la pendiente de la recta tangente? Para responder la pregunta debes calcular la pendiente de las rectas secantes y con éstas estimar la pendiente de la recta tangente; recuerda que para calcular la pendiente de una recta que pasa por los puntos de coordenadas $A\left(x_1,y_1\right)$ y $T\left(x_2,y_2\right)$, se utiliza la expresión $m_{AT}=\frac{y_2-y_1}{x_2-x_1}$. En el siguiente video se explican los procesos algebraicos para determinar la pendiente de la recta tangente.
Si quieres aprender más sobre los procedimientos numéricos para obtener la pendiente de la recta tangente, revisa el siguiente recurso GeoGebra.
En los videos y recursos GeoGebra observaste que las rectas secantes tienen como límite la recta tangente cuando el punto $A$ se aproxima al punto de tangencia $T$. Con base en esto y tu intuición matemática, completa la siguiente tabla para evaluar tu comprensión del proceso infinito relacionado con la obtención de la pendiente de la recta tangente mediante las pendientes de las rectas secantes. Escribe en la tabla los datos que faltan, las flechas del penúltimo renglón significan "tiende a" tanto como se quiera.
Para evaluar tu comprensión del tema recuerda que la construcción de las rectas secantes es un proceso infinito, con base en esto contesta la pregunta, ¿cuál es el valor de la pendiente de la recta tangente en el punto de tangencia $T$; escribe la respuesta en los recuadros de color rojo.
D) Notación del límite en la obtención de la pendiente de la recta tangente
Como observaste en los apartados anteriores, cuando el punto $A$ se aproxima al punto de tangencia $T$, las rectas secantes tienen como límite la recta tangente, por lo que las pendientes de las rectas secantes tienen como límite la pendiente de la recta tangente.
La expresión matemática para representar el límite de las rectas secantes y su límite es la siguiente:
Cuando $A\longrightarrow T$, Las rectas secantes $AT \longrightarrow$ la recta tangente en el punto de tangencia $T$
Las pendientes de las rectas secantes $m_{AT}\longrightarrow$ la pendiente de la recta tangente $m_T$.
En la notación, la flecha $(\longrightarrow)$ significa “tiende a”.
De manera formal se utiliza la notación de límite:
$\lim_{A\to T}RectasSecantes AT= Recta\; tangente$
$\lim_{A\to T}{m_{AT}=m_T=4}$