En la sección anterior obtuviste la pendiente de la recta tangente a una función en un punto de tangencia con pendientes de rectas secantes que se construyeron cuando uno de sus puntos se aproxima a éste y la velocidad instantánea de un objeto en un tiempo específico, mediante velocidades promedio en intervalos de tiempo cada vez más pequeños. Con base en esto tenemos las condiciones para el análisis del comportamiento tabular, gráfico y algebraico de una función alrededor de un punto para establecer el concepto del límite de una función.
Análisis de funciones
En este apartado se te presentan algunas funciones que serán analizadas alrededor de un punto, a través de los registros, tabular, gráfico y algebraico con la finalidad de saber a qué valor tiende y su relación con el límite de la función.
Analiza la función $f(x)=x^{3}-3x^{2}+3x+9$ alrededor de $x=5$
En concordancia con tu aprendizaje sobre el estudio de las funciones se plantean las preguntas, ¿la función está definida en $x=5$?, ¿cuál es la gráfica de la función? y ¿existe el límite de la función cuando $x$ tiende a $5$?
El análisis de la función mediante los registros tabular, gráfico y algebraico te permitirá dar respuesta a las preguntas.
Evalúa la función en $x=5$ y contesta lo que se te pide.
Con base en lo anterior, sabemos que la función $f\left(x\right)=x^3-3x^2+3x+9$ está definida en $x=5$, sin embargo, analicemos su comportamiento alrededor $x=5$, mediante los registros tabular, gráfico y algebraico, para establecer a qué valor tiende y dar entada al concepto del límite de una función.
Aspecto tabular
En la tabla siguiente se te presenta la evaluación de la función $f\left(x\right)=x^3-3x^2+3x+9$ para algunos valores de $x$ que se aproximan a $5$, por la izquierda y por la derecha, sin considerar a $5$.
Con base en ambas tablas, realiza lo que se te pide.
Con base en la información presentada en las tablas, realiza la evaluación de la función para el valor de x que se indican en ambas tablas, además, con el apoyo de tu intuición matemática establece a qué valor se aproxima la función por la izquierda y derecha de $x=5$.
Escribe en el recuadro la respuesta de las actividades solicitadas.
Como puede observarse con valores muy cercanos a $x=5$ por la izquierda y por la derecha, se concluye que tiende a $74$.
Aspecto gráfico
Para analizar el comportamiento gráfico de la función $f\left(x\right)=x^3-3x^2+3x+9$ alrededor de $x=5$, se presenta un video como apoyo para tu comprensión.

El recurso GeoGebra se utiliza con el propósito de establecer el comportamiento gráfico de la función mencionada alrededor de $x=5$, esto mediante el análisis gráfico de la función, para que obtengas un primer acercamiento al concepto del límite de una función en un punto especifico de su gráfica que puede estar definida o no en éste.
En el video se presenta la gráfica de la función $f\left(x\right)=x^3-3x^2+3x+9$, presta atención para que comprendas su comportamiento gráfico alrededor de $x=5$.
En concordancia con el video para el análisis de la función alrededor de $x=5$, se observa que la gráfica de la función es una función polinomial de grado tres, al arrastrar el punto de coordenadas $A\left(x,f\left(x\right)\right)$ sobre la función alrededor del valor mencionado; es decir, cuando la abscisa del punto $A$ se aproxima por la izquierda y por la derecha de $x=5$, la ordenada $f(5)$ se aproxima al valor $74$, por lo que el límite de la función es $74$ cuando $x\longrightarrow5$. Con base en esto y en las tablas alrededor de $x=5$ y el recurso GeoGebra, contesta lo que se te pide:
Aspecto algebraico
En concordancia con lo mencionado en el apartado anterior, la gráfica de la función $f\left(x\right)=x^3-3x^2+3x+9$ es una función polinomial de grado tres y como las funciones polinomiales son continuas en todo su dominio (conjunto de los de los números reales $R$), al evaluarla en $x=5$ se obtiene $f\left(5\right)=\left(5\right)^3-3\left(5\right)^2+3\left(5\right)+9=74$, éste valor coincide con la aproximación inferior y superior, por lo que su límite es $74$ cuando $x\longrightarrow5$, y se obtiene con la expresión $\lim_{x \to 5}{\left(x^3-2x^2+3x+9\ \right)=\left(5\right)^3-3\left(5\right)^2+3\left(5\right)+9=74}$.
El análisis de la función $f\left(x\right)=x^3-3x^2+3x+9$ alrededor de $x=5$, a través de los registros tabular, gráfico y algebraico apuntan en la misma dirección, es decir, obtener el límite de la función cuando $x$ tiende al valor especificado, mediante la expresión algebraica $\lim_{x\to 5}{\left(x^3-3x^2+3x+9\ \right)=\left(5\right)^3-3\left(5\right)^2+3\left(5\right)+9=74}$, sin embargo, el límite es un proceso infinito, tal como, lo muestran las aproximaciones inferior y superior alrededor de $x=5$.
Con base en el análisis de la función a través de los registros tabular, gráfico y algebraico en la obtención de su límite nos permite definir de manera intuitiva la continuidad de una función en $x=a$. Una función $f(x)$ es continua en $x=a$ si cumple con las tres condiciones siguientes:
- La función está definida en $x=a$, es decir, $f(a)$ es un número real.
- El límite de la función existe cunado $x\rightarrow a$, es decir, $\lim_{x\to a}{f(x)}$ existe y es un número real.
- El límite de la función es igual a la función evaluada en $x=a$, es decir, $f\left(a\right)=\lim_{x\to a}{f(x)}$.
Como retroalimentación de los conceptos abordados para comprender el concepto del límite de una función, así como, la continuidad de una función continuamos con el análisis de la siguiente función.
Analiza la función $f\left(x\right)=\frac{x^2-9}{x-3}$ alrededor de $x=3$.
En concordancia con tu aprendizaje sobre el estudio de las funciones se te plantean las preguntas, ¿la función está definida en $x=3$?, ¿cuál es la gráfica de la función? y ¿existe el límite de la función cuando $x$ tiende a $3$?
El análisis de la función mediante los registros tabular, gráfico y algebraico te permitirá dar respuesta a las preguntas planteadas.
Intenta la evaluación de la función en x=3 y contesta lo que se te pide, escribe la respuesta de las actividades solicitadas en el recuadro.
Con base en lo anterior, sabemos que la función no está definida en $x=3$, sin embargo, analicemos su comportamiento alrededor $x=3$, mediante los registros tabular, gráfico y algebraico, para establecer a qué valor tiende.
Aspecto tabular
En la tabla siguiente se te presenta la evaluación de la función para algunos valores de $x$ que se aproximan a $3$, por la izquierda y por la derecha, sin considerar a $3$.
Con base en ambas tablas, realiza lo que se te pide.
Con base en la información presentada en las tablas, realiza la evaluación de la función para el valor de $x$ que se indican en ambas tablas, además, con el apoyo de tu intuición matemática establece a qué valor se aproxima la función por la izquierda y derecha de $x=3$. Escribe en el recuadro la respuesta de las actividades solicitadas.
Como observarse, aunque la función no está definida en $x=3$, sin embargo, con valores muy cercanos a éste por la izquierda y por la derecha, se concluye que tiende a $6$.
Aspecto gráfico
Para analizar el comportamiento gráfico de la función $f\left(x\right)=\frac{x^2-9}{x-3}$ alrededor de $x=3$, se presenta un video como apoyo para tu comprensión.

El recurso GeoGebra se utiliza con el propósito de establecer el comportamiento gráfico de la función mencionada alrededor de $x=3$, esto mediante el análisis gráfico de la función, para que avances en la comprensión del concepto del límite de una función en un punto especifico de su gráfica que puede estar definida o no en éste.
En el video se presenta la gráfica de la función $f\left(x\right)=\frac{x^2-9}{x-3}$, presta atención para que comprendas su comportamiento gráfico alrededor de $x=3$.
En concordancia con el video para el análisis de la función alrededor de x=3, se observa que la gráfica de la función es una línea recta con el punto hueco de coordenadas $P\left(3,6\right)$, además, al arrastrar el punto de coordenadas $A\left(x,f\left(x\right)\right)$ sobre la recta alrededor del valor mencionado; es decir, cuando la abscisa del punto A se aproxima por la izquierda y por la derecha de $x=3$, la ordenada $f(3)$ se aproxima al valor $6$, por lo que el límite de la función es $6$ cuando $x\longrightarrow3$.
Con base en esto y en las tablas alrededor de $x=3$ y el recurso GeoGebra, contesta lo que se te pide:
Aspecto algebraico
En concordancia con lo mencionado en el apartado anterior, la gráfica de la función $f\left(x\right)=\frac{x^2-9}{x-3}$ es una línea recta, esto significa que se puede simplificar la expresión $\frac{x^2-9}{x-3}$, puesto que se trata del cociente notable de la diferencia de los cuadrados de dos cantidades entre la diferencia de las cantidades y se factoriza como el producto de binomios conjugados que se obtienen con la raíz cuadrada de los términos cuadráticos, uniéndolos con el signo más y menos, tal como se presenta a continuación $\frac{x^2-9}{x-3}=\frac{\left(x+3\right)\left(x-3\right)}{x-3}=x+3$, para $x\neq3$; consideremos como $g$ la función resultante, es decir, $g\left(x\right)=x+3$, esta función está definida en todo su dominio, en particular, en $x=3$, a diferencia de la función $f\left(x\right)=\frac{x^2-9}{x-3}$.
Cabe mencionar que ambas funciones son idénticas excepto en $x=3$, su gráfica se presenta en la figura y para obtener el límite simplemente se sustituye $x=3$ en la función $g(x)$, mediante la expresión $\lim_{x\to 3}{\left(x+3\right)=3+3=6}$. Esta forma de calcular el límite de la función es adecuada, sin embargo, no olvides que el límite de una función en el valor especifico es un proceso infinito, tal como, lo muestran las aproximaciones por la izquierda y por la derecha del punto mencionado y no debe confundirse como una simple sustitución.
Gráfica de la función $f\left(x\right)=\frac{x^2-9}{x-3}$
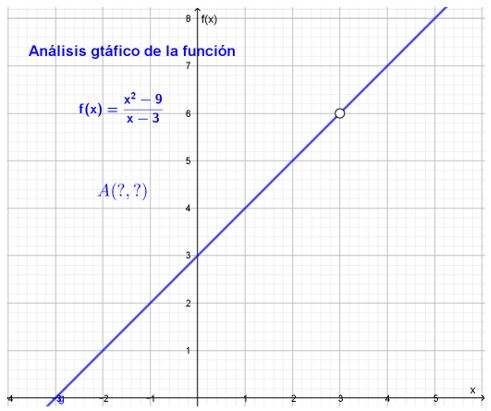
Gráfica de la función $g\left(x\right)=x+3$
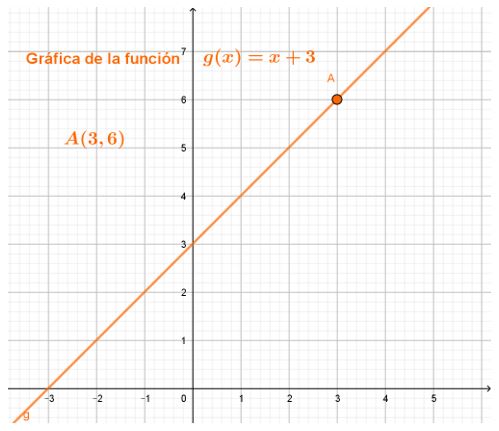
En congruencia con el video, tablas y gráficas, sabemos que cuando $x\longrightarrow3$ por la izquierda y por la derecha, en ambos casos el límite de la función es $6$. Con base en esto, contesta la pregunta.
El análisis de la función $f\left(x\right)=\frac{x^2-9}{x-3}$ alrededor de $x=3$, a través de los registros tabular, gráfico y algebraico apuntan en la misma dirección, es decir, obtener el límite de la función cuando x tiende al punto especificado con la expresión algebraica $\lim_{x\to 3}{\frac{x^2-9}{x-3}=6}$. En este contexto, realiza lo que se te pide.
Con base en el análisis que realizaste a la función mediante los registros tabular, gráfico y algebraico, contesta la siguiente pregunta.
Para continuar con la comprensión del concepto del límite de una función, analicemos la siguiente función.
Analiza la función $f\left(x\right)=\frac{x^3-8}{x-2}$ alrededor de $x=2$.
En concordancia con tu aprendizaje sobre el estudio de las funciones se plantean las siguientes preguntas, ¿la función está definida en $x=2$?, ¿cuál es la gráfica de la función?, ¿existe el límite de la función cuando $x$ tiende a $2$?
El análisis de la función mediante los registros tabular, gráfico y algebraico te permitirá dar respuesta a las preguntas planteadas.
Intenta la evaluación de la función en $x=2$ y contesta lo que se te pide en el recuadro.
Con base en lo anterior, sabemos que la función no está definida en $x=2$, sin embargo, analicemos su comportamiento alrededor de este valor, mediante los registros tabular, gráfico y algebraico, para establecer a qué valor tiende y la relación con su límite.
Aspecto tabular
En las siguientes tablas se presenta la evaluación de la función para algunos valores de $x$ que se aproximan a $2$, por la izquierda y por la derecha.
Con base en ambas tablas, escribe los valores que hacen falta en la tabla:
Con base en la información presentada en las tablas, realiza la evaluación de la función para el valor de $x$ que se indican en éstas, además, con apoyo de tu intuición matemática, especifica a qué valor se aproxima la función por la izquierda y derecha de $x=2$. Escribe la respuesta en la siguiente tabla.
Como puede observarse, aunque la función no está definida en $x=2$, sin embargo, con valores muy cercanos a éste por la izquierda y por la derecha, se concluye que tiende a $12$.
Aspecto gráfico
Para analizar el comportamiento gráfico de la función $f\left(x\right)=\frac{x^3-8}{x-2}$ alrededor de x=2, se presenta un video como apoyo para su comprensión.
El recurso GeoGebra se utiliza con el propósito de comprender el comportamiento gráfico de la función mencionada alrededor de $x=2$, mediante el análisis gráfico de la función, para consolidar el concepto del límite de una función en un punto especifico de su gráfica.
En el video se presenta la gráfica de la función $f\left(x\right)=\frac{x^3-8}{x-2}$, presta atención para que comprendas su comportamiento gráfico, alrededor de $x=2$.
En concordancia con el video para el análisis de la función alrededor de $x=2$, se observa que la gráfica de la función es una parábola con el punto hueco de coordenadas $P\left(2,12\right)$, además, al arrastrar el punto de coordenadas $A$ sobre la parábola alrededor del valor mencionado; es decir, cuando la abscisa de este punto se aproxima por la izquierda y por la derecha de $x=2$, la ordenada $f(2)$ se aproxima a $12$, por lo que el límite de la función cuando $x\longrightarrow2$, $f\left(2\right)\longrightarrow12$.
Con base en las tablas alrededor de $x=2$, el video y el recurso GeoGebra, contesta lo que se te pide:
Aspecto algebraico
En concordancia con lo mencionado en el apartado anterior, la gráfica de la función racional $f\left(x\right)=\frac{x^3-8}{x-2}$ es una parábola con el punto hueco $P\left(2,12\right)$, esto significa que se puede simplificar, puesto que se trata del cociente notable de la diferencia de cubos de dos cantidades entre la diferencia de las cantidades; al factorizar la expresión $\frac{x^3-8}{x-2}=\frac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}=x^2+2x+4$, para $x\neq2$; llamemos $g$ a la función simplificada, es decir, $g\left(x\right)=x^2+2x+4$. Esta función está definida en todo su dominio, en particular, en $x=2$, a diferencia de la función $f\left(x\right)=\frac{x^3-8}{x-2}$; las funciones $f\left(x\right)$ y $g\left(x\right)$ son idénticas, excepto en $x=2$.
La gráfica de ambas funciones, se presentan en la figura; para obtener el límite simplemente se sustituye $x=2$ en la función $g\left(x\right)$, mediante la expresión $\lim_{x\to 2}{\left(x^2+2x+4\right)=\left(2\right)^2+2\left(2\right)+4=12}$. Esta forma de calcular el límite de la función es adecuada, sin embargo, no se te olvide que el límite de una función en el valor especificado es un proceso infinito, tal como, lo muestran las aproximaciones por la izquierda y por la derecha del punto mencionado y no debe confundirse como una simple sustitución.
Gráfica de la función $f\left(x\right)=\frac{x^3-8}{x-2}$
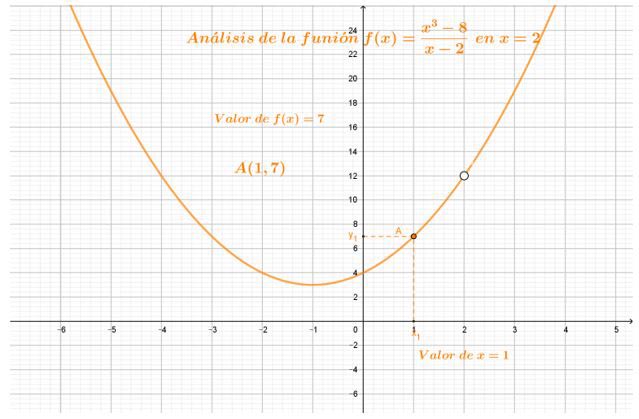
Gráfica de la función $g\left(x\right)=x^2+2x+4$
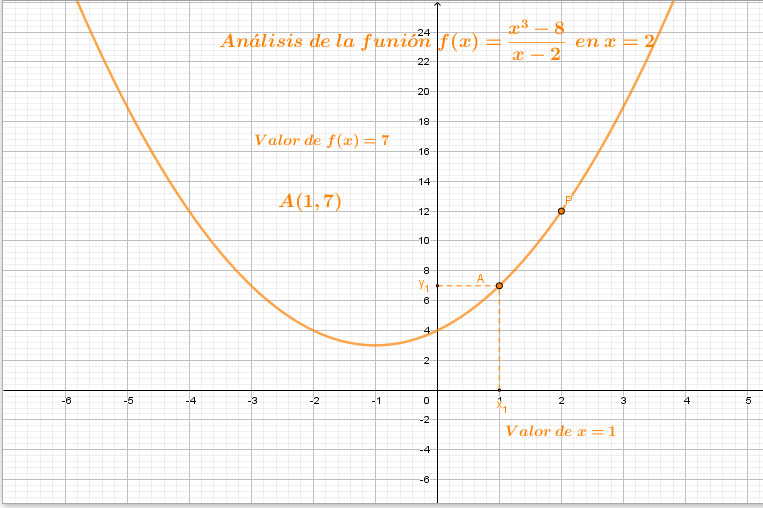
En congruencia con el video, tablas y gráficas, sabemos que cuando $x\longrightarrow2$ por la izquierda y por la derecha, en ambos casos el límite de la función es $12$. Con base en esto, contesta la pregunta.
El análisis de la función $f\left(x\right)=\frac{x^3-8}{x-2}$ alrededor del punto de acumulación $x=2$, a través de los registros tabular, gráfico y algebraico apuntan en la misma dirección, es decir, obtener el límite de la función cuando $x$ tiende al punto especificado con la expresión algebraica $f\left(x\right)=\frac{x^3-8}{x-2}$.
Con base en el análisis que realizaste a la función mediante los registros tabular, gráfico y algebraico, contesta la pregunta y la respuesta escríbela en los recuadros.
En la siguiente pantalla se va a definir el límite de una función.


