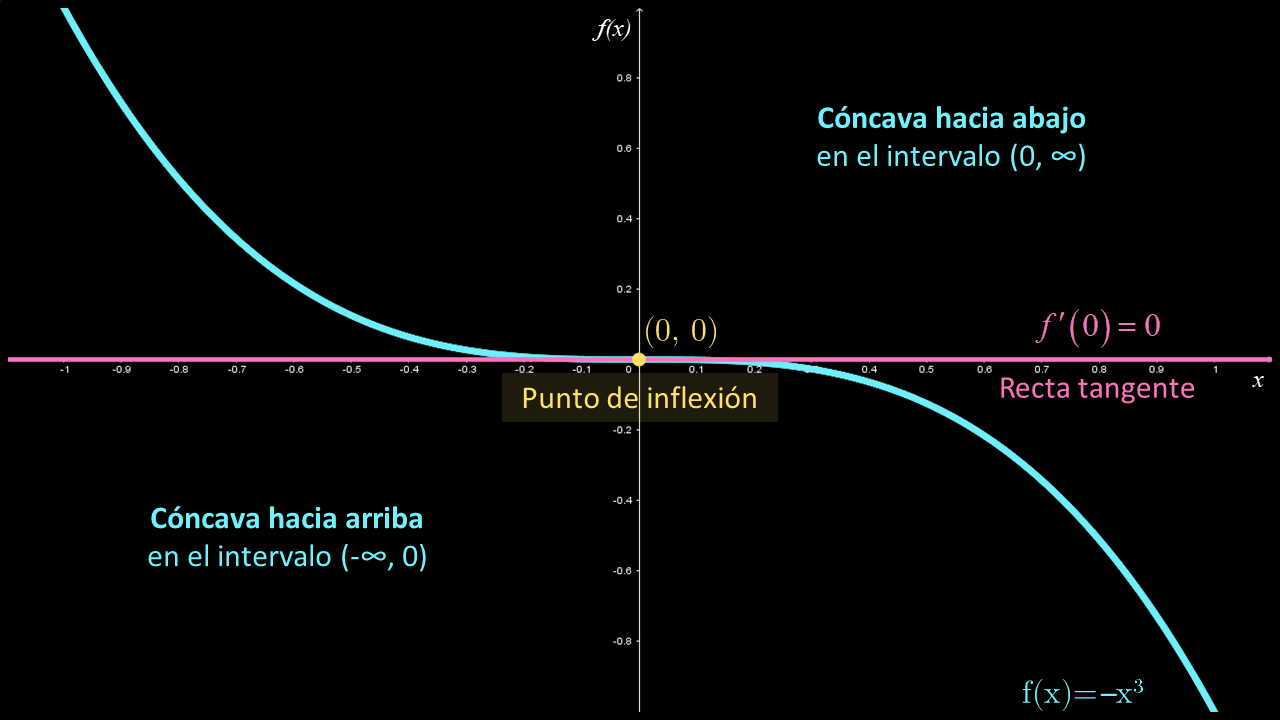
En la siguiente figura se observa que en el punto $\left( {0,0} \right)$ la derivada de la función es cero y, por tanto, la recta tangente es horizontal; dicho punto crítico no presenta valores máximo ni mínimo; sin embargo, en él existe un cambio de concavidad. A este punto crítico se le conoce como punto de inflexión.
En los puntos de inflexión existe cambio de concavidad.
Punto de inflexión
Un punto $P$ sobre una curva $y = f\left( x \right)$ es un punto de inflexión si $f$ es continua en dicho punto y la curva cambia de concavidad en $P$.
Ejemplo
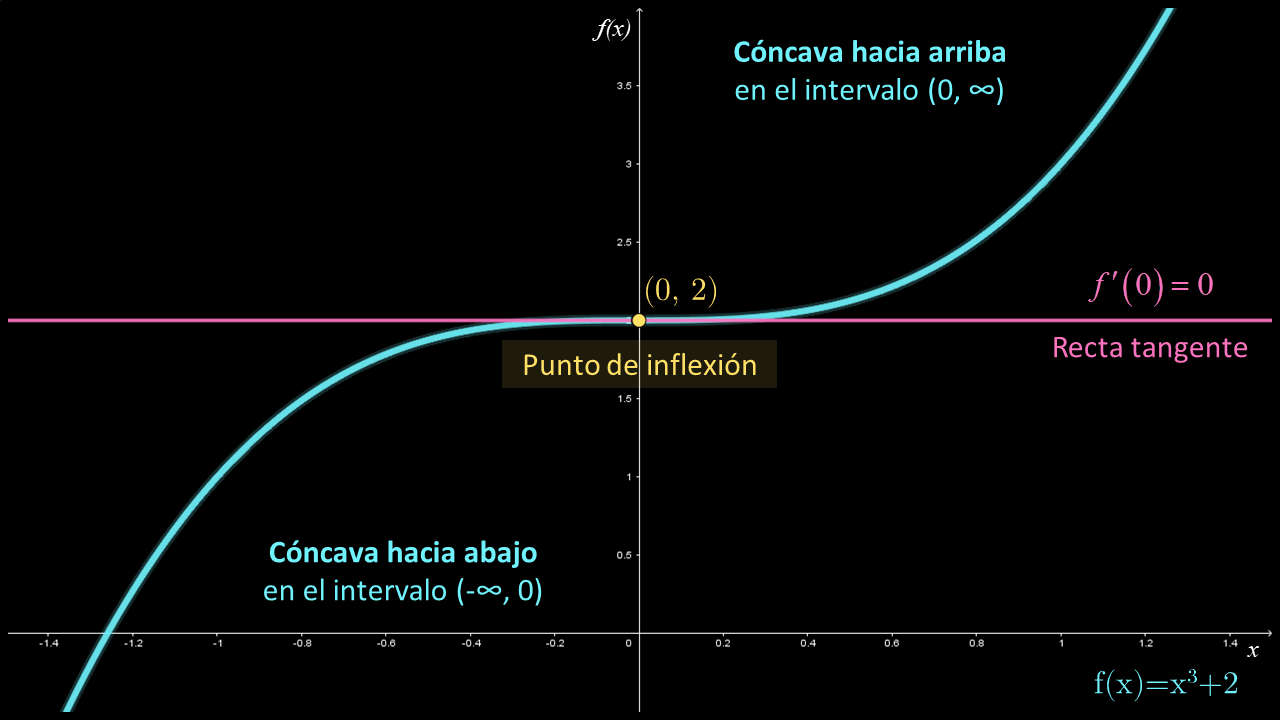
Sea la función $y = {x^3} + 2$, se tiene que su derivada es $f'\left( x \right) = 3{x^2}$ y su segunda derivada es $f''\left( x \right) = 6x$. Al igualar la derivada a cero, $f'\left( x \right) = 3{x^2} = 0$, se determina el número crítico $x = 0$, el cual divide al dominio en los intervalos $\left( { - \infty ,0} \right)$ y $\left( {0,\infty } \right)$. Al analizar ambos intervalos, se encuentra que la función es creciente en todo el dominio, tal como se observa en la tabla.
| Intervalo | Valor de la derivada | $f$ | $f'$ |
|---|---|---|---|
| $\left( { - \infty ,0} \right)$ | $f'\left( { - 1} \right) = 3{\left( { - 1} \right)^2} = 3$ | $+$ | Creciente sobre $\left( { - \infty ,0} \right)$ |
| $\left( {0,\infty } \right)$ | $f'\left( 1 \right) = 3{\left( 1 \right)^2} = 3$ | $+$ | Creciente sobre $\left( {0,\infty } \right)$ |
La tabla anterior muestra que en el número crítico $x = 0$ no se tiene ni un máximo ni un mínimo locales. Para analizar qué sucede en dicho número, así como en su correspondiente punto crítico $\left( {0,2} \right)$, se utiliza el teorema de concavidad:
| Desigualdades | Intervalo donde se cumple la desigualdad | Concavidad de $f$ |
|---|---|---|
| $f''\left( x \right) = 6x < 0$ | $\left( {0,\infty } \right)$ | Cóncava hacia abajo |
| $f''\left( x \right) = 6x > 0$ | $\left( { - \infty ,0} \right)$ | Cóncava hacia arriba |
Con base en tabla anterior, podemos afirmar que:
- La función es cóncava hacia abajo en el intervalo $\left( { - \infty ,0} \right)$
- La función es cóncava hacia arriba en el intervalo $\left( {0,\infty } \right)$
- En el punto $\left( {0,2} \right)$ se tiene un cambio de concavidad; dicho punto es de inflexión.