Para caracterizar los máximos y mínimos locales también es posible utilizar otro método llamado criterio de la segunda derivada.
Criterio de la 2ª derivada
Sea $c$ un número crítico de una función continua $f$, es decir, $f'\left( c \right) = 0$; consideremos que $f''$ es continua cerca de $c$.
a) Si $f''\left( c \right) > 0$, entonces $f$ tiene un mínimo local en $c$.
b) Si $f''\left( c \right) < 0$, entonces $f$ tiene un máximo local en $c$.
c) Si $f''\left( c \right) = 0$, se aplica la prueba de concavidad para determinar si es punto de inflexión, máximo o mínimo.
-
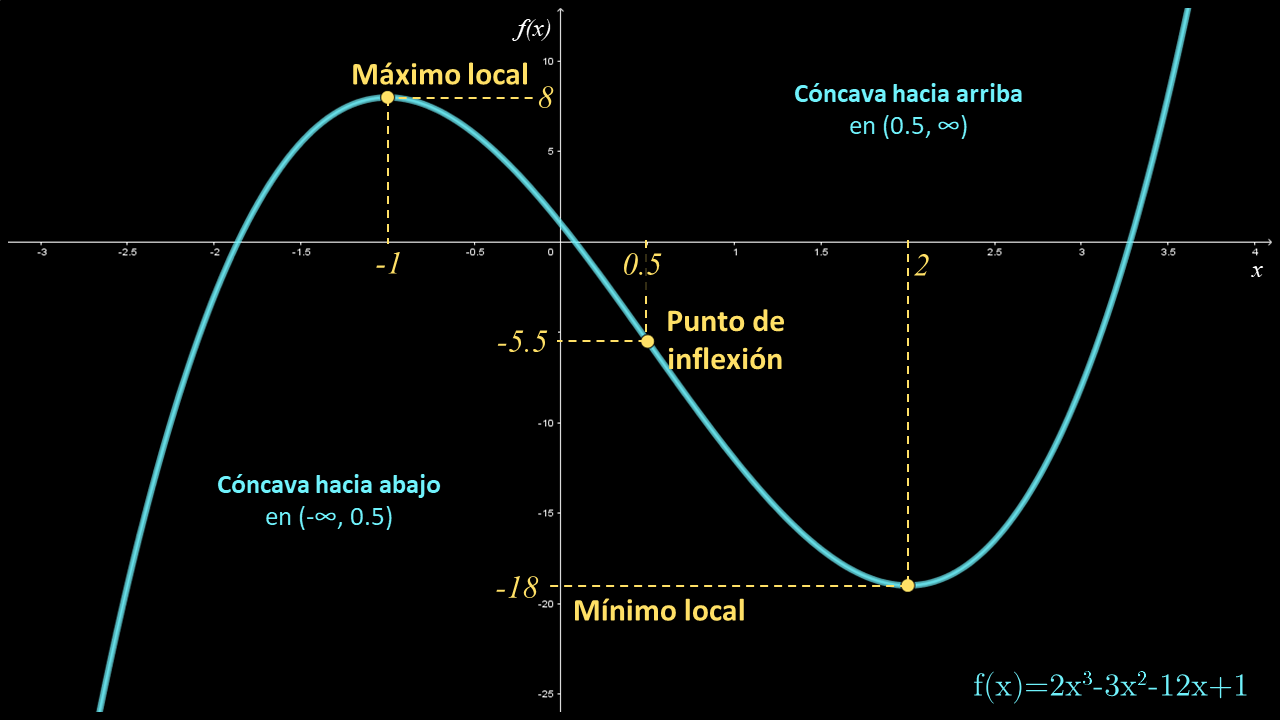
Analiza la función $f\left( x \right) = 2{x^3} - 3{x^2} - 12x + 1$ respecto a valores máximos y mínimos, puntos de inflexión y concavidad; y, a partir de ellos, construye la gráfica.
Primero se determinan la primera y segunda derivadas de $f$:
$\begin{array}{l} f'\left( x \right) = 6{x^2} - 6x - 12 = 6\left( {{x^2} - x - 2} \right)\\ f'\left( x \right) = 6\left( {x - 2} \right)\left( {x + 1} \right)\\ f''\left( x \right) = 12x - 6 = 6\left( {2x - 1} \right) \end{array}$
Después se encuentran los números críticos igualando la primera derivada a cero, es decir, $f'\left( x \right) = 0$:
$f'\left( x \right) = 6\left( {x - 2} \right)\left( {x + 1} \right) = 0$
La igualdad anterior se cumple en los números críticos $x = -1$ y $x = 2$. Para determinar si la función tiene máximos o mínimos, se evalúa $f''$ en los números críticos, de acuerdo con el criterio de la segunda derivada:
Número crítico Valor de $f''$ Signo de $f''$ $f$ $x = - 1$ $f''\left( { - 1} \right) = 6\left( {2\left( { - 1} \right) - 1} \right) = - 18$ $-$ Máximo local en $x = - 1$ $x = 2$ $f''\left( 2 \right) = 6\left( {2\left( 2 \right) - 1} \right) = 18$ $+$ Mínimo local en $x = 2$ A partir de la tabla anterior se puede concluir que:
• Cuando $x = - 1$, se tiene que $f\left( { - 1} \right) = 8$. Por tanto, existe un máximo local en el punto $\left( { - 1,8} \right)$
• Cuando $x = 2$, se tiene que $f\left( 2 \right) = - 18$. Por tanto, existe un mínimo local en el punto $\left( {2, - 18} \right)$.
Ahora, determinamos los puntos de inflexión al igualar la segunda derivada a cero, es decir, $f''\left( x \right) = 0$:
$f''\left( x \right) = 16\left( {2x - 1} \right) = 0$
Al resolver la ecuación se obtiene el número $x = 0.5$, el cual presenta un probable punto de inflexión.
Número $f$ $x = 0.5$ Probable punto de inflexión en $\left( {0.5, - 5.5} \right)$ El número $x = 0.5$ divide al dominio en dos intervalos: $\left( { - \infty ,0.5} \right)$ y $\left( {0.5,\infty } \right)$. Se calcula el signo de la segunda derivada en cada intervalo para determinar si la función es cóncava hacia arriba o hacia abajo en dichos intervalos; para ello, se escoge un número dentro de cada intervalo y se evalúa la segunda deriva en él; el signo del valor de la segunda derivada determina el sentido de la concavidad en el intervalo, según se indica en la siguiente tabla.
Intervalo Valor de $f''$ Signo de $f''$ Concavidad de $f$ $\left( { - \infty ,0.5} \right)$ $f''\left( 0 \right) = 6\left( {2\left( 0 \right) - 1} \right) = - 6$ $-$ Hacia abajo en $\left( { - \infty ,0.5} \right)$ $\left( {0.5,\infty } \right)$ $f''\left( 1 \right) = 6\left( {2\left( 1 \right) - 1} \right) = 6$ $+$ Hacia arriba en $\left( {0.5,\infty } \right)$ A partir de la tabla anterior se puede concluir que:
• El punto $\left( {0.5, - 5.5} \right)$ es un punto de inflexión ya que en él la curva cambia de cóncava hacia abajo a cóncava hacia arriba.
Con el análisis de la función, se obtiene la gráfica como se muestra a continuación:
-
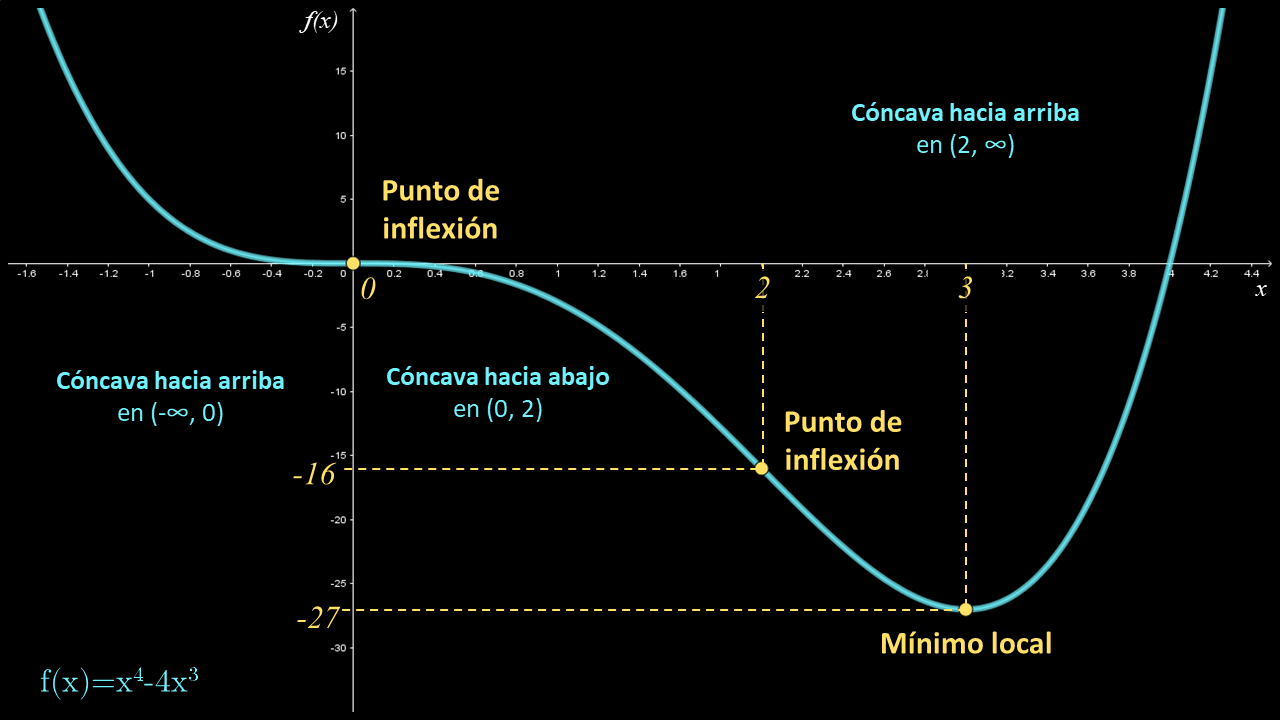
Analiza la función $f\left( x \right) = {x^4} - 4{x^3}$ respecto a valores máximos y mínimos, puntos de inflexión; y a partir de ellos, construye la gráfica.
Se inicia determinando la primera y segunda derivadas de $f$:
$\begin{array}{l} f'\left( x \right) = 4{x^3} - 12{x^2} = 4{x^2}\left( {x - 3} \right)\\ f''\left( x \right) = 12{x^2} - 24x = 12x\left( {x - 2} \right) \end{array}$
Después se encuentran los números críticos igualando la derivada a cero, es decir, $f'\left( x \right) = 0$:
$f'\left( x \right) = 4{x^2}\left( {x - 3} \right) = 0$
La igualdad anterior se cumple en los números críticos $x = 0$ y $x = 3$. Para determinar si la función tiene máximos o mínimos, se evalúa $f''$ en los números críticos para utilizar el criterio de la segunda derivada.
Número crítico Valor de $f''$ Signo de $f''$ $f$ $x = 0$ $f''\left( 0 \right) = 12\left( 0 \right)\left( {\left( 0 \right) - 2} \right) = 0$ Probable punto de inflexión en $x = 0$ $x = 3$ $f''\left( 3 \right) = 12\left( 3 \right)\left( {\left( 3 \right) - 2} \right) = 36$ $+$ Mínimo local en $x = 3$ A partir de la tabla anterior se puede concluir que:
• Cuando $x = 0$, se tiene que $f\left( 0 \right) = 0$. Por tanto, existe un probable punto de inflexión en $\left( {0,0} \right)$.
• Cuando $x = 3$, se tiene que $f\left( 3 \right) = -27$. Por tanto, existe un mínimo local en el punto $\left( {3, - 27} \right)$.
Ahora determinamos los probables puntos de inflexión al igualar la segunda derivada a cero, es decir, $f''\left( x \right) = 0$:
$f''\left( x \right) = 12x\left( {x - 2} \right) = 0$
Al resolver la ecuación se obtienen los números $x = 0$ y $x = 2$; que presentan probables puntos de inflexión.
Número $f$ $x = 0$ Probable punto de inflexión en $\left( {0,0} \right)$ $x = 2$ Probable punto de inflexión en $\left( {2, - 16} \right)$ Los números $x = 0$ y $x = 2$ dividen al dominio en los intervalos: $\left( { - \infty ,0} \right)$, $\left( {0,2} \right)$ y $\left( {2,\infty } \right)$. Se calcula el signo de la segunda derivada en cada intervalo para determinar si la función es cóncava hacia arriba o hacia abajo en dichos intervalos; para ello, se escoge un número dentro de cada intervalo y se evalúa la segunda deriva en él; el signo del valor de la segunda derivada determina el sentido de la concavidad en el intervalo, según se indica en la siguiente tabla.
Intervalo Valor de $f''$ Signo de $f''$ Concavidad de $f$ $\left( { - \infty ,0} \right)$ $f''\left( { - 1} \right) = 12\left( { - 1} \right)\left( {\left( { - 1} \right) - 2} \right) = 36$ $+$ Hacia arriba en $\left( { - \infty ,0} \right)$ $\left( {0,2} \right)$ $f''\left( 1 \right) = 12\left( 1 \right)\left( {\left( 1 \right) - 2} \right) = - 12$ $-$ Hacia abajo en $\left( {0,2} \right)$ $\left( {2,\infty } \right)$ $f''\left( 3 \right) = 12\left( 3 \right)\left( {\left( 3 \right) - 2} \right) = 36$ $+$ Hacia arriba en $\left( {2,\infty } \right)$ A partir de la tabla anterior se puede concluir que:
• El punto $\left( {0,0} \right)$ es un punto de inflexión ya que en él la curva cambia de cóncava hacia arriba a cóncava hacia abajo.
• El punto $\left( {2, - 16} \right)$ es un punto de inflexión ya que en él la curva cambia de cóncava hacia abajo a cóncava hacia arriba.
Con el análisis de la función, se obtiene la gráfica como se muestra a continuación:
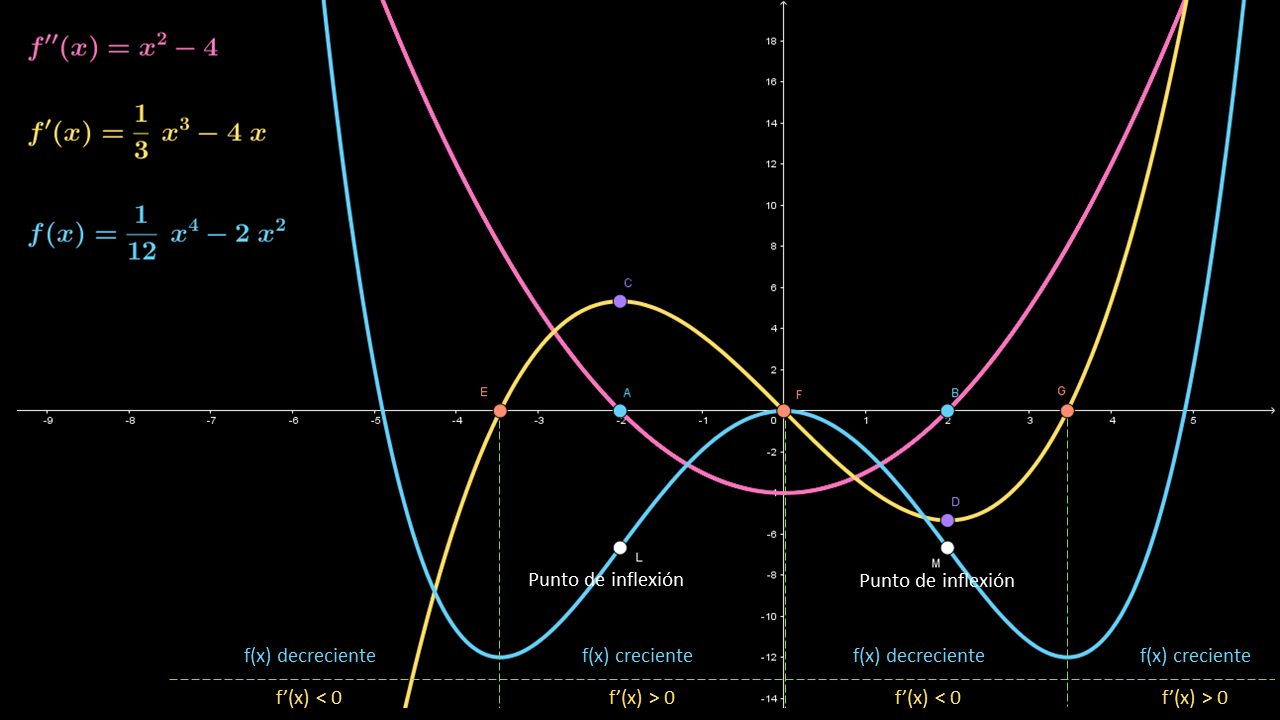
Graficando la función f(x) a partir de sus dos primeras derivadas
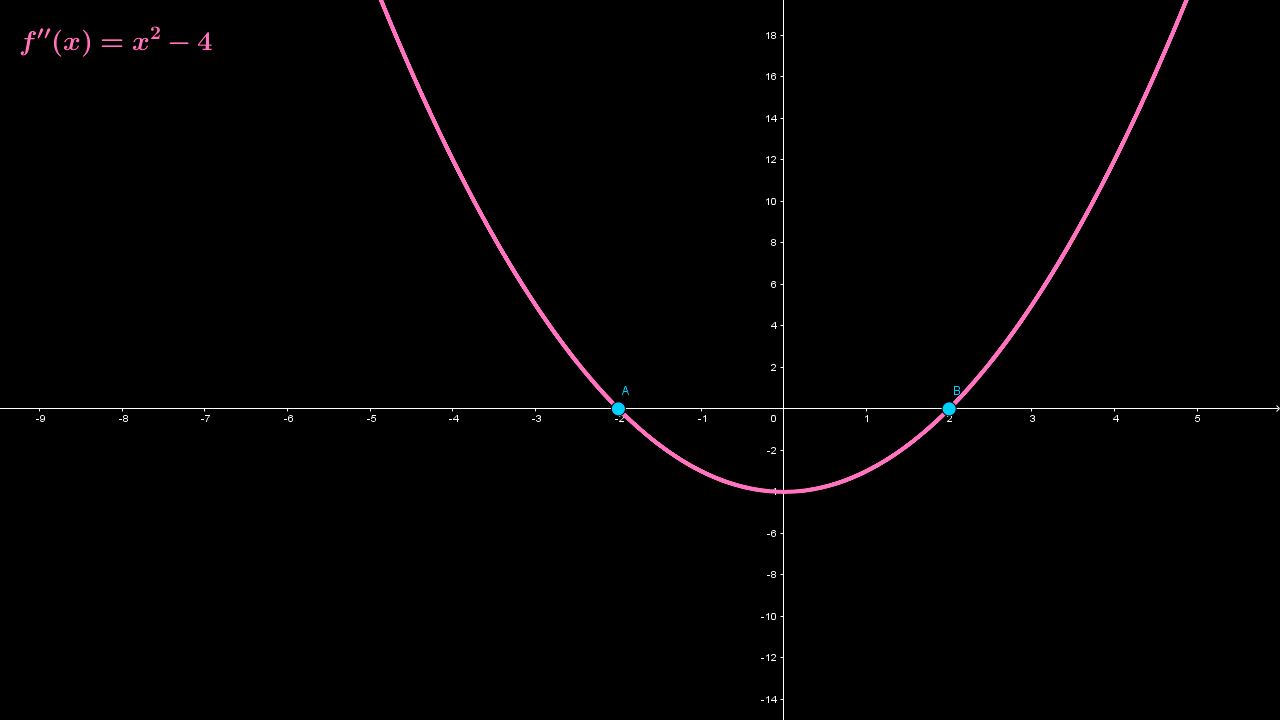
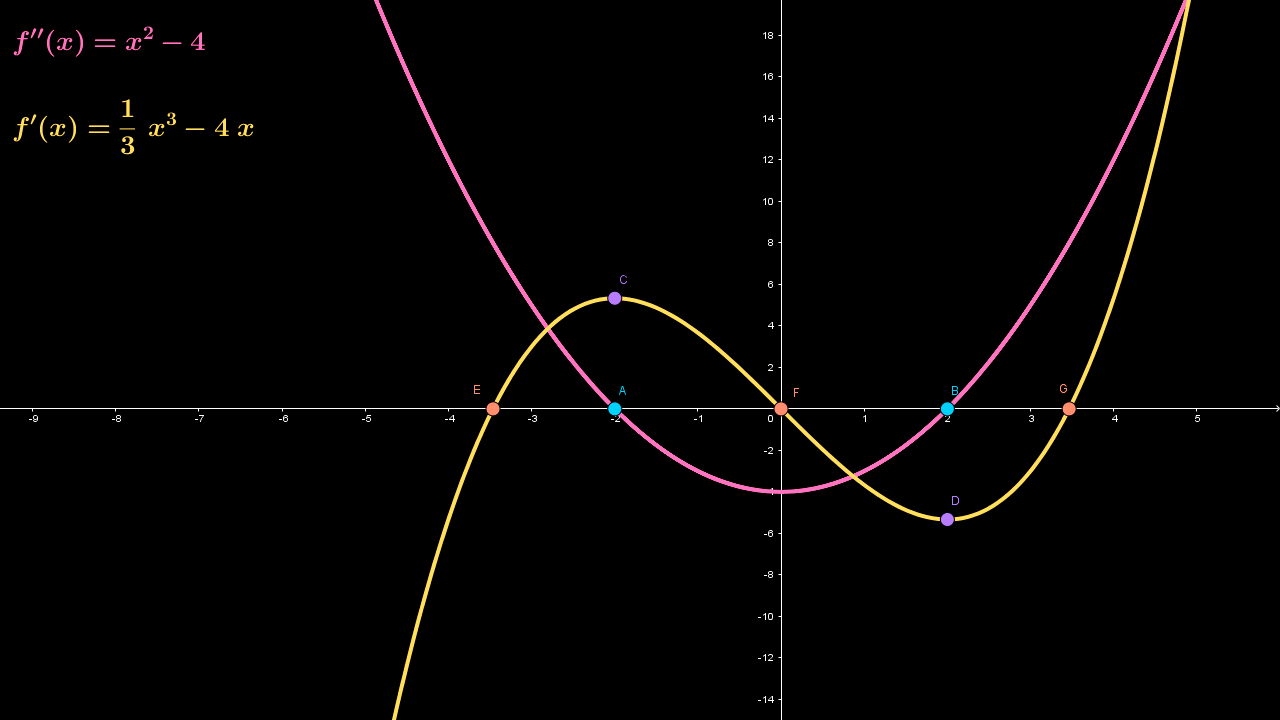
Construye la gráfica de la función $f\left( x \right)$ con base en la información de la gráfica de la primera y segunda derivadas, mostradas en las siguientes figuras.
De la gráfica de la segunda derivada $f''\left( x \right) = {x^2} - 4$, se tiene que ésta es positiva en el intervalo $\left( { - \infty , - 2} \right)$, negativa en el intervalo $\left( { - 2,2} \right)$ y positiva en el intervalo $\left( {2,\infty } \right)$. Además, la gráfica de la primera derivada $f'\left( x \right)$ es creciente, decreciente y creciente en los intervalos mencionados, respectivamente.
También se tiene que -2 y 2 son números críticos de la segunda derivada de la función $f\left( x \right)$. Del mismo modo, $f''\left( x \right) = {x^2} - 4$ es decreciente en el intervalo $\left( { - \infty , 0} \right)$ y creciente en el intervalo $\left( {0,\infty } \right)$, por lo que la primera derivada $f'\left( x \right)$ tiene un punto de inflexión en $\left( { 0,0} \right)$.
Los números críticos de la primera derivada $f'\left( x \right)$ son los puntos $E$, $F$ y $G$ y representan máximos o mínimos de la función $f\left( x \right)$. Por otra parte, los números críticos $A$ y $B$ de la segunda derivada $f''\left( x \right)$ representan puntos de inflexión de la función $f\left( x \right)$.
En la tabla se indica el signo de la primera derivada $f'\left( x \right)$ en los intervalos que se presentan y se especifica si la función $f\left( x \right)$ es creciente o decreciente.
| Intervalos | ||||
|---|---|---|---|---|
| Derivada $f'\left( x \right)$ | $\left( { - \infty ,E} \right)$ | $\left( {E,F} \right)$ | $\left( {F,G} \right)$ | $\left( {G,\infty } \right)$ |
| Signo | $-$ | $+$ | $-$ | $+$ |
| Función $f\left( x \right)$ | Decreciente | Creciente | Decreciente | Creciente |
Con base en la información de la tabla, concluimos que la gráfica de la función $f\left( x \right)$ es decreciente en el intervalo $\left( { - \infty ,E} \right)$, puesto que $f'\left( x \right)<0$; creciente en el intervalo $\left( {E,F} \right)$, puesto que $f'\left( x \right)>0$; decreciente en el intervalo $\left( {F,G} \right)$, puesto que $f'\left( x \right)<0$; y creciente en el intervalo $\left( {G,\infty } \right)$, puesto que $f'\left( x \right)>0$.
Además, la gráfica de la función $f\left( x \right)$ es cóncava hacia arriba en el intervalo $\left( { - \infty ,A} \right)$, puesto que $f''\left( x \right) = {x^2} – 4>0$; cóncava hacia abajo en el intervalo $\left( {A,B} \right)$, ya que $f''\left( x \right) = {x^2} – 4<0$; y cóncava hacia arriba en el intervalo $\left( {B,\infty } \right)$, puesto que $f''\left( x \right) = {x^2} – 4>0$.
Como el signo de la primera derivada $f'\left( x \right)$ pasa de menos a más en $E$, la función $f\left( x \right)$ tiene un mínimo relativo en $E$; máximo relativo en $F$, puesto que el signo de la derivada pasa de más a menos en $F$; y mínimo relativo en $G$, dado que el signo de la primera derivada pasa de menos a más.