Determinar los valores máximos y mínimos de una función te permitirá optimizar los procesos o los resultados en diversas situaciones prácticas, tanto académicas, sociales, económicas como profesionales. Por ejemplo, las empresas manufactureras desean maximizar las utilidades y minimizar los insumos; la industria petrolera desea minimizar los riesgos derivados durante la extracción de petróleo y maximizar el volumen de extracción; los investigadores del área de las energías renovables buscan maximizar la eficiencia energética de paneles solares, generadores hidráulicos y otras fuentes de energía limpia; las instituciones educativas desean maximizar el egreso y disminuir la deserción escolar; los gobiernos buscan disminuir la pobreza y maximizar el producto interno bruto.
En esta sección revisarás problemas de maximización de áreas, volúmenes y beneficios; así como de minimización de distancias, tiempos y costos.
-
Producto máximo
Determina dos números positivos cuya suma sea $70$ y su producto sea máximo.
Sean $x$ y $y$ los números positivos, la restricción para la suma se puede expresar como:
$x + y = 70$
Y la condición para la multiplicación se expresa como:
$x \cdot y = P$
donde $P$ es la función producto para la que se está buscando su valor máximo. De la primera ecuación se tiene que $y = 70 - x$, que al sustituirse en la expresión para el producto se tiene que:
$P = x \cdot \left( {70 - x} \right) = - {x^2} + 70x$
Se deriva $P$ para encontrar el producto máximo
$\begin{array}{l} P' = - 2x + 70\\ P'' = - 2 \end{array}$
Observa que la segunda derivada es negativa para toda $x$ en el dominio de $P$.
Después se encuentran los números críticos igualando la primera derivada a cero, es decir, $P'\left( x \right) = 0$:
$P'\left( x \right) = - 2x + 70 = 0$
La igualdad anterior se cumple en el número crítico $x = 35$. Para determinar si la función $P$ tiene un máximo o mínimo, se evalúa $P''$ en el número crítico, de acuerdo con el criterio de la segunda derivada:
Número crítico Valor de $P''$ Signo de $P''$ $P$ $x = 35$ $P''\left( {35} \right) = - 2$ $-$ Máximo local en $x = 35$ A partir de la tabla anterior y las restricciones iniciales, se puede concluir que:
• Cuando $x = 35$, se tiene que $y = 70 - \left( {35} \right) = 35$.
• El producto máximo $P$ se tiene cuando $x = 35$ y $y = 35$; el valor máximo es
$P = \left( {35} \right)\left( {35} \right) = 1225$.
-
Volumen máximo
Si el reglamento del servicio postal establece que, para enviar un paquete por correo, el perímetro de la base más la altura de no debe exceder 108 centímetros ¿Cuál es el volumen máximo de un paquete rectangular con dos lados cuadrados que puede enviarse?
Sean $x$ y $y$ las dimensiones de la base de la caja; y x la longitud de la altura. La restricción del perímetro para el envío de paquetes se puede escribir como:
$3x + 2y = 108$
Y la expresión para el volumen es:
$V = x \cdot x \cdot y = {x^2} \cdot y$
donde $V$ es la función volumen para la que se está buscando su valor máximo.
De la primera ecuación se tiene que $y = 54 - \frac{3}{2}x$, que al sustituirse en la expresión para el volumen se tiene que:
$V = {x^2} \cdot \left( {54 - \frac{3}{2}x} \right) = 54{x^2} - \frac{3}{2}{x^3}$
Se deriva $V$ para encontrar el volumen máximo:
$\begin{array}{l} V' = 108x - \frac{9}{2}{x^2} = x\left( {108 - \frac{9}{2}x} \right)\\ V'' = 108 - 9x \end{array}$
Después se encuentran los números críticos igualando la primera derivada a cero, es decir, $V'\left( x \right) = 0$:
$V'\left( x \right) = x\left( {108 - \frac{9}{2}x} \right) = 0$
La igualdad anterior se cumple en los números críticos $X=0$ y $X=24$. Para determinar si la función $V$ tiene un máximo o mínimo, se evalúa $V''$ en los números críticos, de acuerdo con el criterio de la segunda derivada:
Número crítico Valor de $V''$ Signo de $V''$ $V$ $x = 0$ $V''\left( 0 \right) = 108$ $+$ Máximo local en $x = 0$ $x = 24$ $V''\left( {24} \right) = - 108$ $-$ Máximo local en $x = 24$ A partir de la tabla anterior y las restricciones iniciales, se puede concluir que:
• Se tiene un volumen mínimo cuando $x = 0$ cm; lo cual es obvio debido a que se estaría considerando una caja con algunas dimensiones nulas (lo cual carece de sentido físico).
• Se tiene un volumen máximo cuando $x = 24$ cm y $y = 54 - \frac{3}{2}\left( {24} \right) = 18$ cm. El volumen máximo es
$V = {x^2} \cdot y = {24^2} \cdot \left( {18} \right) = 10368$ cm3.
-
Área máxima
Se tiene una malla de 1200 m de largo con la que se desea cercar un jardín rectangular ¿Cuáles son las dimensiones que debe tener el terreno para cercar la mayor área posible?
Sean $x$ y $y$ las dimensiones del jardín, la restricción por la longitud de la malla es:
$2x + 2y = 1200$
Y la expresión para el área es:
$A = x \cdot y$
donde $A$ es la función área para la que se está buscando su valor máximo. Para este problema es necesario encontrar una relación entre las variables $x$ y $y$ para que la función área quede en términos de una de ellas.
De la primera ecuación se tiene que $y = 600 - x$, que al sustituirse en la expresión para el área se tiene que:
$A = x \cdot \left( {600 - x} \right) = 600x - {x^2}$
Se deriva $A$ para encontrar el área máxima:
$\begin{array}{l} A' = 600 - 2x\\ A'' = - 2 \end{array}$
Después se encuentran los números críticos igualando la primera derivada a cero, es decir, $A'\left( x \right) = 0$:
$A'\left( x \right) = 600 - 2x = 0$
La igualdad anterior se cumple el número crítico $x = 300$. Para determinar si la función $A$ tiene un máximo o mínimo, se evalúa $A''$ en el número crítico, de acuerdo con el criterio de la segunda derivada:
Número crítico Valor de $A''$ Signo de $A''$ $A$ $x = 300$ $A''\left( {300} \right) = - 2$ $-$ Máximo local en $x = 300$ A partir de la tabla anterior y las restricciones iniciales, se puede concluir que:
• Se tiene un área máxima cuando $x = 300$ m;
• Se tiene un área máxima cuando $x = 300$ m y $y = 600 - \left( {300} \right) = 300$ m. El área máxima es
$A = x \cdot y = \left( {300} \right) \cdot \left( {300} \right) = 9000$ m2.
-
Volumen máximo
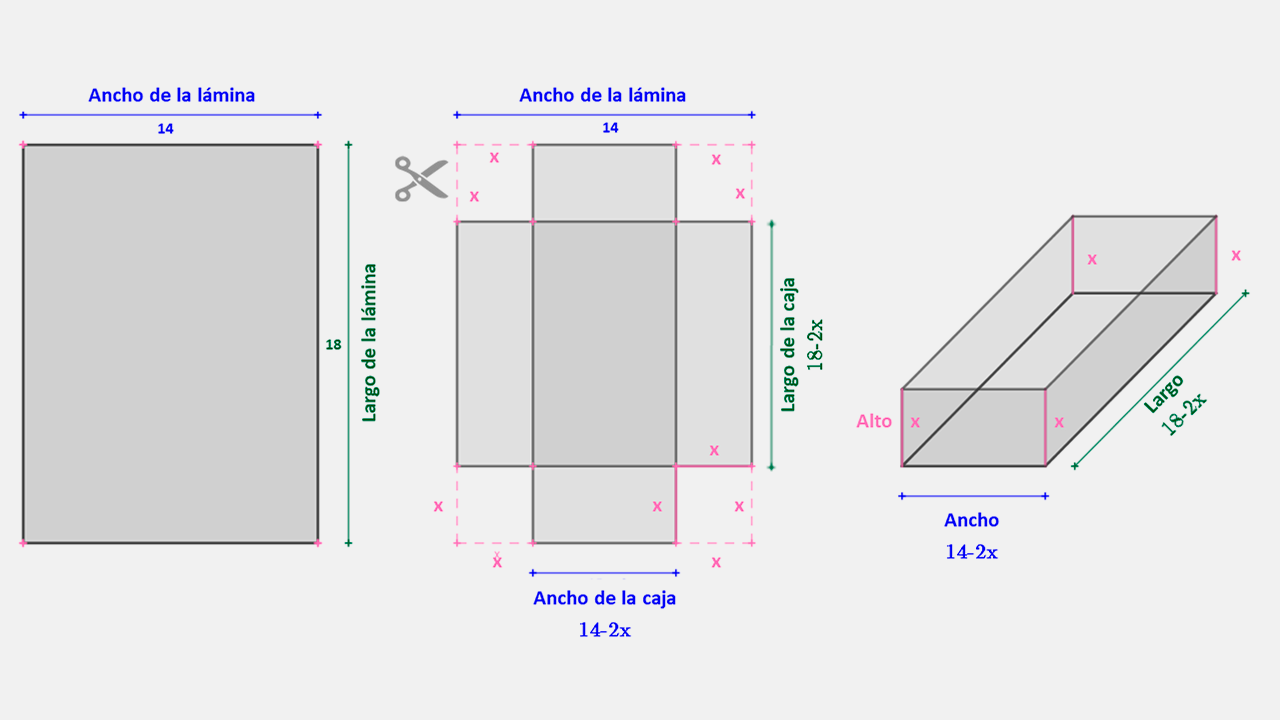
Se construirá una caja sin tapa con una lámina rectangular de 18 centímetros de largo y 14 centímetros de ancho. Para ello, se cortan cuadrados congruentes en las cuatro esquinas del cartón; luego se doblan las pestañas resultantes hacia arriba ¿Cuáles son las dimensiones de la caja que permiten el máximo volumen?
En la figura se expresa el modelo geométrico de construcción de la caja, indicando sus dimensiones en términos de $x$.
Las dimensiones de la caja se pueden expresar en términos de x de la siguiente manera:
Dimensión Expresión algebraica Justificación Altura $x$ Es la longitud de un lado del cuadrado de corte Ancho $14-2x$ Los $14$ cm iniciales menos $2x$ por los cortes de los dos cuadrados en las esquinas Largo $18-2x$ Los $18$ cm iniciales menos $2x$ por los cortes de los dos cuadrados en las esquinas Considerando las expresiones algebraicas en términos de $x$ para el alto, ancho y largo de la caja, y utilizando la fórmula del volumen, se obtiene que la expresión para el volumen es:
$\begin{array}{l} V\left( x \right) = x\left( {14 - 2x} \right)\left( {18 - 2x} \right)\\ V\left( x \right) = 4{x^3} - 64{x^2} + 252x \end{array}$
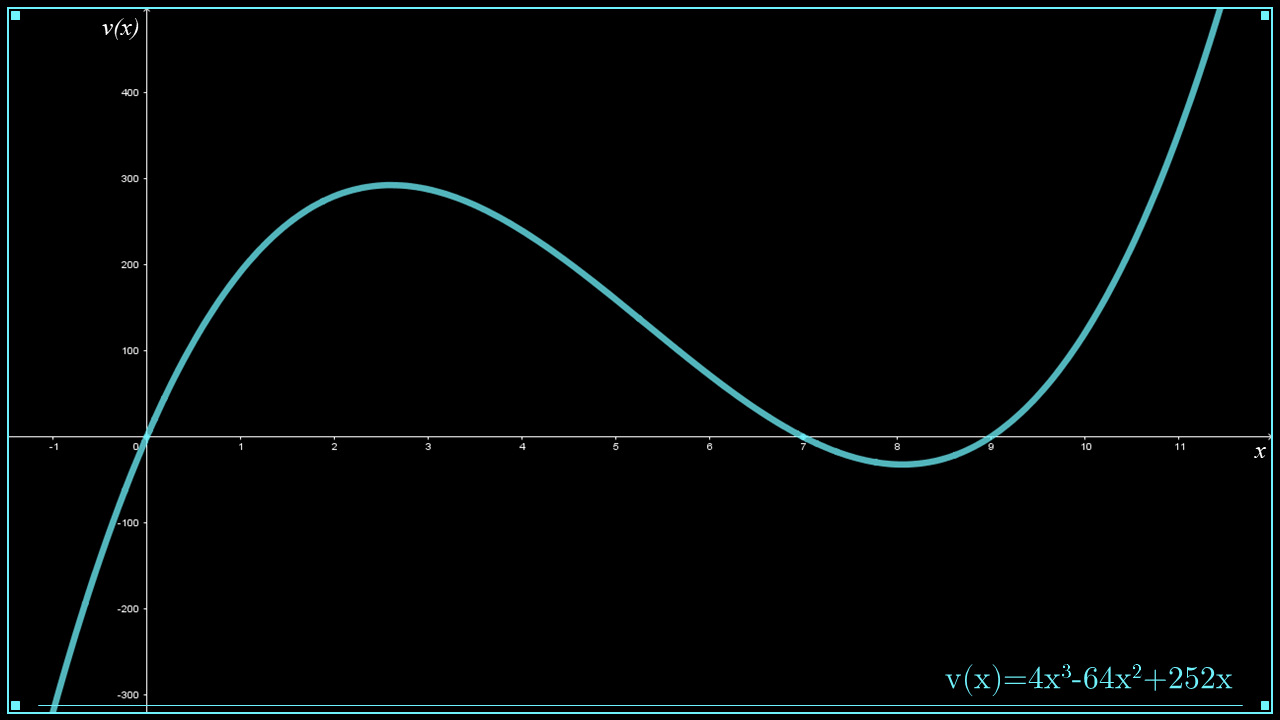
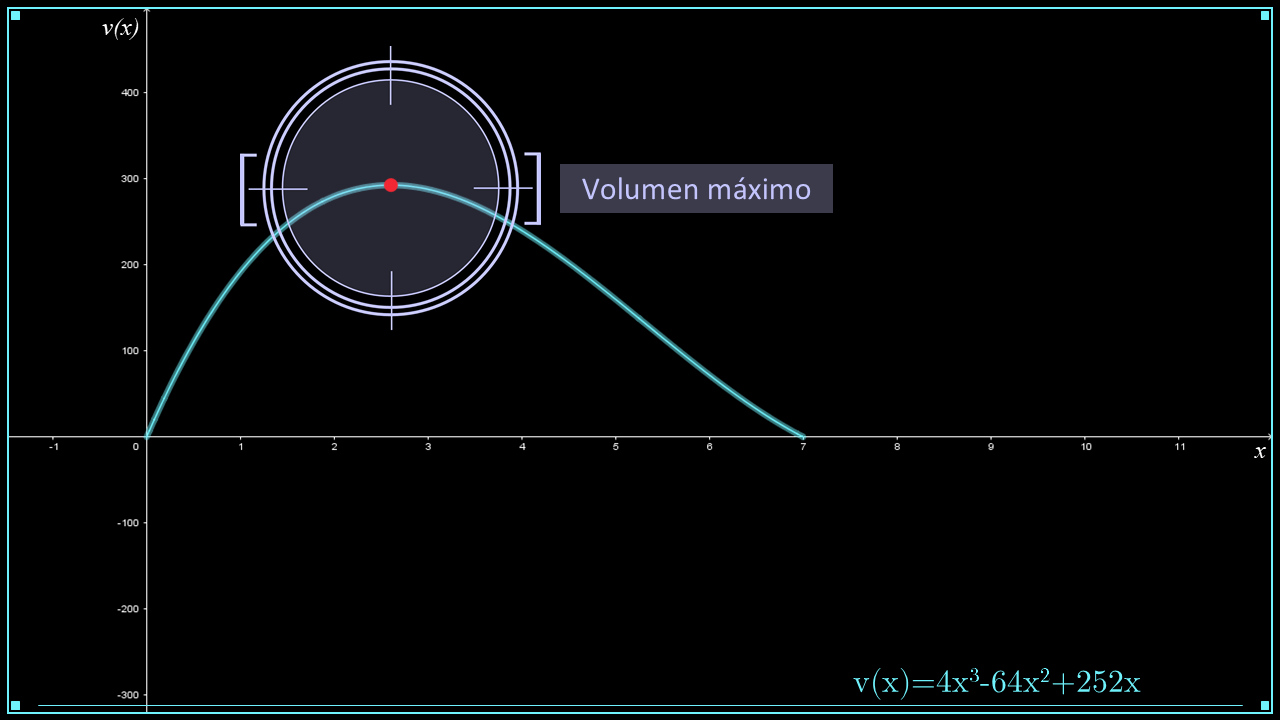
En la siguiente figura se muestra la gráfica de la función $V\left( x \right) = 4{x^3} - 64{x^2} + 252x$, donde el eje horizontal representa la altura $x$ de la caja y el eje vertical el volumen $V\left( x \right) $.
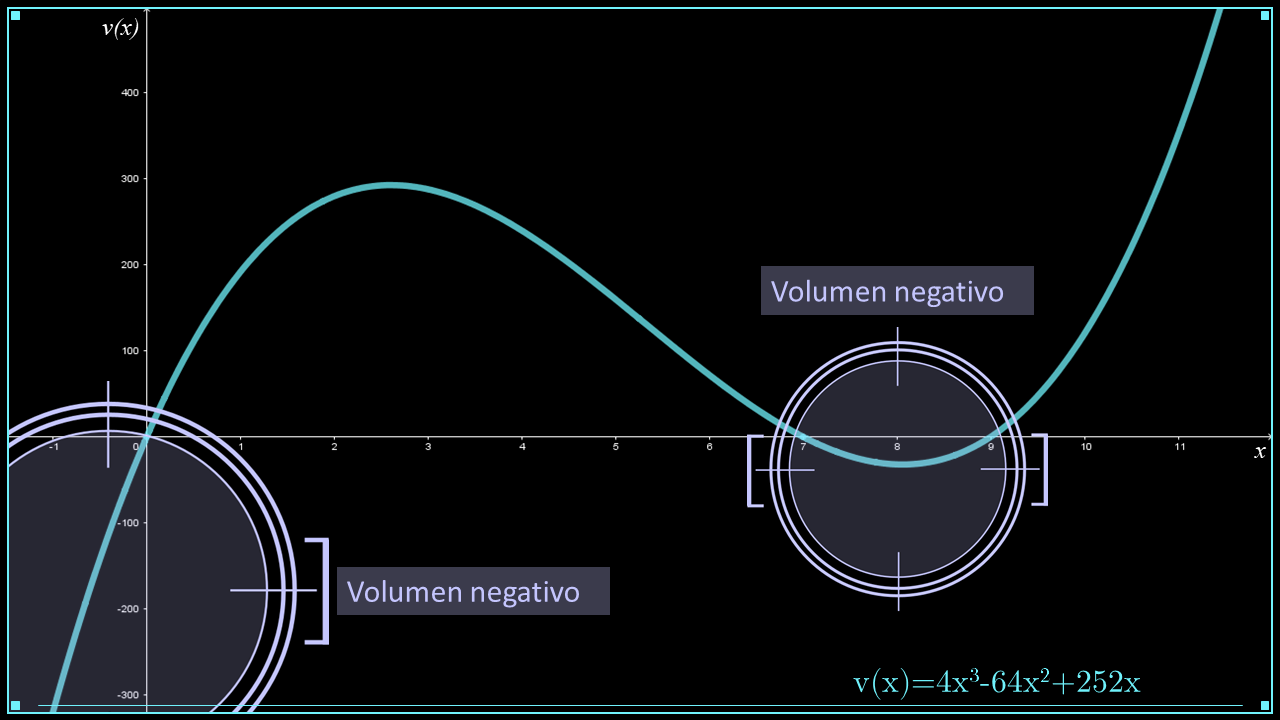
Observa que la gráfica indica regiones con un volumen negativo, lo cual no es posible físicamente. Por ello debemos definir el dominio de la función en el contexto del problema.Para definir el dominio de la función en el contexto del problema, debes tener en cuenta las siguientes tres consideraciones para la construcción de la caja:
Dimensión Expresión algebraica Condición Altura $x$ $x \ge 0$ Ancho $14-2x$ $14 - 2x \ge 0$ Largo $18-2x$ $18 - 2x \ge 0$ La primera condición establece que el tamaño del corte es mayor o igual a cero:
$x \ge 0$
De la segunda condición, al despejar x en la desigualdad, se obtiene que:
$x \le 7$
Mientras que, de la tercera condición, al despejar $x$ en la desigualdad, se obtiene que:
$x \le 9$
En consecuencia, tomando en cuenta las tres condiciones anteriores, es posible afirmar que el dominio de la función en el contexto del problema es:
$x \in \left[ {0,7} \right]$
O bien,
$0 \le x \le 7$
Considerando el tamaño de la lámina original, no es posible hacer los cortes mencionados con longitudes fuera del dominio; es decir, es imposible cortar cuatro cuadrados congruentes con lados menores a $0$ cm ni mayores a $7$ cm.
En la gráfica se muestra que, en el dominio de la función, existe un valor $x$ para la altura que implica un volumen máximo $V'\left( x \right)$.
Se deriva $V$ para encontrar el volumen máximo
$\begin{array}{l} V'\left( x \right) = 12{x^2} - 128x + 252\\ V''\left( x \right) = 24x - 128 \end{array}$
Después se encuentran los números críticos igualando la derivada a cero, es decir, $V'\left( x \right) = 0$:
$V'\left( x \right) = 12{x^2} - 128x + 252 = 0$
Utilizando la fórmula general encontramos que la igualdad se cumple en los números críticos $x \approx 2.605$ y $x \approx 8.062$; sin embargo, el segundo número está fuera del dominio de la función, por lo que consideraremos sólo al primero. Para determinar si la función $V$ tiene un máximo o mínimo en $x \approx 2.605$, se evalúa este valor en $V''$, de acuerdo con el criterio de la segunda derivada:
Número crítico Valor de $V''$ Signo de $V''$ $V$ $x \approx 2.605$ $V''\left( {2.605} \right) = - 65.48$ $-$ Máximo local en $x \approx 2.605$ A partir de la tabla anterior y las restricciones iniciales, se puede concluir que:
• Se tiene un volumen máximo cuando $x \approx 2.605$ cm. El volumen máximo es
$V\left( {2.605} \right) = 4{\left( {2.605} \right)^3} - 64{\left( {2.605} \right)^2} + 252\left( {2.605} \right)$
$V\left( {2.605} \right) = 292.865$ cm3
En la siguiente tabla se indican las dimensiones de la caja que corresponden al volumen máximo.
Dimensión Expresión algebraica Valor [cm] Altura $x$ $2.605$ Ancho $14-2x$ $8.79$ Largo $18-2x$ $12.79$