Área máxima
Se tiene una malla de 2000 m de largo con la que se desea cercar un jardín rectangular que colinda con un río. Determina las dimensiones que debe tener el terreno para cercar la mayor área posible. Selecciona las respuestas correctas.
Sean $x$ y $y$ el ancho y largo, respectivamente, para las dimensiones del jardín.
1. La restricción para colocar la malla alrededor del jardín es:
2. La expresión para el área es:
3. La primera deriva del área es:
4. La segunda deriva del área es:
5. Los valores que permiten un área máxima son:
Volumen máximo
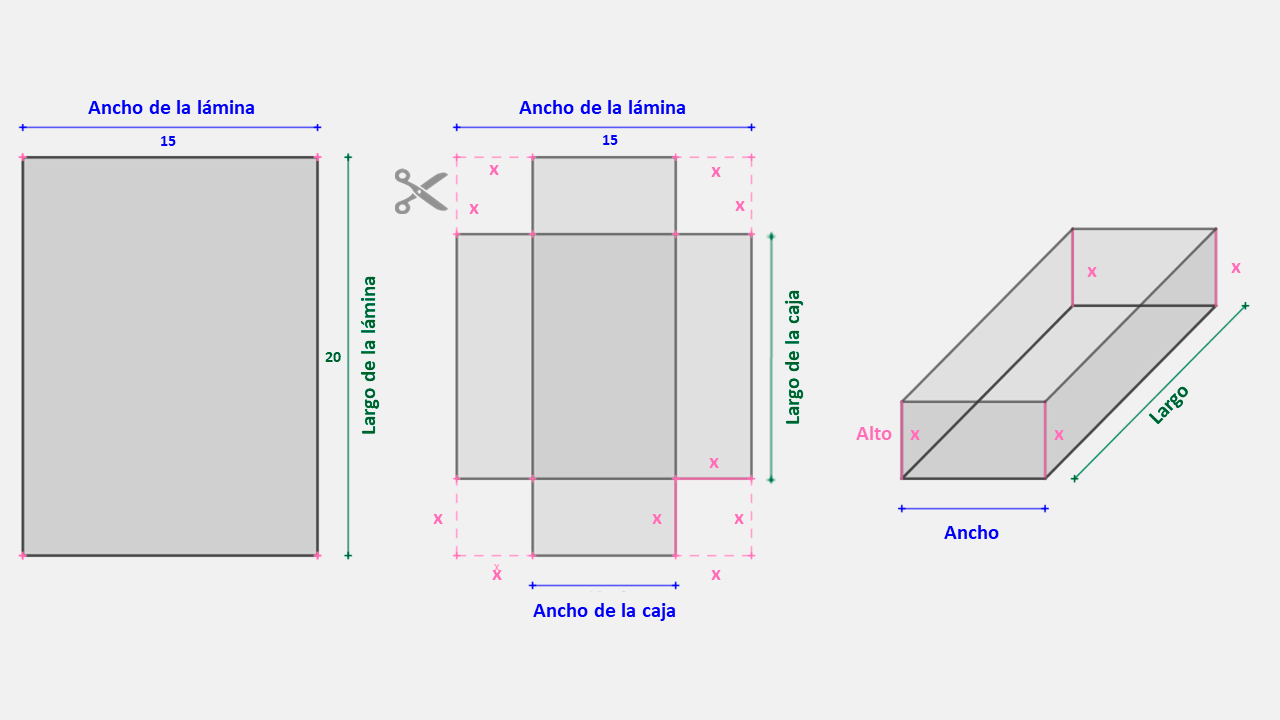
Se construye una caja sin tapa con una lámina rectangular de 20 centímetros de largo y 15 centímetros de ancho. Para construirla, se cortan cuadrados congruentes en las cuatro esquinas del cartón; luego se doblan las pestañas resultantes hacia arriba ¿Qué longitud deben tener los cortes para obtener una caja con el mayor volumen posible?
En la figura se muestra el modelo geométrico de la caja construida. Observa que la longitud del cuadrado x corresponde a la profundidad (altura) de la caja.
Para determinar el modelo algebraico que representa el volumen de la caja como una función de la profundidad debemos determinar las siguientes dimensiones: a) largo de la lámina; b) ancho de la lámina; c) profundidad o altura de la caja; d) largo de la caja; e) ancho de la caja ¿Puedes hacerlo? Completa los datos de la tabla.
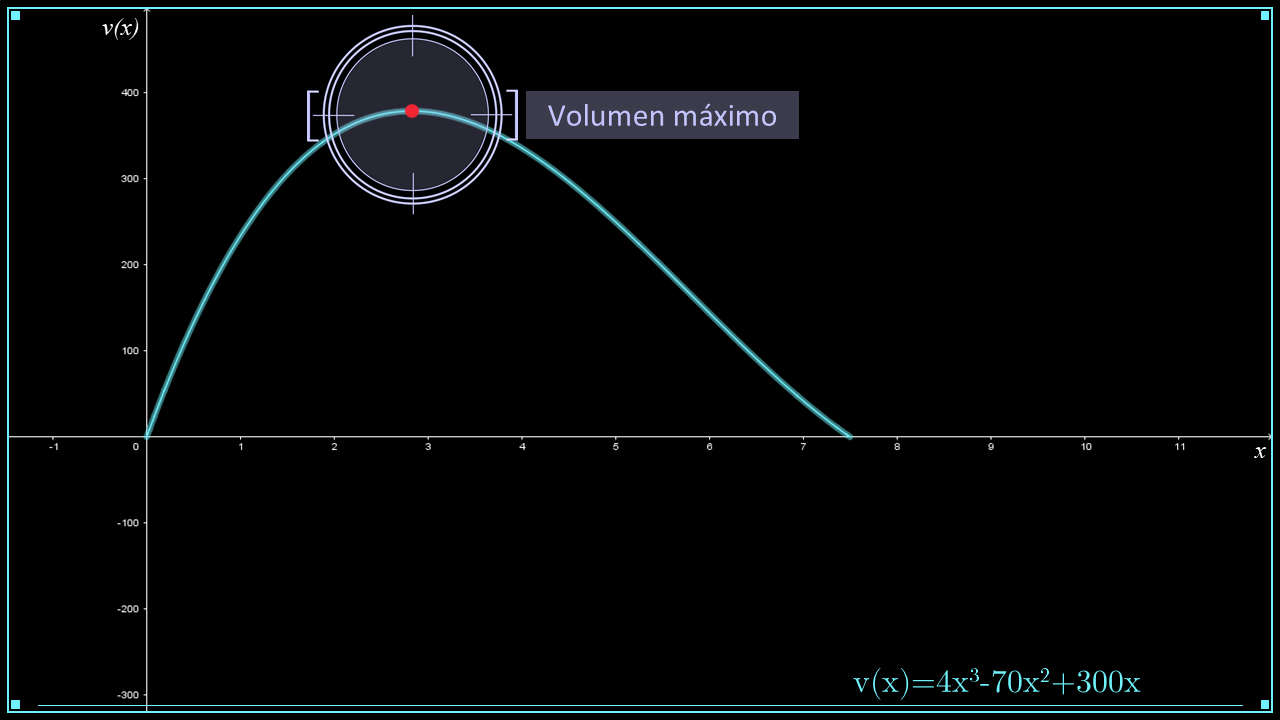
Ya que has determinado las expresiones algebraicas para las dimensiones de la caja, determina el modelo algebraico que representa el volumen como una función de la profundidad. Selecciona la opción correcta.
Considerando que las dimensiones de la caja no pueden ser negativas, las relaciones de orden para cada una de ellas son:
| Dimensión de la caja | Relación de orden |
|---|---|
| Profundidad o altura de la caja | $x \ge 0$ |
| Largo de la caja | $20 - 2x \ge 0$ |
| Ancho de la caja | $15 - 2x \ge 0$ |
A partir de las relaciones de orden, indica la condición para la profundidad de la caja:
El valor de la altura que implica un volumen máximo se encuentra entre $2$ y $3$. Para determinar el volumen máximo, se determina la primera derivada de $V\left( x \right) = 4{x^3} - 70{x^2} + 300x$.
Selecciona la opción que indica la derivada del volumen:
