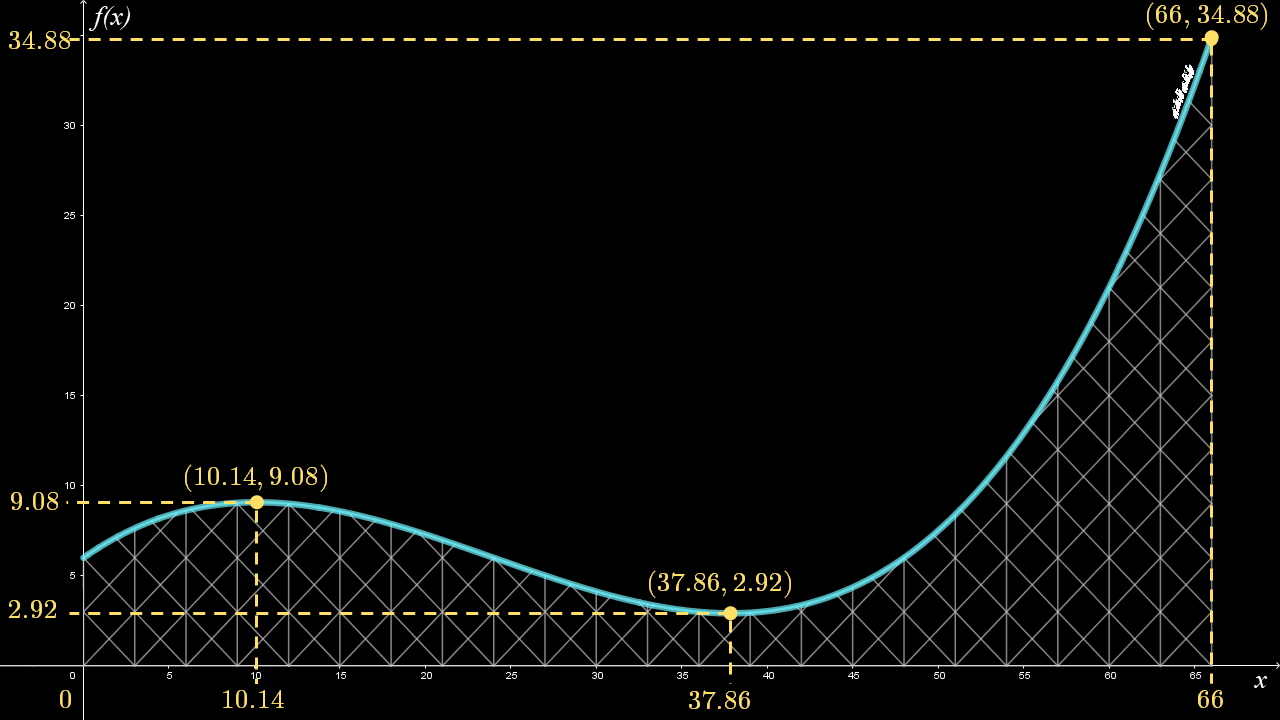
En la figura 1 se muestra el tramo de una montaña rusa. El modelo algebraico $f\left( x \right) = \frac{1}{{{{12}^3}}}{x^3} - \frac{6}{{{{12}^2}}}{x^2} + \frac{2}{3}x + 6$ describe la trayectoria de los carros, donde $x$ es la posición horizontal y $f$ es la altura como función de $x$. La variable independiente $x$ toma valores desde 0 hasta 66 (en metros); mientras que la altura tiene valores desde $2.92$ hasta $34.88$ (también en metros).
La gráfica de la función describe un comportamiento que se puede analizar con base en las siguientes definiciones:
Definición
Una función $f$ se llama:
• creciente sobre un intervalo $I$ si
$f\left( a \right) < f\left( b \right)$
siempre que $a < b$ en $I$
• decreciente sobre un intervalo $I$ si
$f\left( a \right) > f\left( b \right)$
siempre que $a < b$ en $I$
Definición
Sea $c$ un valor en el dominio de $f$. Decimos que $f\left( c \right)$ es:
• un valor máximo local de $f$ si $f\left( c \right) \ge f\left( x \right)$ cuando $x$ está cerca de $c$.
• un valor mínimo local de $f$ si $f\left( c \right) \le f\left( x \right)$ cuando $x$ está cerca de $c$.
• un valor máximo absoluto de $f$ si $f\left( c \right) \ge f\left( x \right)$ para toda $x$ en el dominio de la función.
• un valor mínimo absoluto de $f$ si $f\left( c \right) \le f\left( x \right)$ para toda $x$ en el dominio de la función.
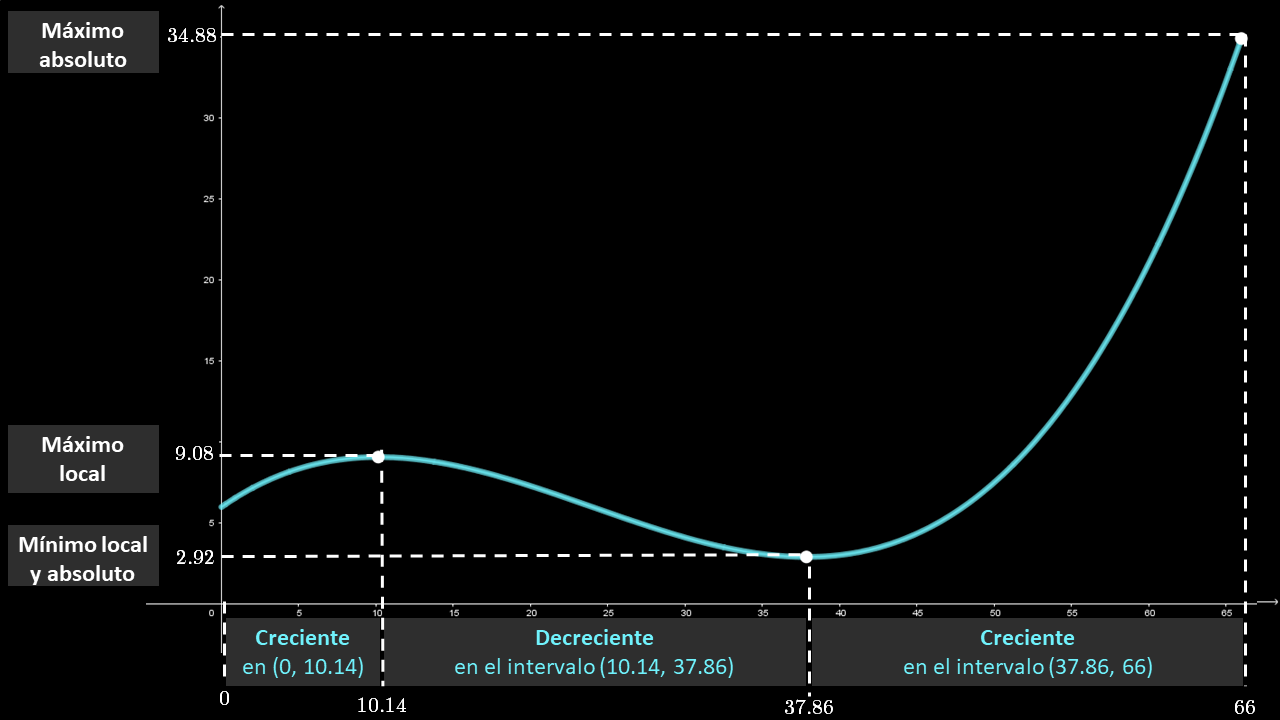
Por tanto, podemos afirmar que la gráfica de la función tiene las siguientes características:
• Es creciente en los intervalos $\left( {0,10.14} \right)$ y $\left( {37.86,66} \right)$.
• Es decreciente en el intervalo $\left( {10.14,37.86} \right)$.
• $f\left( {10.14} \right) = 9.08$ es un valor máximo local en $x=10.14$ y $f\left( {66} \right) = 34.88$ un valor máximo absoluto en $x=66$ (este máximo no es local porque se encuentra en un punto final).
• $f\left( {37.86} \right) = 2.92$ es un valor mínimo tanto local como absoluto en $x=37.86$.
Para describir el comportamiento de una función es necesario identificar los intervalos de crecimiento y decrecimiento, así como los valores donde la función presenta máximos y mínimos; en las siguientes secciones describirás estas características de una función a partir del análisis de sus rectas tangentes, así como de sus derivadas.
Valores máximo y mínimo locales y números críticos
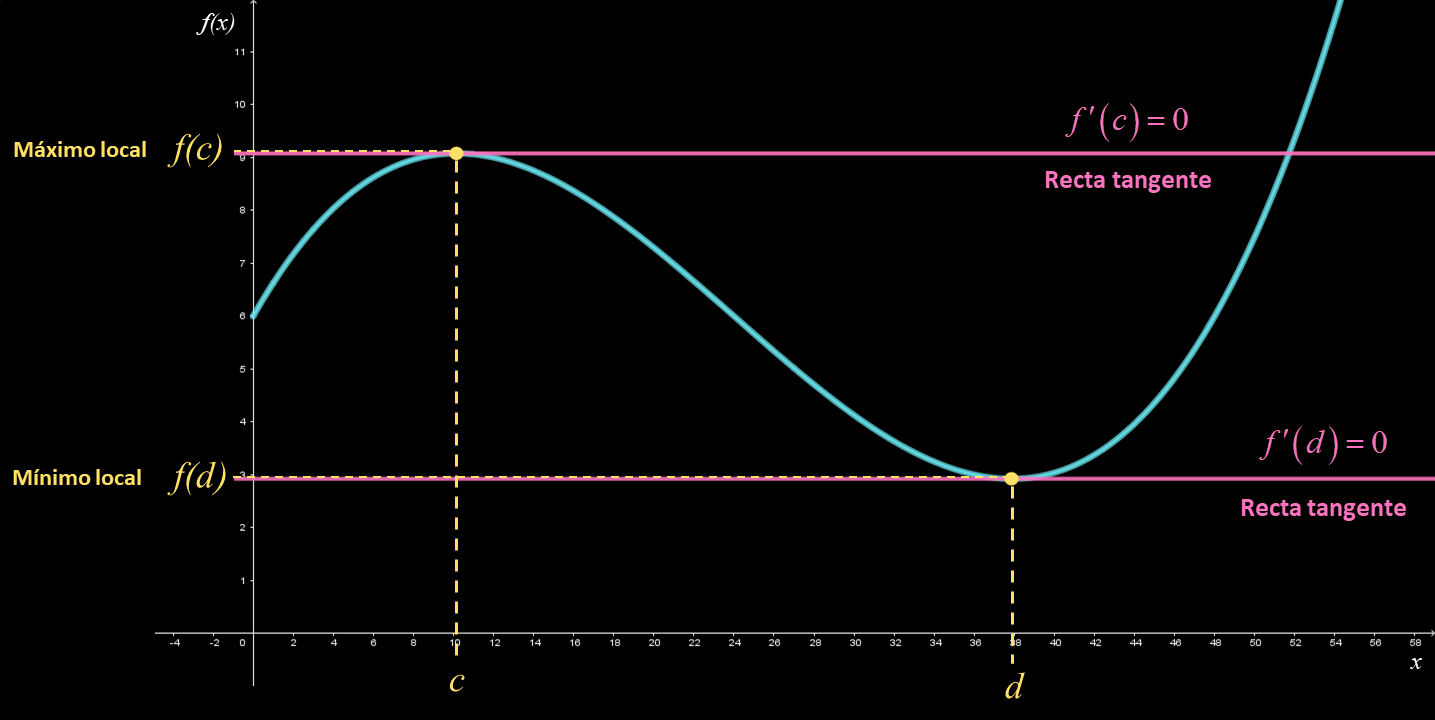
En los valores máximo y mínimo locales se tiene que la recta tangente es horizontal y, por tanto, la derivada es cero.
En los máximos y mínimos locales se tiene que la recta tangente es horizontal, cuya pendiente es $0$ ; por tanto, la derivada es $0$. De modo que si se tiene un máximo local en $x=c$, entonces $f'\left( c \right) = 0$; y si existe un mínimo local en $x=d$, entonces $f'\left( d \right) = 0$. En este sentido, el Teorema de Fermat establece lo siguiente:
Teorema de Fermat
Si $f$ tiene un máximo o mínimo local en $c$, y si $f'\left( c \right)$ existe, entonces $f'\left( c \right) = 0$.
Cabe mencionar que aun cuando $f'\left( c \right) = 0$, no implica que necesariamente hay un máximo o mínimo en $c$. Por lo que no es correcto aplicar el Teorema de Fermat de forma inversa. En el apartado Para saber más se ejemplificará esta situación.
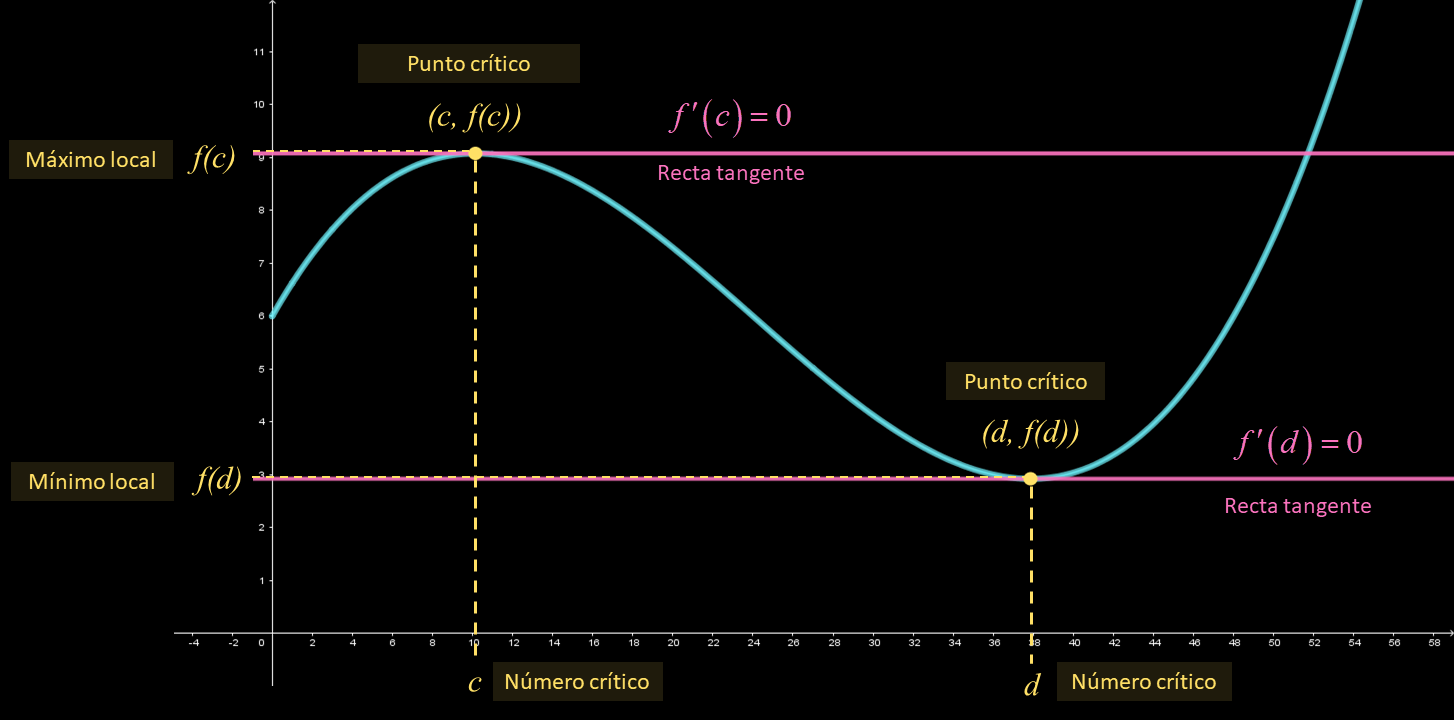
Al valor $c$ donde se presenta el máximo o mínimo local se le conoce como número crítico de $f$. Cabe mencionar que existen números críticos donde la derivada no existe; por ejemplo, cuando la gráfica tiene una asíntota vertical o un salto.
Número crítico
Un número crítico de una función $f$ es un número $c$ en el dominio de $f$ tal que $f'\left( c \right) = 0$ o $f'\left( c \right) $ no existe. Al punto $\left( {c,f\left( c \right)} \right)$ se le denomina punto crítico.
En la siguiente figura se ilustran números y puntos críticos.
En los siguientes ejemplos se muestra que en los valores máximos o mínimos locales se tiene que el valor de la derivada es cero, tal como establece el Teorema de Fermat.
-
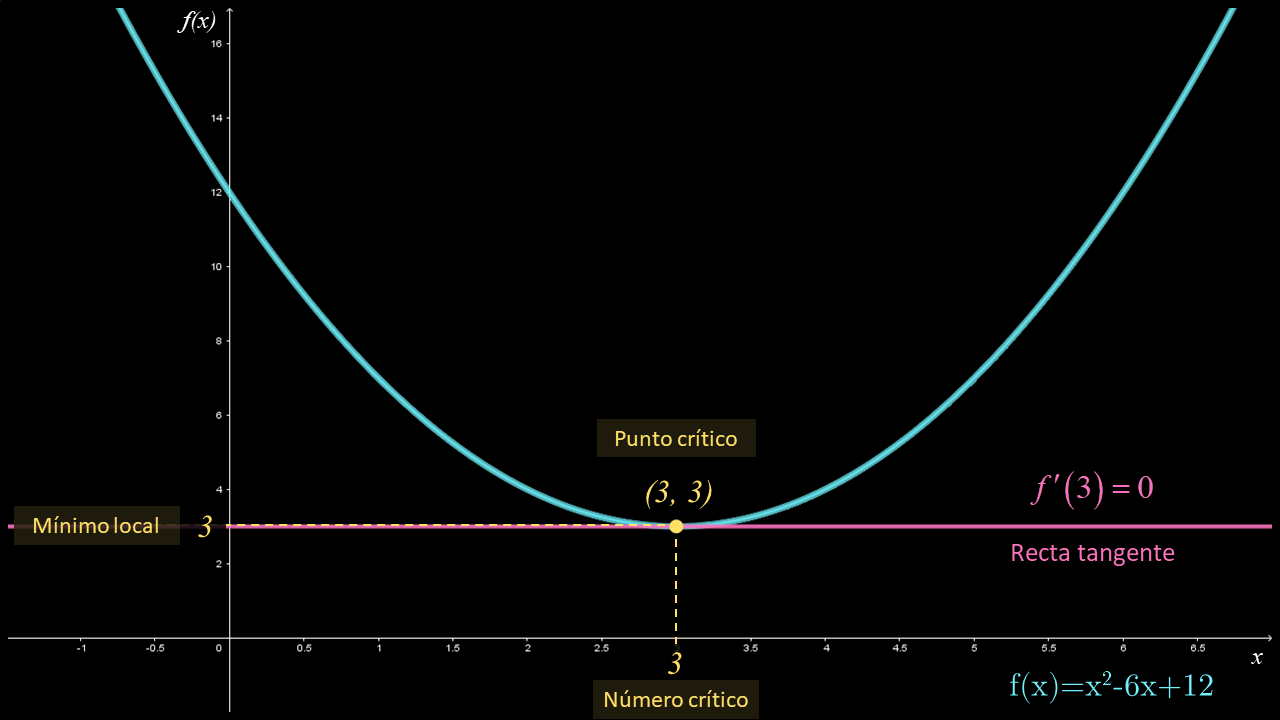
Ejemplo 1
Dada la función $f\left( x \right) = {x^2} - 6x + 12$, con un valor mínimo local en el número crítico $x=3$ y derivable en dicho número. Determina el valor de la derivada en el punto crítico.
Solución
Con base en el Teorema de Fermat se concluye que $f'\left( 3 \right) = 0$ en el número crítico $x=3$; por tanto, la recta tangente es horizontal en el punto crítico $\left( {3,f\left( 3 \right)} \right) = \left( {3,3} \right)$. Para comprobar esta afirmación se determina la derivada de $f$ y se evalúa en $x=3$:
$\begin{array}{l} f'\left( x \right) = 2x - 6\\ f'\left( 3 \right) = 2\left( 3 \right) - 6 = 0 \end{array}$
La expresión anterior demuestra que, en el punto crítico la derivada es cero. Asimismo, la gráfica muestra que se tiene un mínimo local en $x=3$; en consecuencia, $f'\left( 3 \right) = 0$.
-
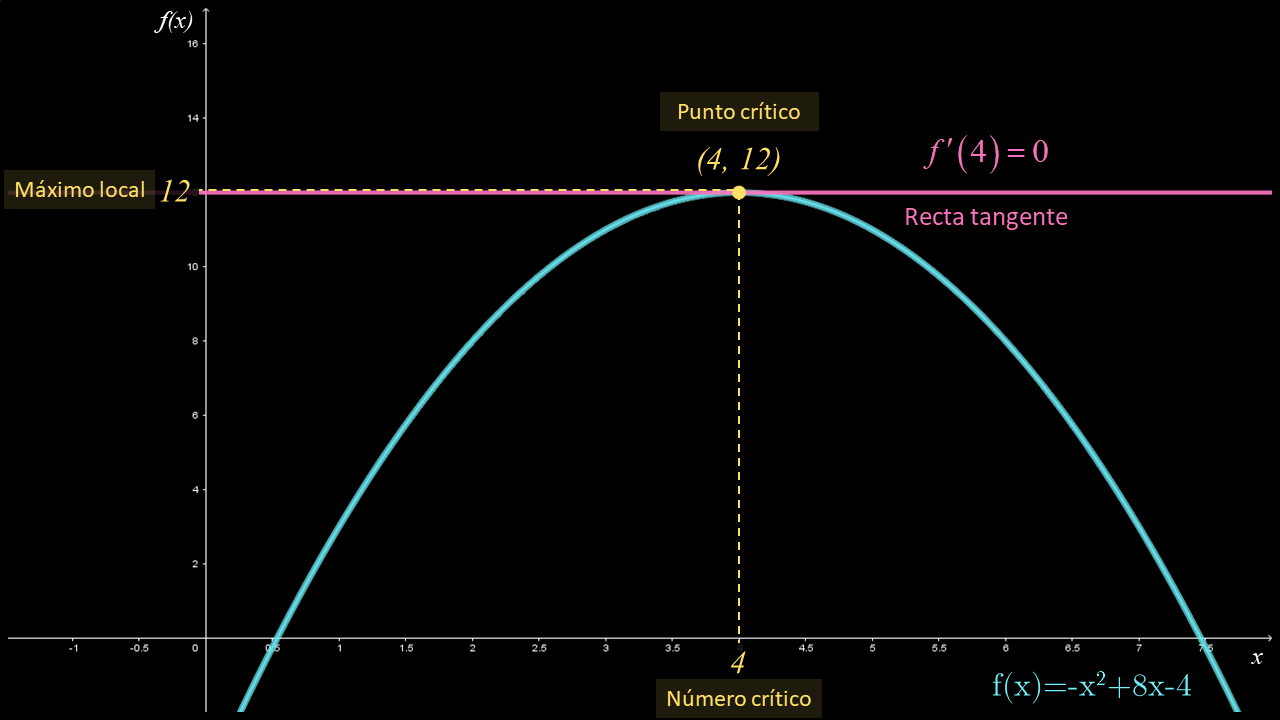
Ejemplo 2
Dada la función $f\left( x \right) = - {x^2} + 8x - 4$, con un valor máximo local en el número crítico X=4 y derivable en dicho número. Determina el valor de la derivada en el punto crítico.
Solución
Por el Teorema de Fermat se tiene que $f'\left( 4 \right) = 0$ en el número crítico $x=4$; por tanto, la recta tangente es horizontal en el punto crítico $\left( {4,f\left( 4 \right)} \right) = \left( {4,12} \right)$. Para comprobar esta afirmación se determina la derivada de $f$ y evaluamos en $x=4$:
$\begin{array}{l} f'\left( x \right) = - 2x + 8\\ f'\left( 4 \right) = - 2\left( 4 \right) + 8 = 0 \end{array}$
La expresión anterior demuestra que, en el punto crítico la derivada es cero. Asimismo, la gráfica muestra que se tiene un máximo local en $x=4$; en consecuencia, $f'\left( 4 \right) = 0$.
-
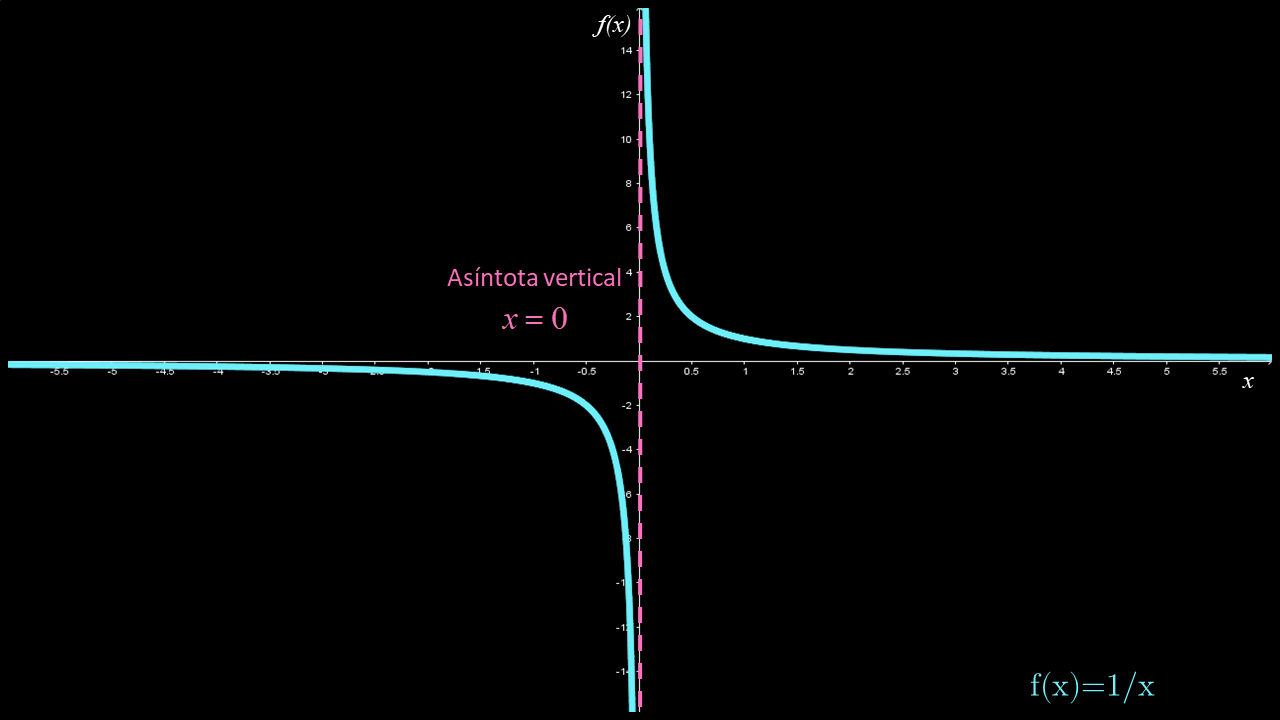
Ejemplo 3
Dada la función $f\left( x \right) = \frac{1}{x}$, determina, si existen, sus números críticos, así como el valor de la derivada en dichos números.
Solución
Por definición, el número crítico $x=c$ se presenta donde $f'\left( c \right) = 0$ o donde $f'\left( c \right)$ no existe. Por tanto, al obtener la derivada de la función se tiene que
$f'\left( x \right) = - \frac{1}{{{x^2}}}$
De la expresión anterior se observa que $f'$ no existe en $x=0$, ya que la división por cero no está definida. En consecuencia, la función tiene un número crítico en $x=0$.
La gráfica muestra que se tiene una asíntota vertical en el número crítico.
-
Para saber más
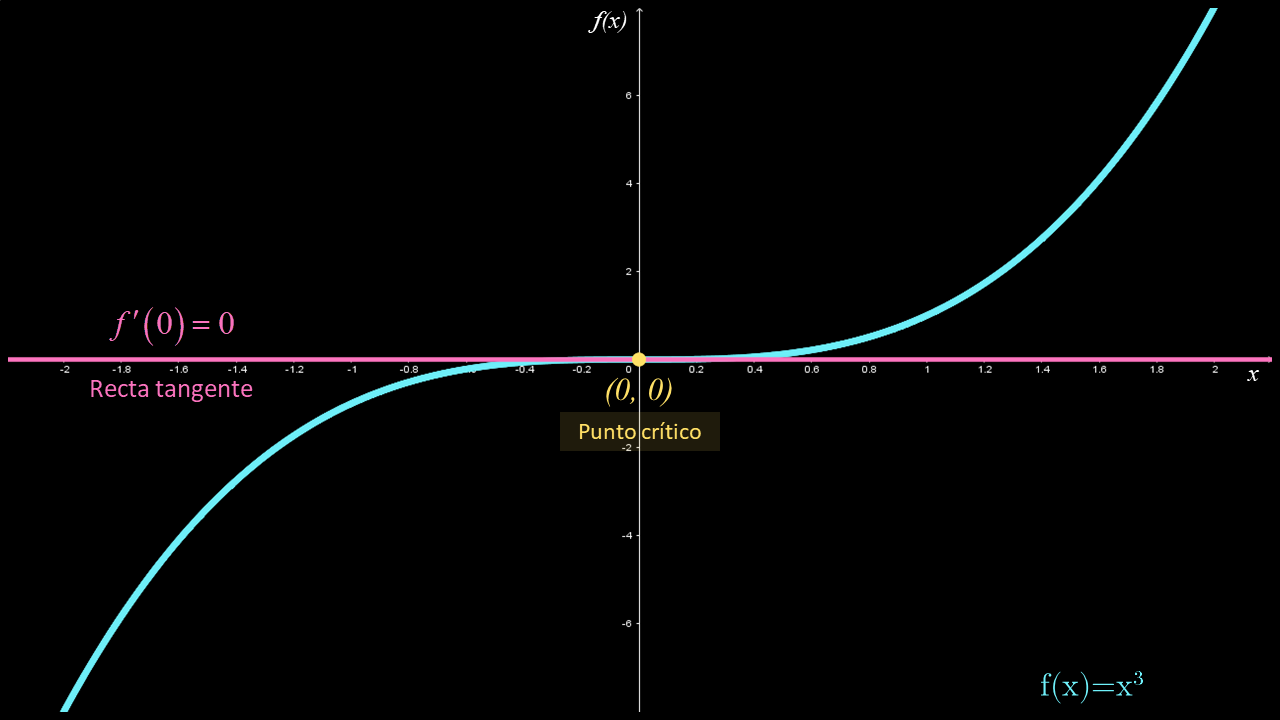
Cuando $f'\left( c \right) = 0$, no implica que necesariamente hay un máximo o mínimo en $c$. Por lo que no es correcto aplicar de forma inversa el Teorema de Fermat. Para ilustrar esta situación, considera la función $f\left( x \right) = {x^3}$ cuya derivada es $f'\left( x \right) = 3{x^2}$.
Después se encuentran los números críticos igualando la derivada a cero, es decir, $f'\left( x \right) = 0$:
$f'\left( x \right) = 3{x^2} = 0$
La igualdad anterior se cumple en el número crítico $x=0$. En consecuencia, se tiene un punto crítico en $\left( {0,0} \right)$ que, como se observa en la figura, no corresponde ni a un máximo ni a un mínimo (a este punto se le conoce como punto de inflexión, concepto que revisarás en las siguientes secciones). Por tanto, si se tiene que la derivada es cero en un punto crítico, no implica la existencia de un máximo o un mínimo, con lo que comprobamos que el Teorema de Fermat no se puede aplicar de forma inversa.
Si la derivada es cero en un punto crítico, no implica la existencia de un máximo o un mínimo.
En el siguiente ejercicio determinarás la derivada de una función en sus puntos críticos mediante el Teorema de Fermat para comprender los conceptos involucrados.
Dada la función $f\left( x \right) = - 2{x^3} + 6x - 1$, con un valor mínimo local en el número crítico $x=-1$ y un valor máximo local en el número crítico $x=1$; y derivable en todo su dominio. Determina la derivada de la función en los valores críticos considerando el teorema de Fermat; escribe tus resultados en los siguientes cuadros.