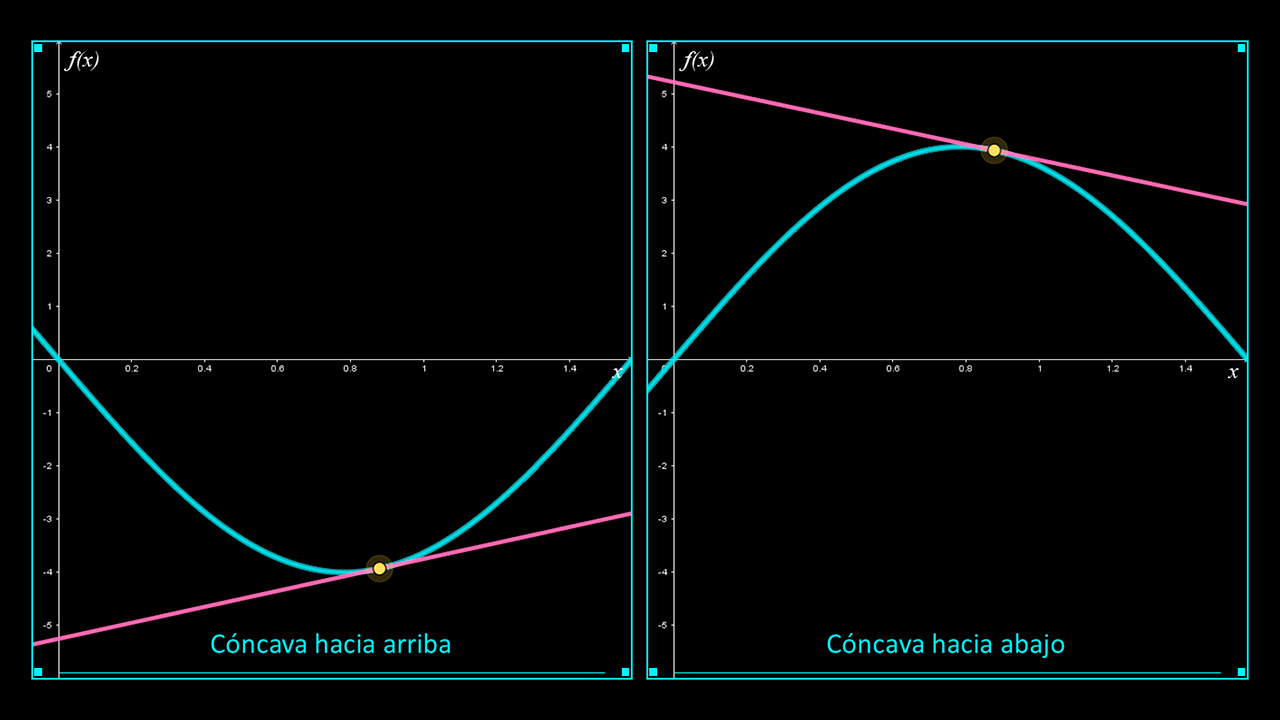
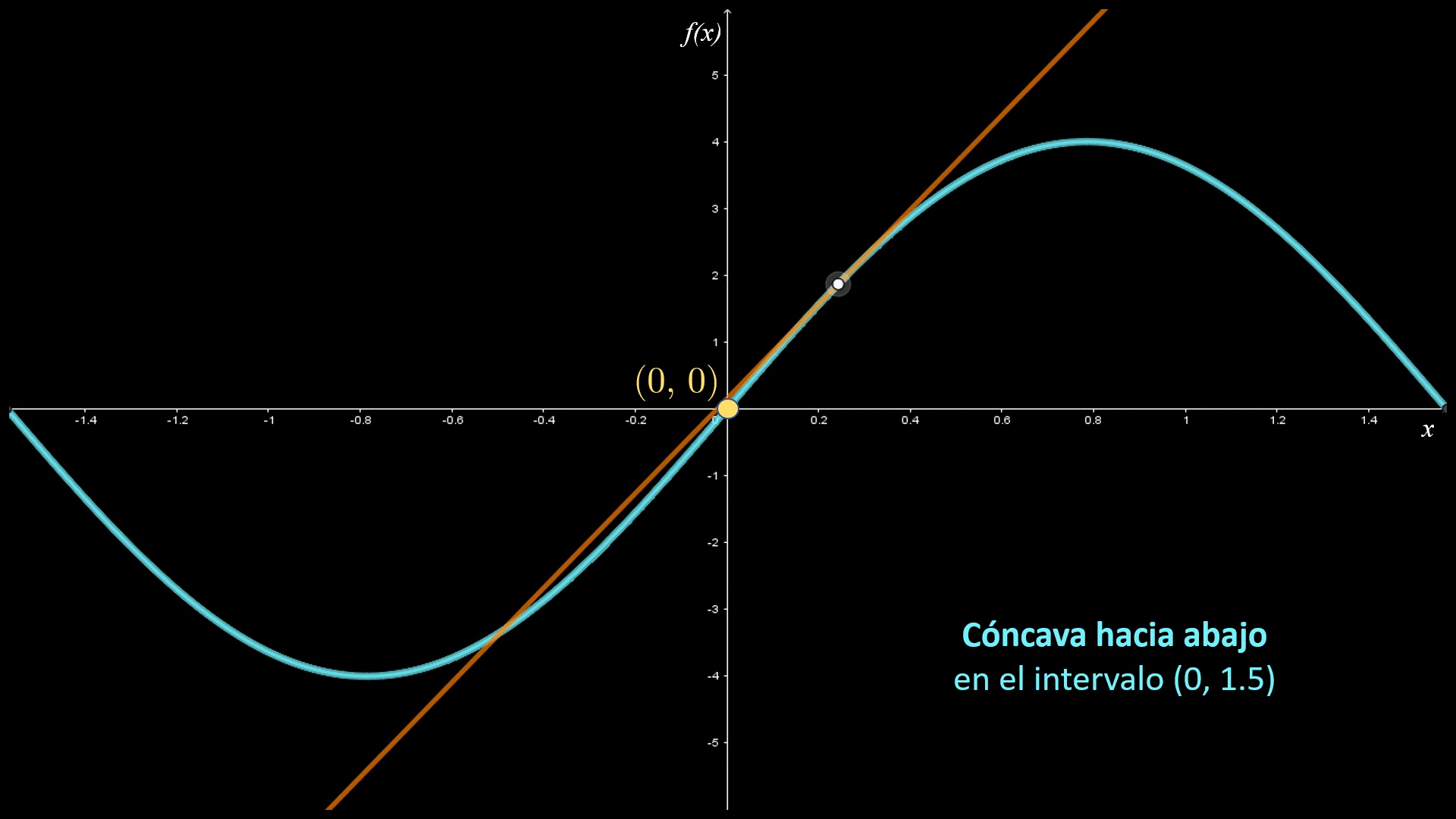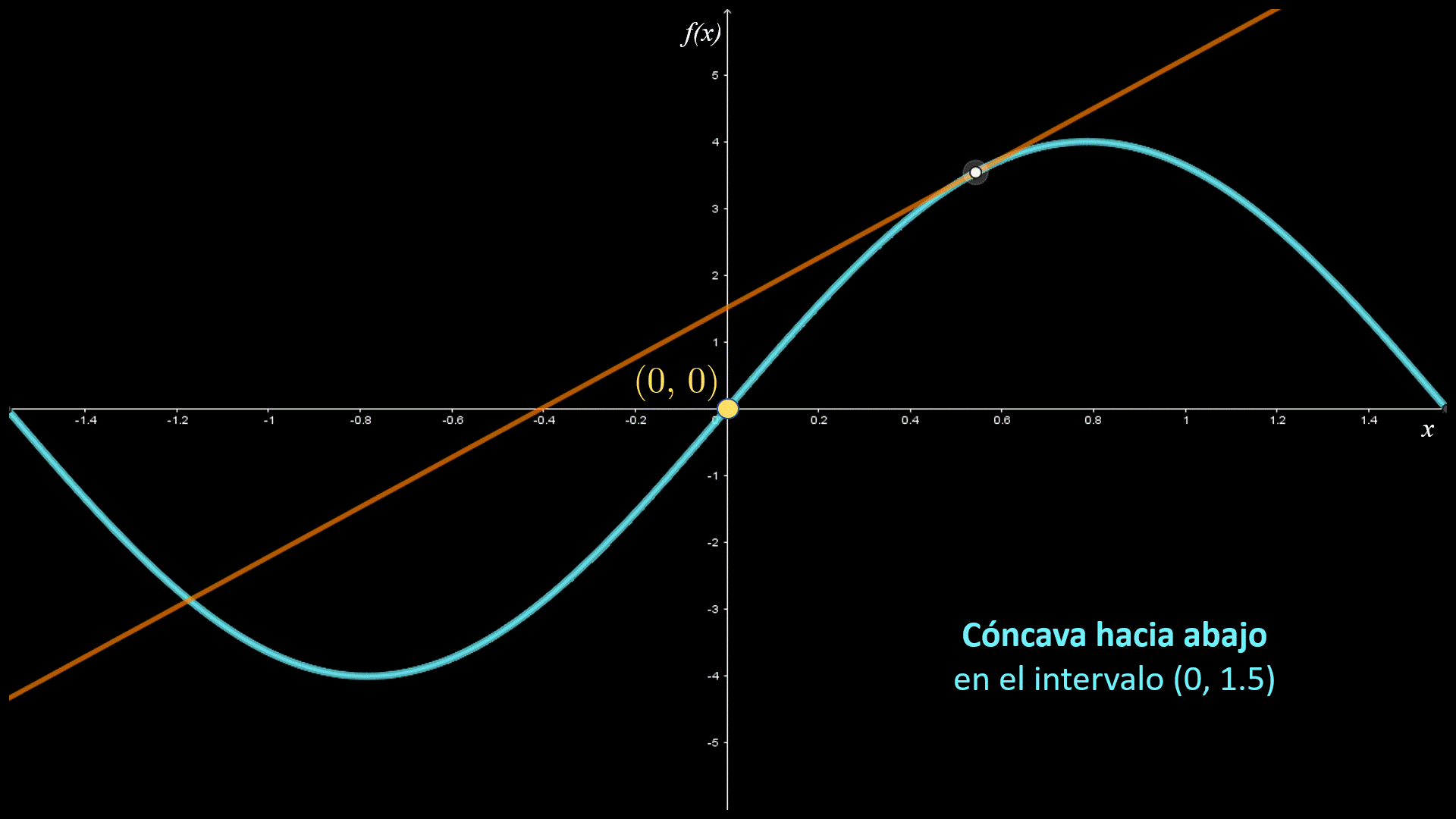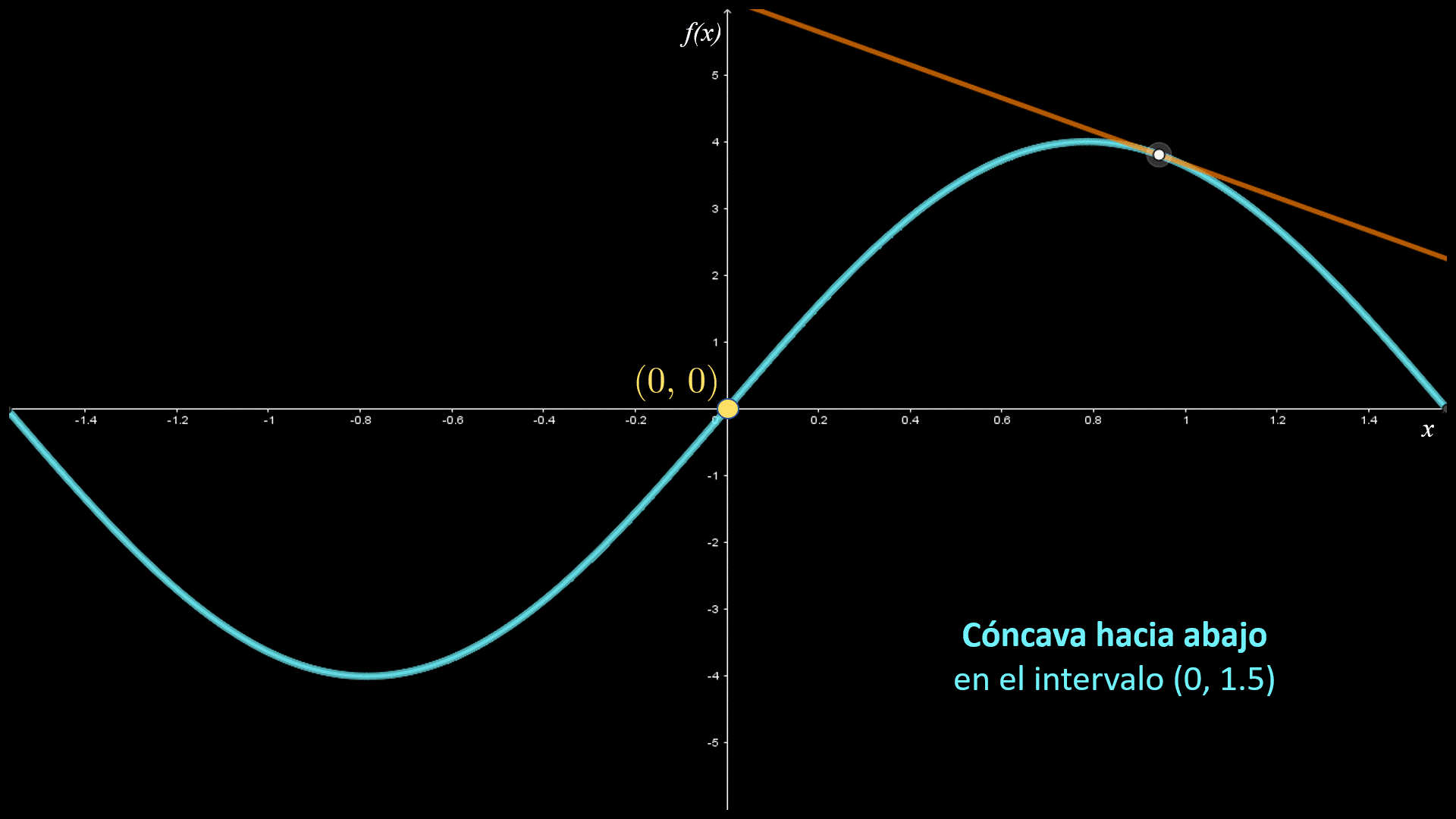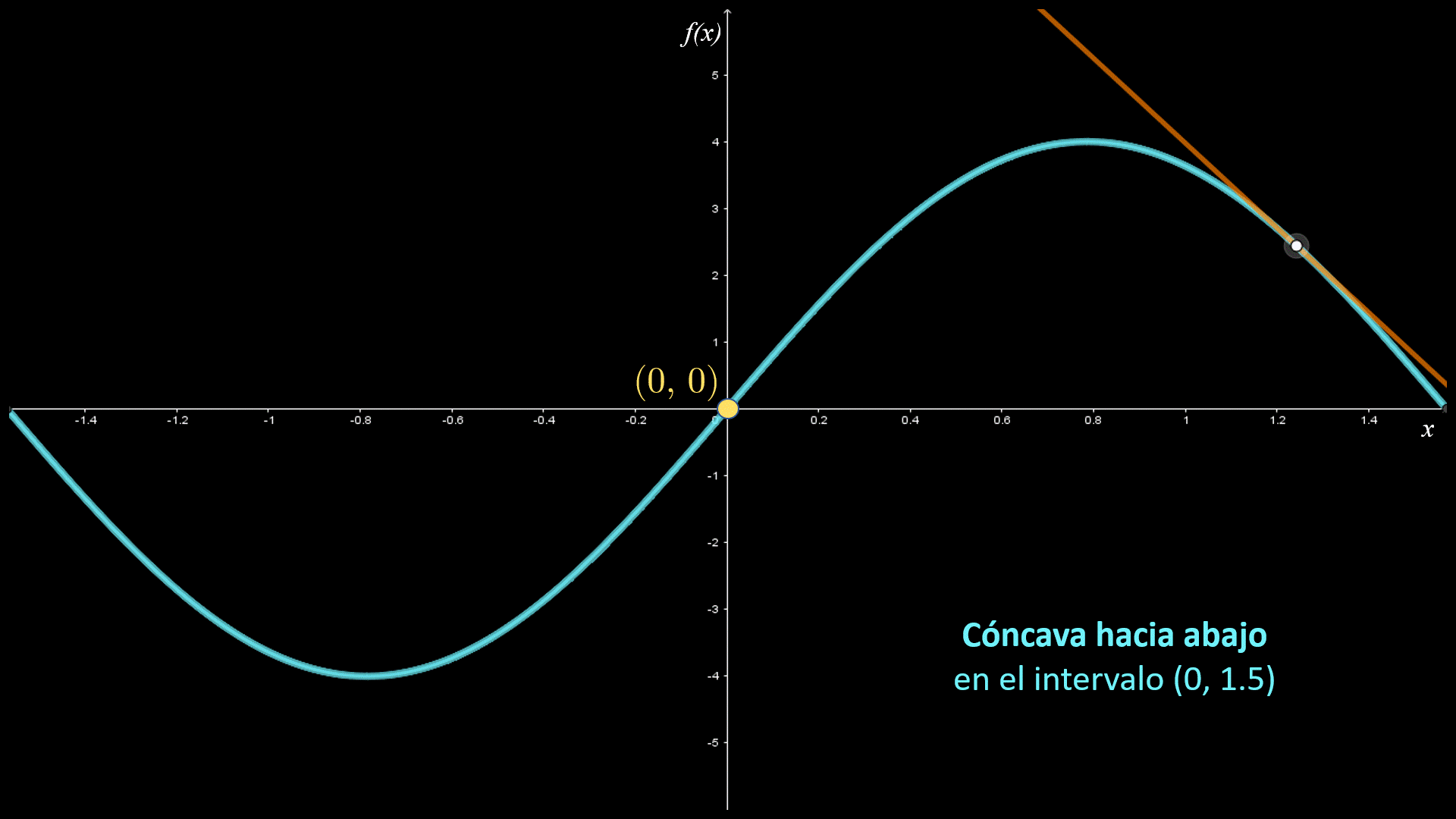
En las imágenes siguientes se muestran las gráficas de dos funciones con diferente concavidad: la primera es cóncava hacia arriba en el intervalo I1; y la segunda cóncava hacia abajo en el intervalo I2.
La primera gráfica es cóncava hacia arriba y la segunda es cóncava hacia abajo. La concavidad de una curva se puede definir a partir de la posición de la curva respecto a sus rectas tangentes.
Definición
Si la gráfica de una función está por arriba de todas sus rectas tangentes en un intervalo I, entonces se dice que es cóncava hacia arriba en dicho intervalo. Si la gráfica de una función está por abajo de todas sus rectas tangentes en un intervalo I, entonces se dice que es cóncava hacia bajo en dicho intervalo.
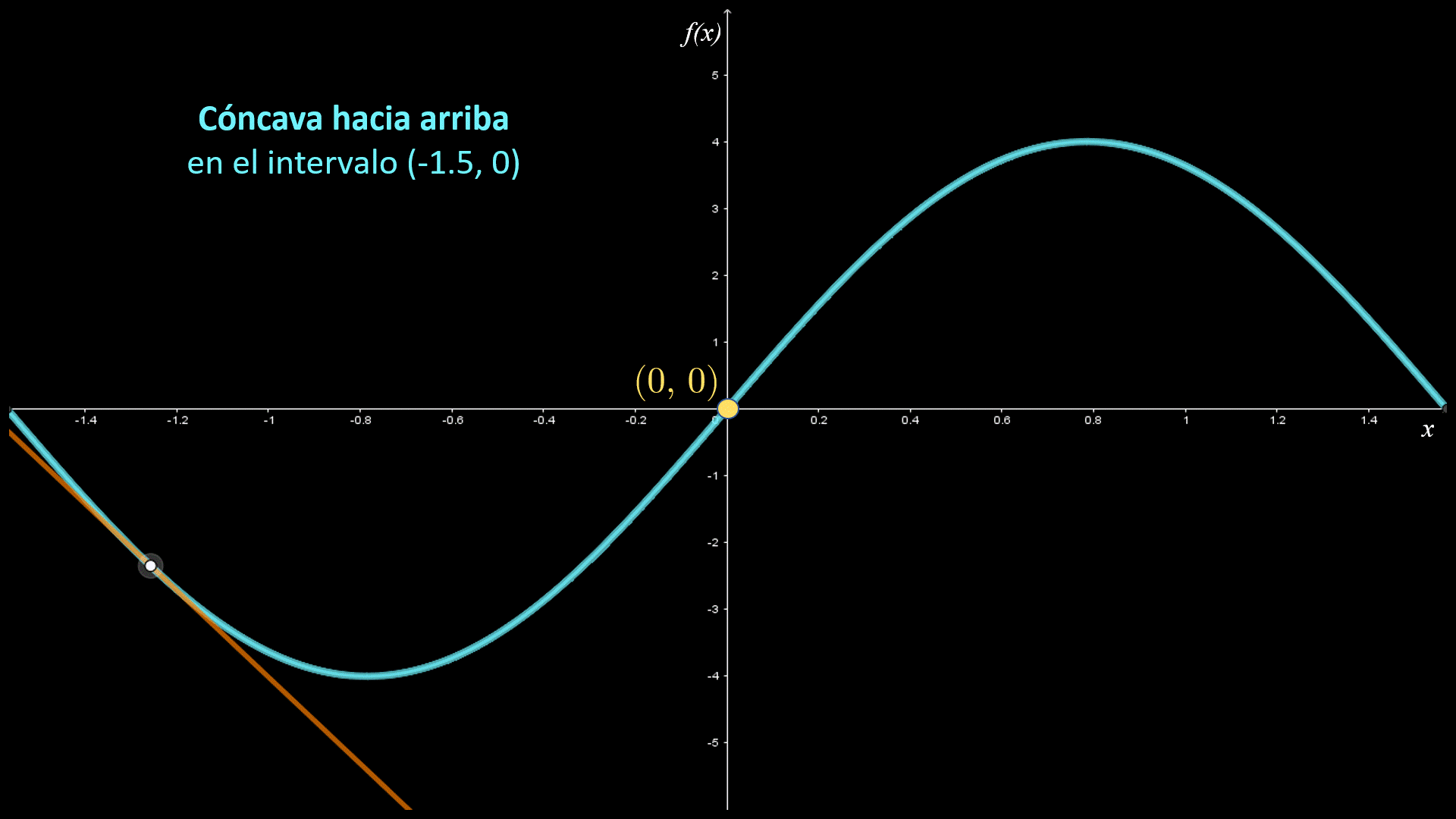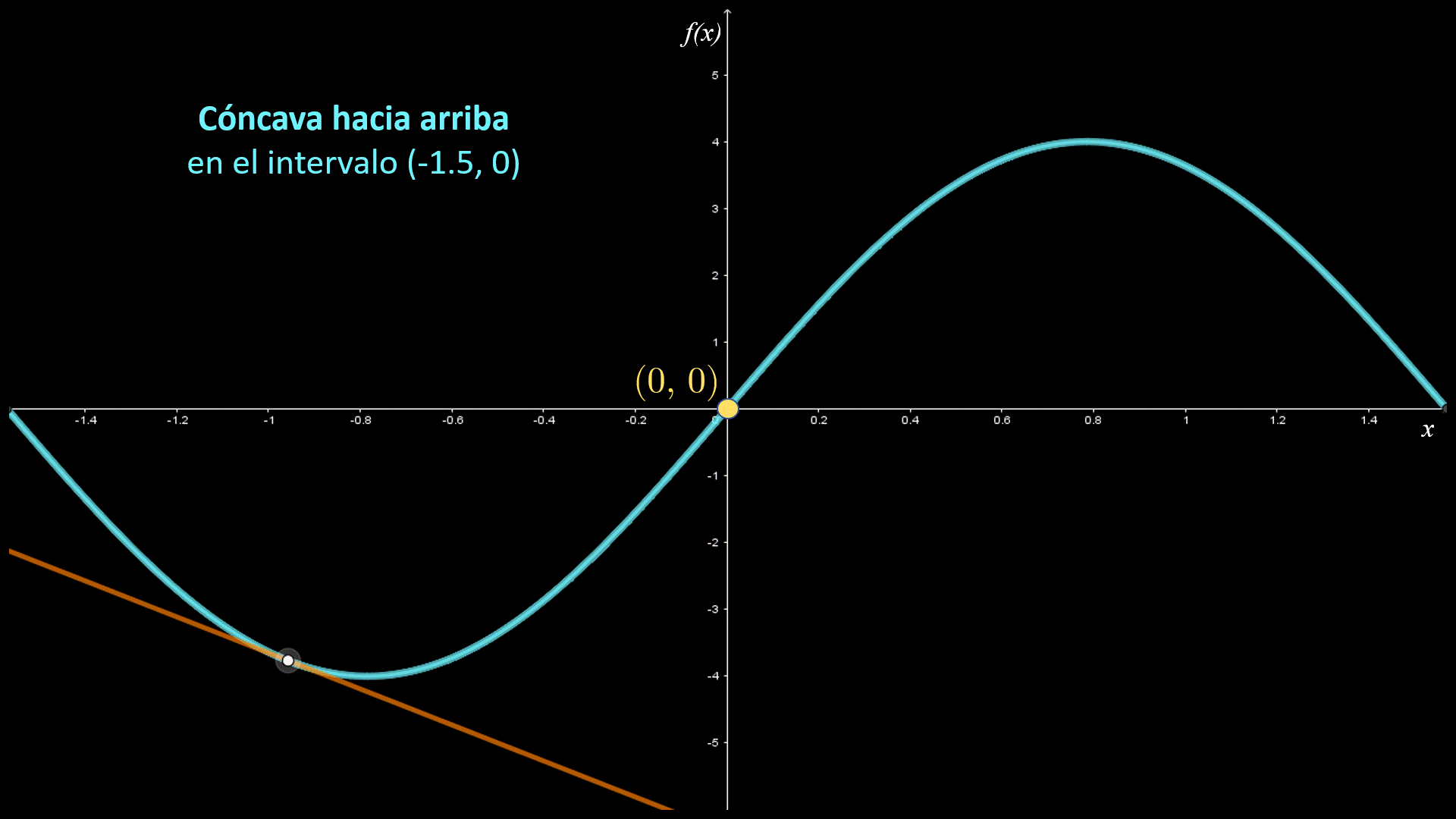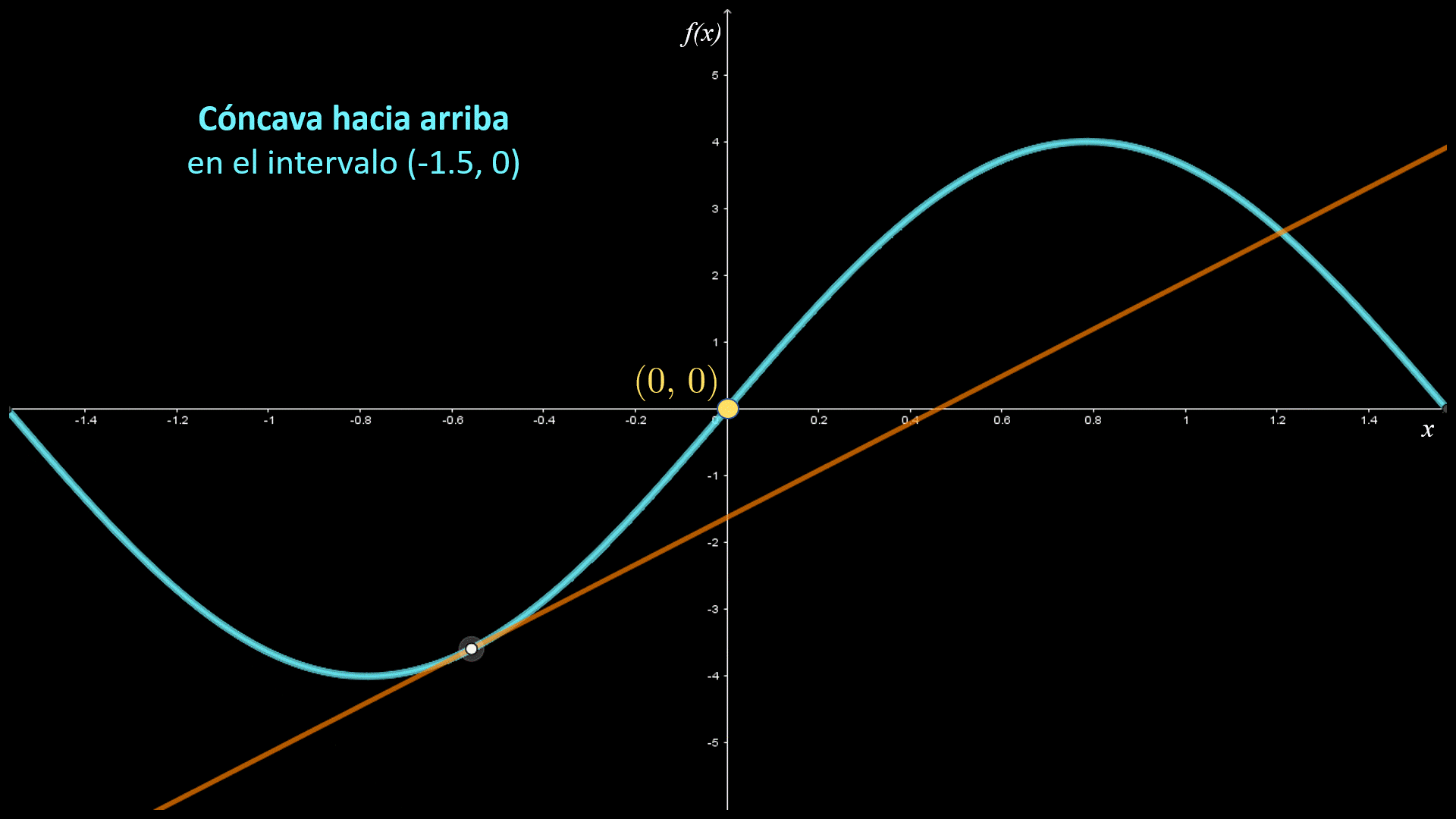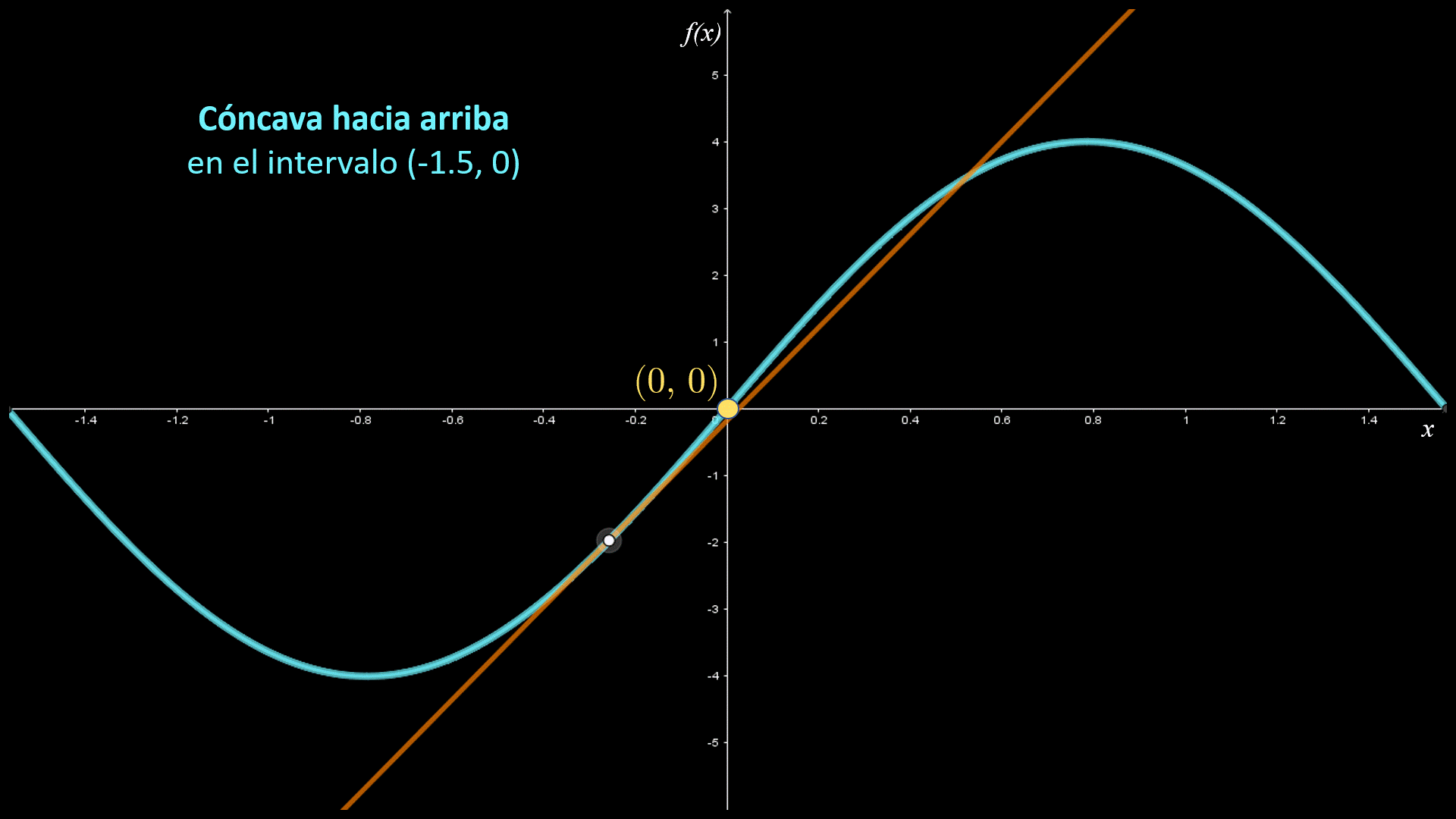
En las siguientes figuras se indican los intervalos de concavidad para la función $f\left( x \right)$. Observa que la gráfica es cóncava hacia arriba en el intervalo $\left( { - 1.5,0} \right)$, donde la gráfica está por arriba de sus rectas tangentes; asimismo, es cóncava hacía abajo en el intervalo $\left( {0,1.5} \right)$, donde la gráfica está por debajo de sus rectas tangentes.
La segunda derivada también ayuda a determinar los intervalos de concavidad, según se indica en el siguiente teorema:
Teorema de concavidad
Sea $f$ una función dos veces derivable sobre un intervalo abierto $\left( {a,b} \right)$
a) Si $f''\left( x \right) > 0$ para toda $x$ en el intervalo $\left( {a,b} \right)$, entonces la gráfica de $f$ es cóncava hacia arriba sobre el intervalo.
b) Si $f''\left( x \right) < 0$ para toda $x$ en el intervalo $\left( {a,b} \right)$, entonces la gráfica de $f$ es cóncava hacia arriba sobre el intervalo.
Cabe mencionar que todo teorema requiere una demostración; sin embargo, la demostración no se desarrollará en este material didáctico.
-
Ejemplo 1
Determina los intervalos de concavidad de las siguientes funciones utilizando la segunda derivada.
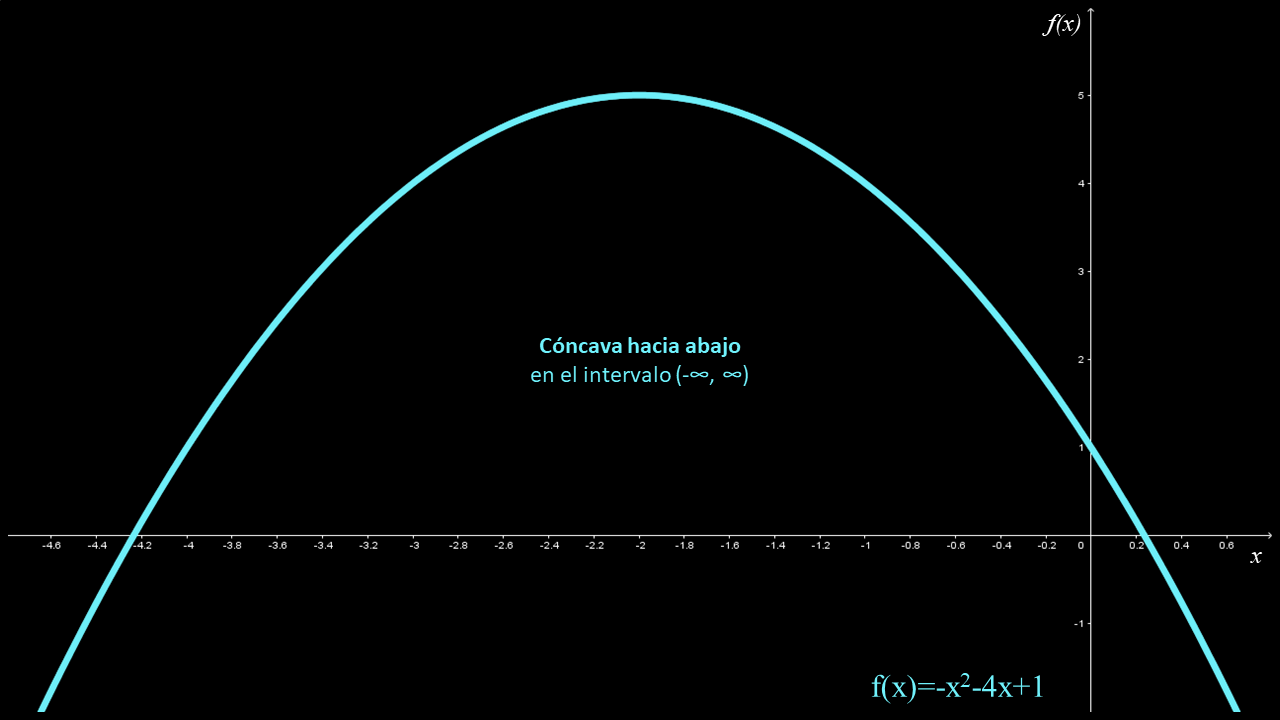
$f\left( x \right) = - {x^2} - 4x + 1$
Primero se determinan la primera y segunda derivadas de $f$:
$\begin{array}{l} f'\left( x \right) = - 2x - 4 = - 2\left( {x + 2} \right)\\ f''\left( x \right) = - 2 \end{array}$
La segunda derivada de $f$ es negativa en todo el dominio de la función, es decir:
$f''\left( x \right) = - 2 < 0$ para toda $x$ sobre el intervalo $\left( { - \infty ,\infty } \right)$
Por el Teorema de concavidad podemos afirmar que la gráfica de $f$ es es cóncava hacia abajo sobre el intervalo $\left( { - \infty ,\infty } \right)$, tal como se muestra en la siguiente figura.
-
Ejemplo 2
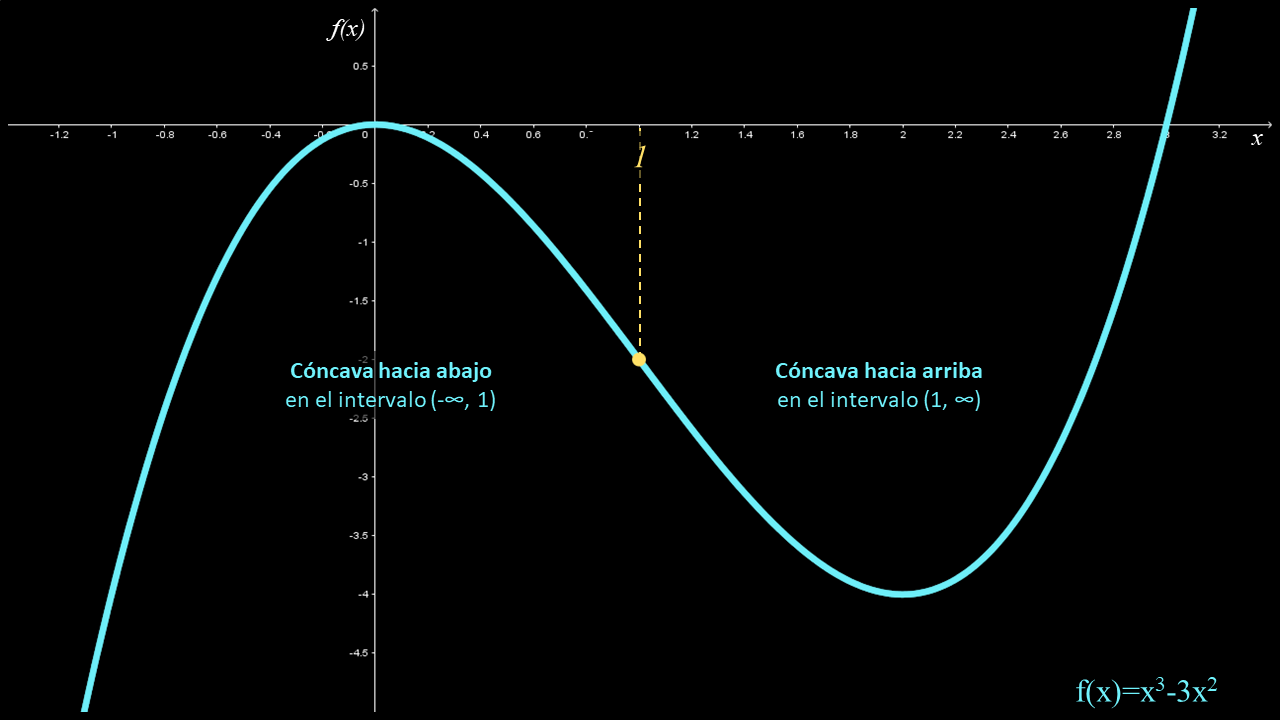
$y = {x^3} - 3{x^2}$
Primero se determinan la primera y segunda derivadas de $f$:
$\begin{array}{l} f'\left( x \right) = 3{x^2} - 6x = 3x\left( {x - 2} \right)\\ f''\left( x \right) = 6x - 6 = 6\left( {x - 1} \right) \end{array}$
Para aplicar el teorema de concavidad se resuelven dos desigualdades:
Desigualdades Intervalo donde se cumple la desigualdad Concavidad de $f$ $f''\left( x \right) = 6\left( {x - 1} \right) < 0$ $\left( { - \infty ,1} \right)$
Se cumple la desigualdad en cualquier valor en este intervalo. Por ejemplo, si $x = 0$ entonces $f''\left( 0 \right) = - 6< 0$Cóncava hacia abajo $f''\left( x \right) = 6\left( {x - 1} \right) > 0$ $\left( {1,\infty } \right)$
Se cumple la desigualdad en cualquier valor en este intervalo. Por ejemplo, si $x = 3$ entonces $f''\left( 3 \right) = 12 > 0$Cóncava hacia arriba Con base en tabla anterior, podemos afirmar que la gráfica de $f$ es cóncava hacia abajo sobre el intervalo $\left( { - \infty ,1} \right)$ y cóncava hacia arriba en el intervalo $\left( {1,\infty } \right)$, tal como se muestra en la siguiente figura.
El desarrollo de los ejercicios te permitirá determinar, a través del análisis gráfico y algebraico, el tipo de concavidad de la función a partir del signo de la segunda derivada.
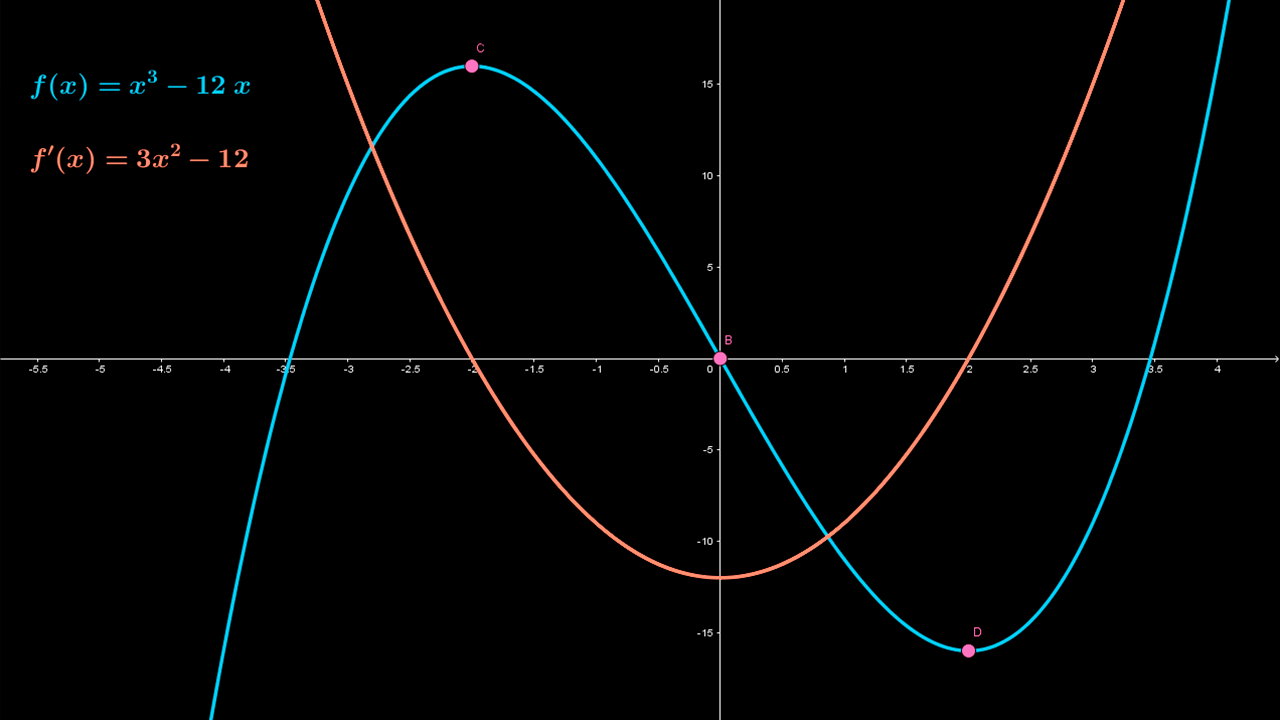
Analiza la gráfica de la función $f\left( x \right) = {x^3} - 12x$, así como la gráfica de la función derivada $f'\left( x \right) = 3{x^2} - 12$, y selecciona la opción correcta; revisa el recurso GeoGebrapara realizar tu análisis.
Selecciona en los intervalos especificados en la tabla, si la derivada de la función $f'(x)=3x^2-12$ es creciente o decreciente.
Dada la función $f\left( x \right) = - 2{x^3} + 3{x^2}$, responde las siguientes preguntas de opción múltiple.
1. La derivada de la función $f$ es:
2. La segunda derivada de la función $f$ es:
3. Para aplicar el Teorema de concavidad, se divide el dominio de $f$ en los intervalos:
4. La gráfica de la función es cóncava hacia a arriba en el intervalo:
5. La gráfica de la función es cóncava hacia abajo en el intervalo: