En las secciones anteriores observaste que un número crítico da lugar a diferentes tipos de puntos críticos (máximos y mínimos locales y puntos de inflexión). En esta sección y la siguiente utilizarás los llamados criterios de la primera y segunda derivada para identificar a los diferentes tipos de puntos críticos.
Criterio de la 1ª derivada
Sea $c$ un número crítico de una función continua $f$.
a) Si $f'$ cambia de positiva a negativa en $c$, entonces $f$ tiene un máximo local en $c$.
b) Si $f'$ cambia de negativa a positiva en $c$, entonces $f$ tiene un mínimo local en $c$.
c) Si $f'$ no cambia de signo en $c$, entonces $f$ no tiene ningún máximo o mínimo local en $c$.
-
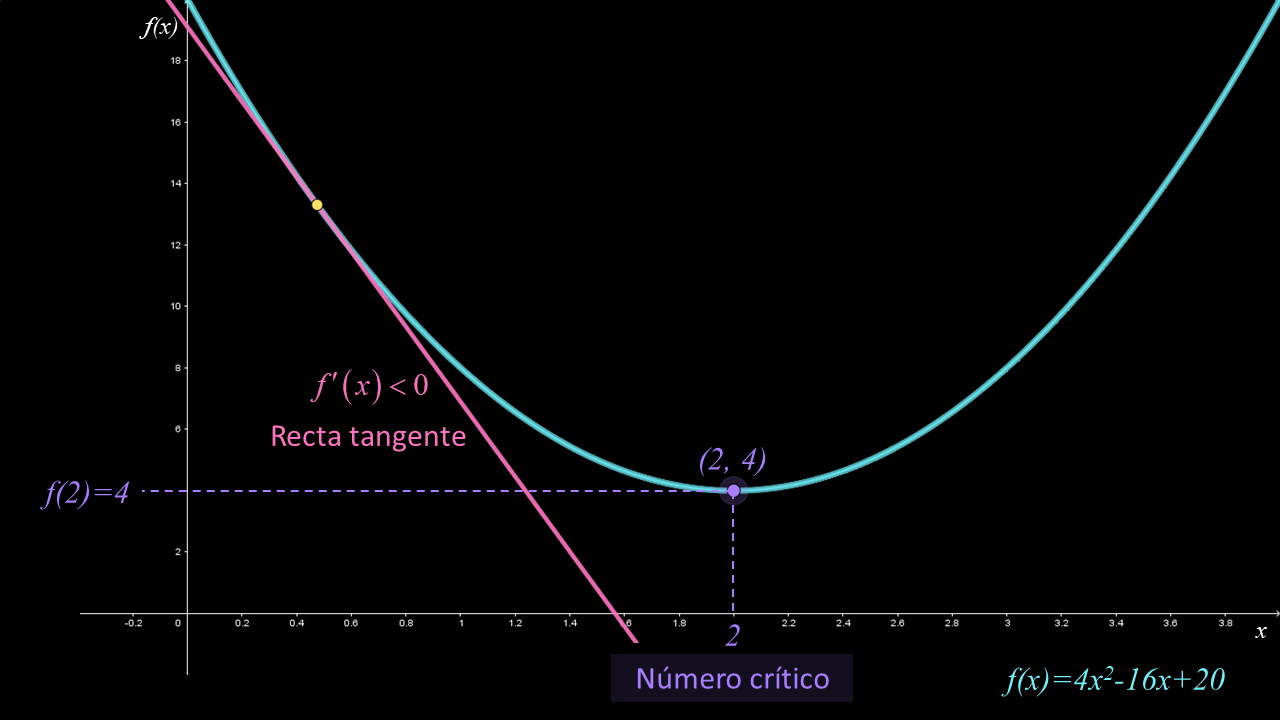
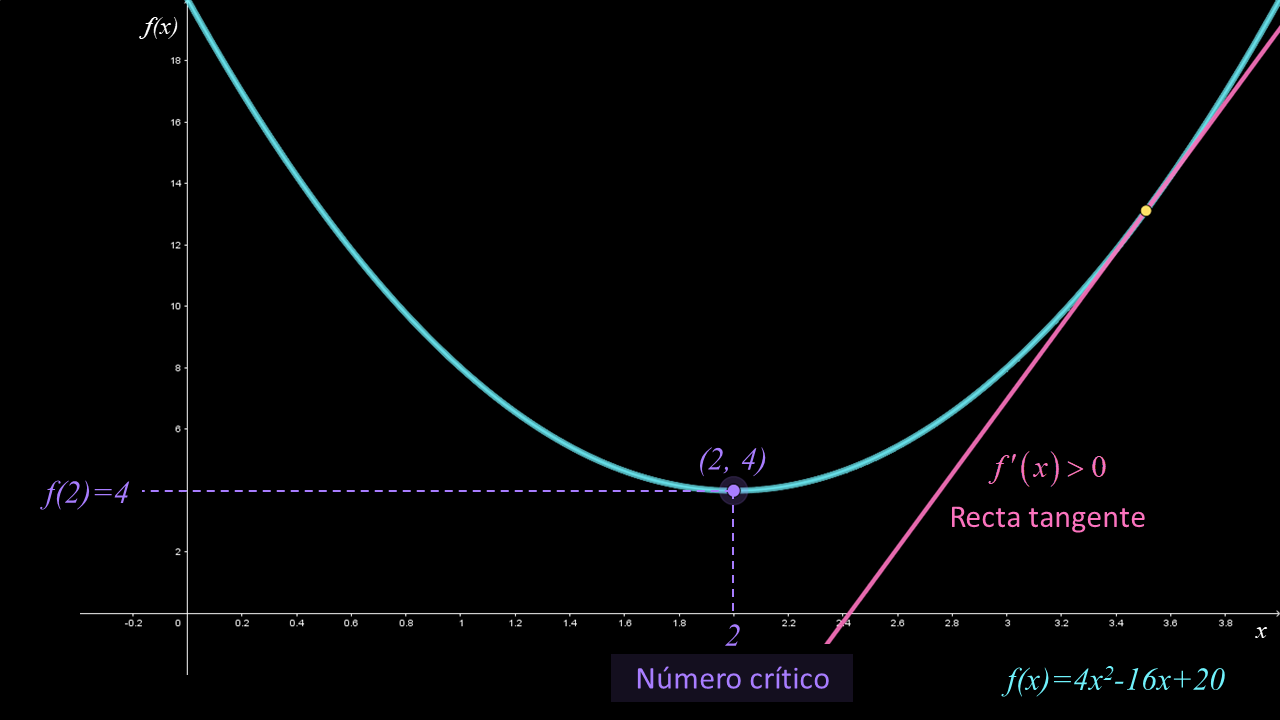
En las siguientes figuras se muestra la función $f\left( x \right) = 4{x^2} - 16x + 20$ con número crítico $x = 2$. De color rosa se muestra la recta tangente cuya pendiente es negativa para $x < 2$ y positiva para $x> 2$; en términos de derivadas se tiene que $f'\left( x \right) < 0$ para $x < 2$ y $f'\left( x \right)> 0$ para $x > 2$. En consecuencia, el signo de la deriva $f'\left( x \right)$ cambia de negativo a positivo en el número crítico $x = 2$.
Con base en las observaciones anteriores, podemos describir el comportamiento de la gráfica la función $f$:
• El número crítico es $x = 2$.
• Se tiene un punto crítico en $\left( {2,4} \right)$.
• En el intervalo $\left( { - \infty ,2} \right)$, la derivada de la función es negativa, es decir, $f'\left( x \right) < 0$.
• En el intervalo $\left( {2,\infty } \right)$, la derivada de la función es positiva, es decir, $f'\left( x \right) > 0$.
• En el número crítico, $f'$ cambia de negativo a positivo, entonces $f$ tiene un mínimo local en $x = 2$ (por el criterio de la primera derivada).
• En consecuencia, $f\left( 2 \right) = 4$ es un mínimo local.
-
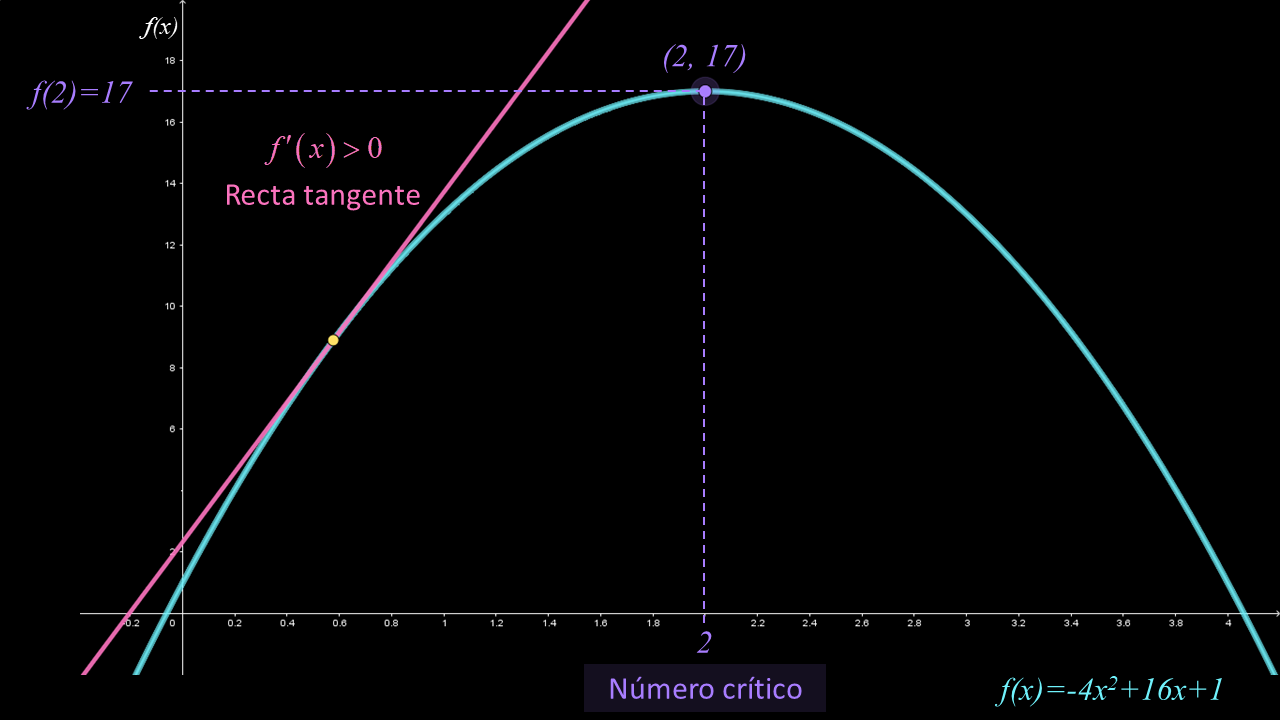
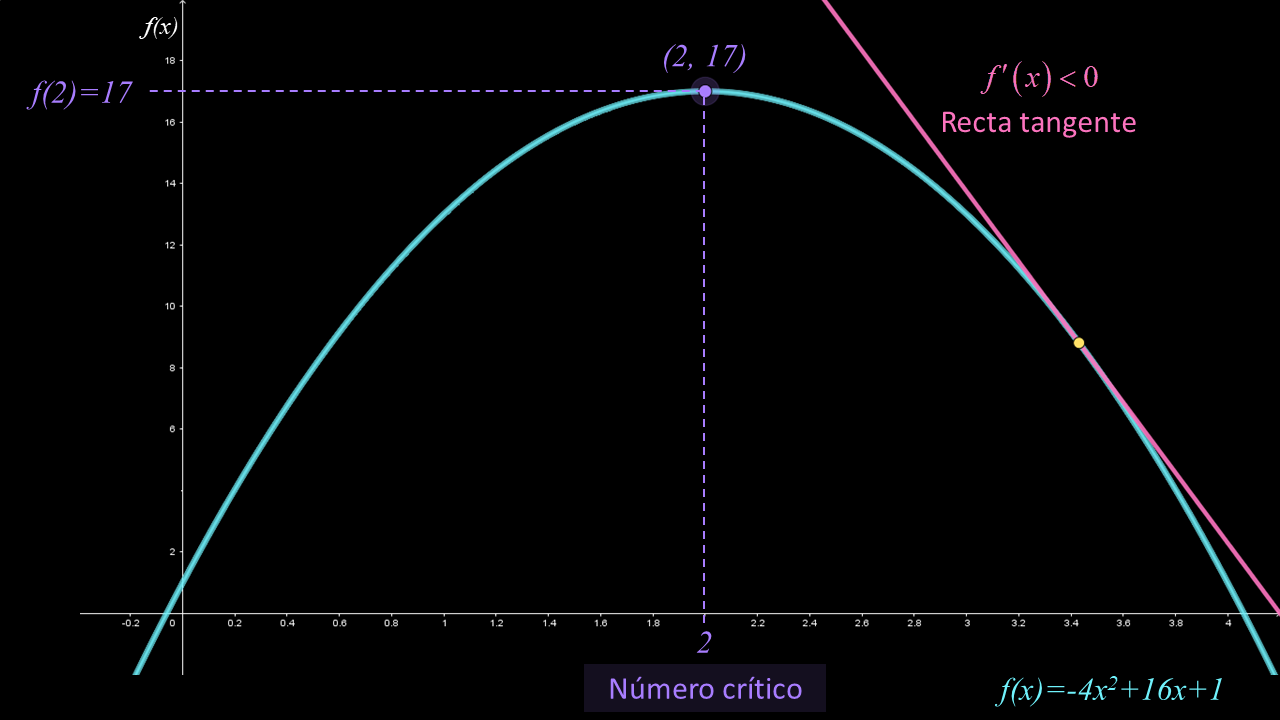
En las siguientes figuras se muestra la función $f\left( x \right) = - 4{x^2} + 16x + 1$ con número crítico $x = 2$. De color rosa se muestra la recta tangente cuya pendiente es positiva para $x < 2$ y negativa para $x> 2$; en términos de derivadas se tiene que $f'\left( x \right) > 0$ para $x < 2$ y $f'\left( x \right) < 0$ para $x> 2$. En consecuencia, el signo de la deriva $f'\left( x \right)$ cambia de positivo a negativo en el número crítico $x = 2$.
Con base en las observaciones anteriores, podemos describir el comportamiento de la gráfica la función $f$:
• El número crítico es $x = 2$.
• Se tiene un punto crítico en $\left( {2,17} \right)$.
• En el intervalo $\left( { - \infty ,2} \right)$, la derivada de la función es positiva, es decir, $f'\left( x \right) > 0$.
• En el intervalo $\left( {2,\infty } \right)$, la derivada de la función es negativa, es decir, $f'\left( x \right) < 0$.
• En el número crítico, $f'$ cambia de positivo a negativo, entonces $f$ tiene un máximo local en $x = 2$ (por el criterio de la primera derivada).
• En consecuencia, $f\left( 2 \right) = 17$ es un máximo local.
-
En el siguiente ejemplo se determinan los intervalos de crecimiento, así como valores máximos y mínimos locales de las siguientes funciones utilizando el criterio de la primera derivada.
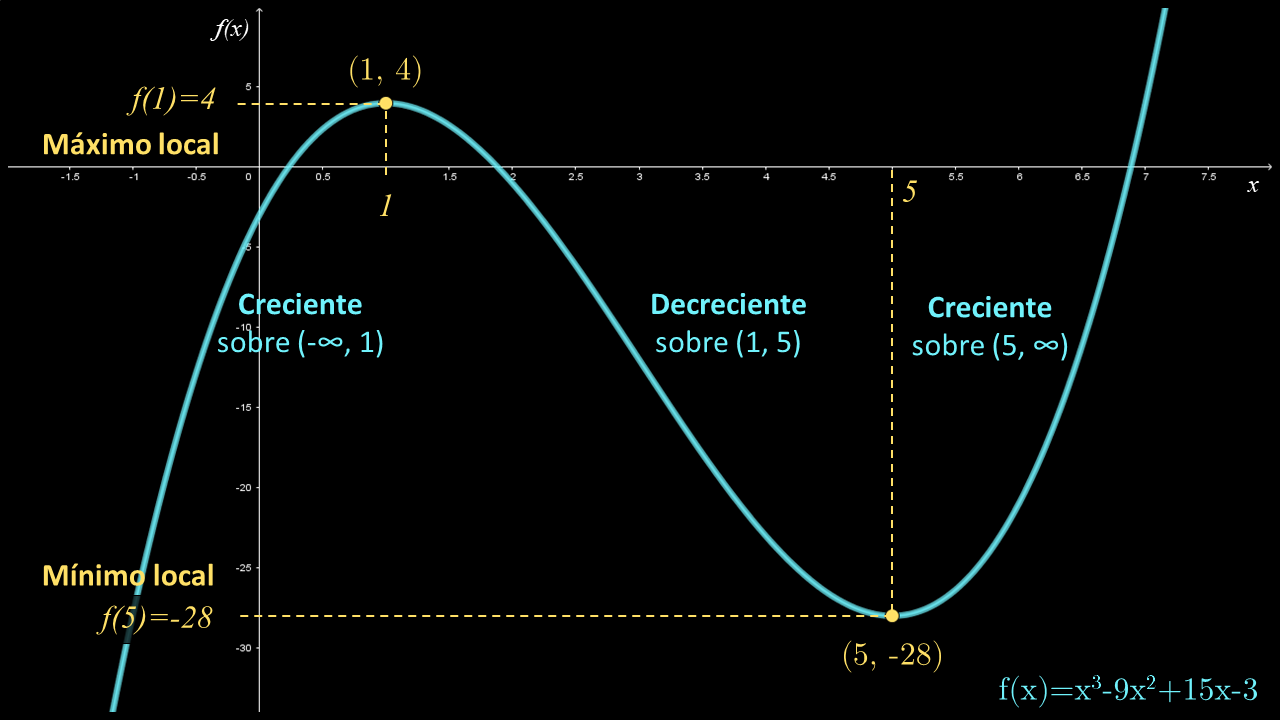
$f\left( x \right) = {x^3} - 9{x^2} + 15x - 3$
Primero se determina la derivada de $f$:
$f'\left( x \right) = 3{x^2} - 18x + 15 = 3\left( {{x^2} - 6x + 5} \right) = 3\left( {x - 5} \right)\left( {x - 1} \right)$
Después se encuentran los números críticos igualando la derivada a cero, es decir, $f'\left( x \right) = 0$:
$f'\left( x \right) = 3\left( {x - 5} \right)\left( {x - 1} \right) = 0$
La igualdad anterior se cumple en los números críticos $x = 1$ y $x = 5$; estos números dividen al dominio en tres intervalos: $\left( { - \infty ,1} \right)$, $\left( {1,5} \right)$ y $\left( {5,\infty } \right)$. Luego se calcula el signo de la derivada en cada intervalo para determinar si la función es creciente o decreciente en dichos intervalos; para ello, se escoge un número dentro de cada intervalo y se evalúa la deriva en él; el signo del valor de la derivada determina si la función es creciente o decreciente en el intervalo, según se indica en la siguiente tabla.
Intervalo Valor de la derivada $f'$ $f$ $\left( { - \infty ,1} \right)$ $f'\left( 0 \right) = 3\left( {\left( 0 \right) - 5} \right)\left( {\left( 0 \right) - 1} \right) = 15$ $+$ Creciente sobre $\left( { - \infty ,1} \right)$ $\left( {1,5} \right)$ $f'\left( 2 \right) = 3\left( {\left( 2 \right) - 5} \right)\left( {\left( 2 \right) - 1} \right) = - 9$ $-$ Decreciente sobre $\left( {1,5} \right)$ $\left( {5,\infty } \right)$ $f'\left( 6 \right) = 3\left( {\left( 6 \right) - 5} \right)\left( {\left( 6 \right) - 1} \right) = 15$ $+$ Creciente sobre $\left( {5,\infty } \right)$ A partir de la tabla anterior se puede concluir que:
• Como la derivada cambia de positiva a negativa en el número crítico $x = 1$, entonces la función tiene un valor máximo local en $x = 1$.
• Como la derivada cambia de negativa a positiva en el número crítico $x = 5$, entonces la función tiene un valor mínimo local en $x = 5$.
La siguiente gráfica confirma la información anterior.
Propósito. El desarrollo de los ejercicios te permitirá explorar la pendiente de la recta tangente y su relación con los máximos y mínimos de una función.
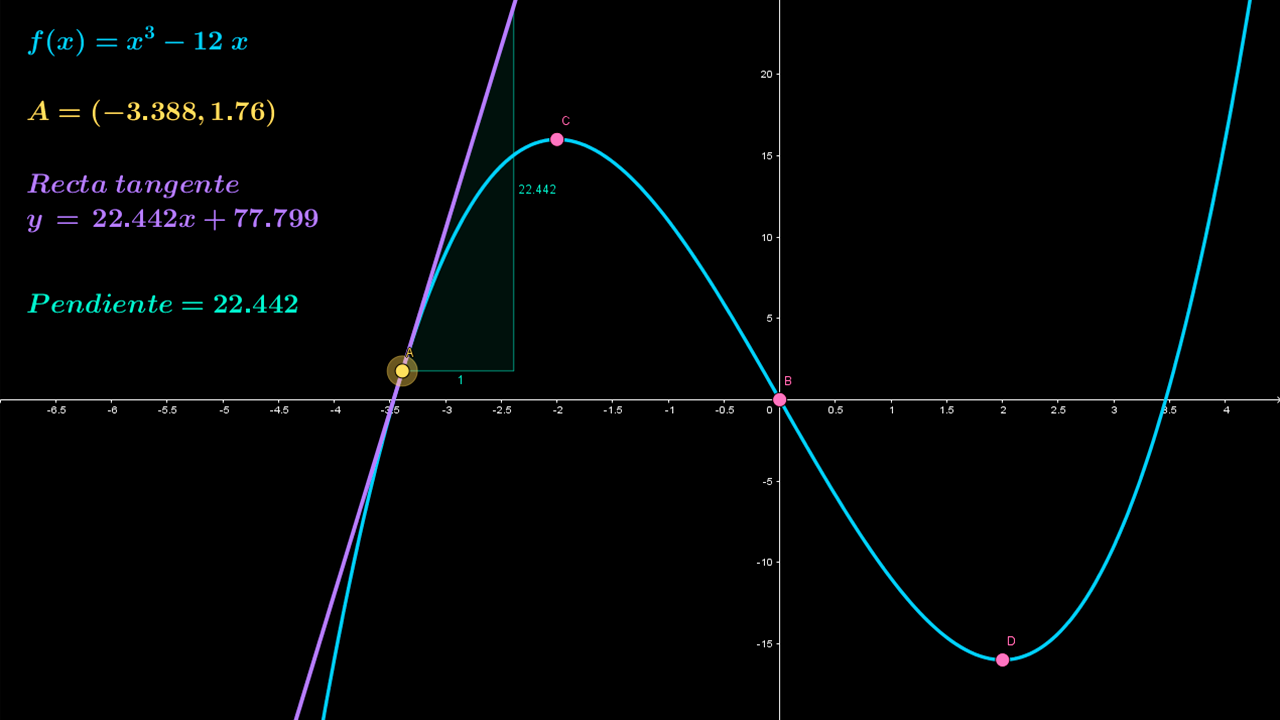
1. Analiza la gráfica de la función $f\left( x \right) = {x^3} - 12x$, así como la pendiente de la recta tangente en el punto A , y contesta las siguientes preguntas; revisa el recurso GeoGebra para realizar tu análisis.
Dada la función $f\left( x \right) = {x^2} - 2x + 11$, selecciona la opción correcta: