Solución de la forma ax2+c=d
Para comprender mejor el proceso de solución de la forma ax2+c=d se muestran tres ejemplos de ecuaciones cuadráticas, las cuales tienen la estructura de este tipo de forma. Da clic en cada pestaña para revisar los ejemplos:
Solución de la ecuación 2x2−18=0
Esta ecuación particular corresponde a la forma ax2+c=d con los valores a=2, c=−18 y d=0, al sustituir estos valores se tiene (2)x2+(−18)=(0) dando como resultado 2x2−18=0.
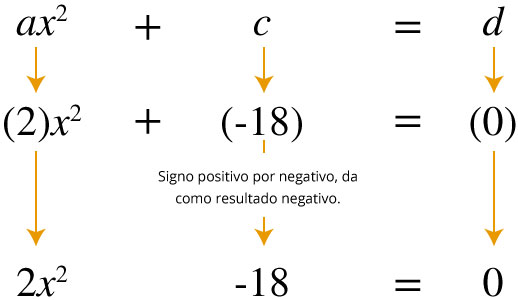
En el proceso para despejar la incógnita x, se aplican las mismas operaciones que sean pertinentes a los dos lados de la ecuación para conservar la igualdad y obtener ecuaciones equivalentes, es decir, ecuaciones que tengan las mismas soluciones.
A continuación se muestra el proceso detallado para llegar a la solución:
Revisa el proceso dando clic en los números
2x2−18=0
2x2−18=0
2x2−18+18=0+18
Sumar el parámetro independiente a los dos lados de la ecuación, que en este caso es 18.
2x2=18
Simplificar la ecuación.
2x2−18=0
2x2−18+18=0+18
2x2=18
2x22=182
Dividir entre el parámetro del término cuadrático a ambos lados de la ecuación, que en este caso es 2.
x2=9
Simplificar la ecuación.
2x2−18=0
2x2−18+18=0+18
2x2=18
2x22=182
x2=9
√x2=±√9
Extraer la raíz cuadrada a los dos lados de la ecuación, con valores positivo y negativo.
x=±√9
Simplificar la ecuación.
2x2−18=0
2x2−18+18=0+18
2x2=18
2x22=182
x2=9
√x2=±√9
x=±√9
x=±3
Simplificar los valores restantes.
2x2−18=0
2x2−18+18=0+18
2x2=18
2x22=182
x2=9
√x2=±√9
x=±√9
x=±3
x1=3
Se obtiene la solución 1 , tomando el signo positivo.
x2=−3
Se obtiene la solución 2 , tomando el signo negativo.
Para distinguir los dos valores de x que se obtienen como solución de la ecuación, se le puede poner un subíndice a x:
x1=3
x1=−3
Comprobación
Para verificar que las soluciones encontradas son correctas, se sustituye cada solución en la ecuación original, al resolverla se corrobora que se cumpla la igualdad, como se muestra a continuación:
Para x1=3
2x2−18=0
2(3)2−18=0
2(9)−18=0
18−18=0
0=0
Para x2=−3
2x2−18=0
2(−3)2−18=0
2(9)−18=0
18−18=0
0=0
Como se cumple la igualdad, las soluciones encontradas son correctas.
Solución de la ecuación 3x2+2=50
Esta ecuación también responde a la forma ax2+c=d, sólo que en este caso la ecuación se muestra con signo positivo, a diferencia del ejemplo 1 que se presentaba con signo negativo, pero como tiene la misma estructura el procedimiento es el mismo, a continuación se detalla:
Revisa el proceso dando clic en los números
3x2+2=50
3x2+2=50
3x2+2−2=50−2
Con la finalidad de despejar el término cuadrático se resta 2 en ambos lados de la ecuación.
3x2=48
Simplificar la ecuación.
3x2+2=50
3x2+2−2=50−2
3x2=48
3x23=483
Para continuar el despeje de la variable x se divide entre 3 los dos lados de la ecuación.
x2=16
Simplificar la ecuación.
3x2+2=50
3x2+2−2=50−2
3x2=48
3x23=483
x2=16
√x2=±√16
Extrae la raíz cuadrada a los dos lados de la ecuación, tomando los valores positivo y negativo de la raíz.
x=±4
Simplificar la ecuación.
x1=4
Se obtiene la solución 1 , tomando el signo positivo.
x2=−4
Se obtiene la solución 2 , tomando el signo negativo.
Comprobación
Se verifica que las soluciones encontradas sean correctas sustituyendo cada solución en la ecuación original 3x^2+2=50 y corroborando que se cumpla la igualdad:
Para x1=4
3x2+2=50
3(4)2+2=50
3(16)+2=50
48+2=50
50=50
Para x2=−4
3x2+2=50
3(−4)2+2=50
3(16)+2=50
48+2=50
50=50
Como se cumple la igualdad, las soluciones encontradas son correctas.
Solución de la ecuación x2+13=4
Esta ecuación también responde a la forma ax2+c=d con los valores: a=1 , c=13 y d=4 , ya que al sustituir estos valores en éste se tiene (1)x2+(13)=(4) y resulta x2+13=4.
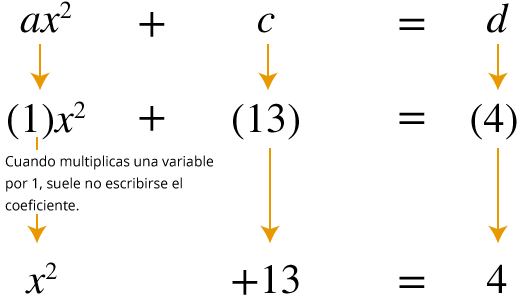
Para despejar la incógnita x se invierten las operaciones que contiene la ecuación, obteniendo ecuaciones equivalentes cada vez más simples hasta llegar a la solución.
En los números reales no existe raíz cuadrada de un número negativo, pero sí en los números complejos, donde i=√−1 es la unidad imaginaria, por ejemplo: i=√−4=√4(−1)=(√4)(√−1)=(2)(i)=2i.
Una ecuación de segundo grado puede no tener solución en los números reales, pero sí en los números complejos. Los números complejos son de la forma z=a+bi, donde a y b son números reales, a es la parte real del número complejo y b es su parte imaginaria. Un ejemplo de un número complejo es z=3+2i.
A continuación se muestra el procedimiento para resolver la ecuación x2+13=4 la cual contiene en su solución números complejos, obsérvala con atención.
Revisa el proceso dando clic en los números
x2+13=4
x2+13=4
x2+13−13=4−13
Con la intención de despejar el término cuadrático se resta 13 a los dos lados de la ecuación.
x2=−9
Simplificar la ecuación.
x2+13=4
x2+13−13=4−13
x2=−9
√x2=±√−9
Se extrae la raíz cuadrada a los dos lados de la ecuación, tomando los valores positivo y negativo.
x2+13=4
x2+13−13=4−13
x2=−9
√x2=±√−9
x=±3i
Simplificando se obtiene una raíz imaginaria, ya que √−9=√(9)(−1)=(√9)(√−1)=3i, con i=√(−1).
x1=3i
Se obtiene la solución 1 , tomando el signo positivo.
x2=−3i
Se obtiene la solución 2 , tomando el signo negativo.
Comprobación
Para comprobar que las soluciones encontradas son correctas, se sustituye cada una en la ecuación original x2+13=4 y se verifica que se cumpla la igualdad:
Para x1=3i
x2+13=4
(3i)2+13=4
(3)2i2+13=4
9i2+13=4
9(√−1)2+13=4
9(−1)+13=4
−9+13=4
4=4
Para x2=−3i
x2+13=4
(−3i)2+13=4
(−3)2i2+13=4
9i2+13=4
9(√−1)2+13=4
9(−1)+13=4
−9+13=4
4=4
Como se cumple la igualdad, las soluciones encontradas son correctas.


