Problema de Cinemática 1: La parábola de Jordan
El ex jugador de baloncesto de la NBA, Michael Jordan fue famoso por sus saltos pues parecía mantenerse suspendido en la altura máxima de su salto mientras se dirigía hacia la canasta del equipo contrario; el movimiento de su cuerpo describía una parábola muy alargada, al igual que el balón sostenido por él.
Los diferentes niveles de altura que alcanzaba el balón sostenido por Michael Jordan se pueden calcular mediante una expresión matemática conocida como ecuación de movimiento. Ésta es una ecuación cuadrática que permite calcular la altura (h) alcanzada por el balón después de cierto tiempo (t) y está determinada por:
Revisa el proceso dando clic en los números
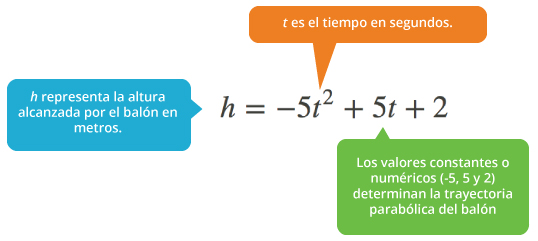
En donde h se expresa en metros (m) y t en segundos (s).
Para calcular la altura que alcanza el balón después de cierto tiempo basta con sustituir este parámetro en la ecuación de movimiento y realizar las operaciones necesarias. Por ejemplo, si deseas encontrar la altura alcanzada por el balón después de t = 0.4 [s] se realizan las operaciones que resultan de sustituir el tiempo en la ecuación de movimiento, es decir:
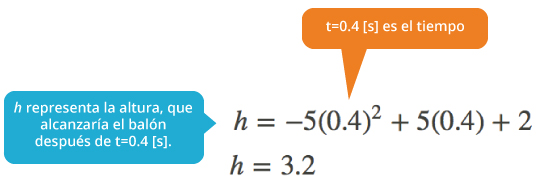
Por lo tanto, al transcurrir 0.4 segundos se tiene que el balón alcanza una altura de 3.2 metros.
La ecuación de movimiento también te permite calcular el tiempo transcurrido para que el balón alcance cierta altura. Para ello se requiere sustituir el valor de la altura en la ecuación correspondiente y el tiempo se determina mediante alguno de los métodos de factorización o por medio de la fórmula general.
Por ejemplo, si se desea determinar el tiempo que transcurre para que el balón alcance una altura de 2.8 metros (h = 2.8) entonces, al sustituir el valor de la altura en la ecuación de movimiento, se obtiene la siguiente expresión:
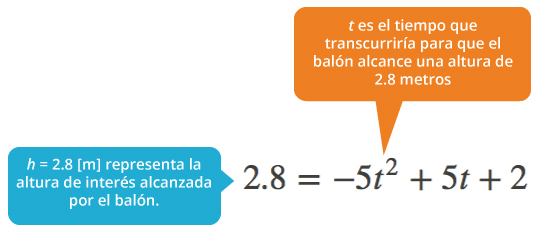
Al reordenar los términos de la expresión anterior entonces se obtiene una ecuación cuadrática de la forma $at^2+bt+c=0$, es decir:

Las raíces de la ecuación cuadrática anterior corresponden al tiempo que transcurre para que el balón alcance una altura de 2.8 metros. Tales raíces son:
$$ t_1 = 0.2 [s] $$
$$ t_2 = 0.8 [s] $$
Puedes encontrar las raíces utilizando la fórmula general.
La existencia de dos raíces representa los dos instantes de tiempo en los que el balón alcanzará la altura de 2.8 metros: durante el ascenso ($t=0.2 [s]$) y en el descenso ($t=0.8 [s]$).

En el siguiente material de Geogebra se te presenta una animación que describe la trayectoria parabólica del balón, en donde se indican las diferentes alturas que éste alcanza en diferentes instantes de tiempo. Asimismo, encontrarás dos ejercicios en las pestañas del lado derecho. Desarrolla las operaciones correspondientes en tu cuadero y escribe en Geogebra el resultado.


