Los problemas de tu entorno cotidiano relacionados con el cálculo de áreas pueden solucionarse con la modelación de una ecuación cuadrática. A continuación te mostramos cómo.
Problema. Los vacacionistas del hotel Mayan Palace tienen acceso al mar para refrescarse, para su seguridad los empleados del mismo delimitan con una cuerda con boyas un área rectangular de 600 metros cuadrados, considerando que el largo tiene 10 metros más que el ancho. Determina la longitud del ancho y del largo.
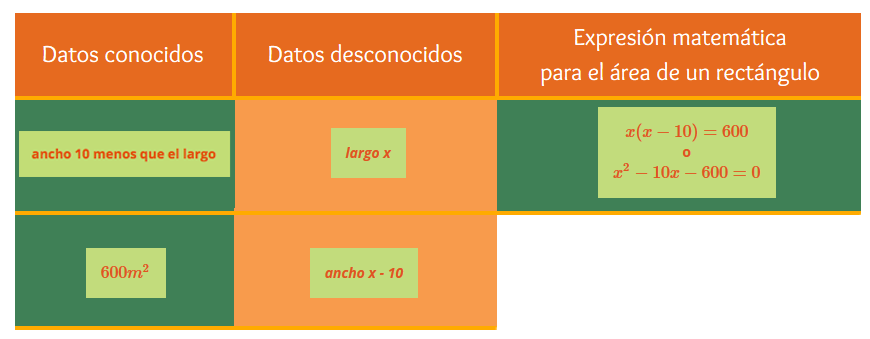
Para una mejor comprensión del problema se presenta su modelo geométrico y la relación entre los datos y las incógnitas mediante una ecuación de segundo grado y su resolución por el método de tabulación.

Modelo geométrico:
- x(x−10)=600
o
x2−10x−600=0 - 600m2
- largo x
- ancho x - 10
- ancho 10 menos que el largo
| Datos conocidos | Datos desconocidos | Expresión matemática para el área de un rectángulo |
Las opciones correctas se han marcado en color verde, las incorrectas en color rojo.
Respuestas correctas: