Problema viaje
Los problemas abordados con anterioridad hacen referencia a problemas de áreas. Para mostrar otros campos de aplicación de las ecuaciones cuadráticas, a continuación se presentan problemas relacionados con el cálculo de costos.
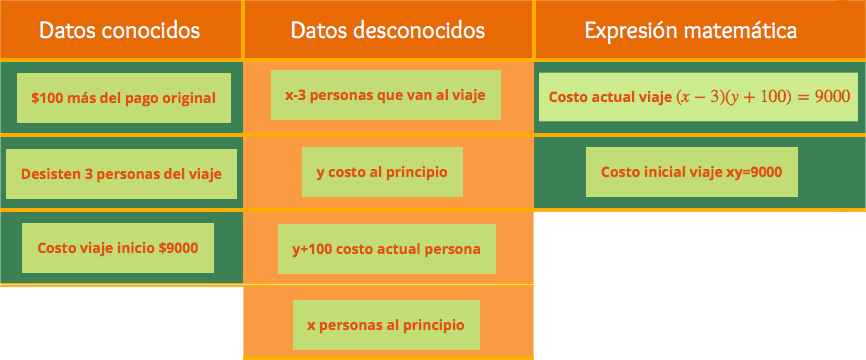
Problema. El transporte para una excursión con x personas tiene un costo de 9000. El costo por persona para el viaje es y pesos, si desisten tres personas, cada una de las personas restantes tendría que pagar 100 más. Obtén el número de personas que van a la excursión y determina la cantidad que paga cada una.

- Con base en el problema propuesto, identifica los datos conocidos, desconocidos y la relación entre ellos, mediante una ecuación de segundo grado. Arrástralos a los recuadros de la tabla según corresponda.
- Costo viaje inicio $9000
- x personas al principio
- Desisten 3 personas del viaje
- y+100 costo actual persona
- Costo inicial viaje xy=9000
- $100 más del pago original
- x-3 personas que van al viaje
- y costo al principio
- Costo actual viaje $(x-3)(y+100)=9000$
| Datos conocidos | Datos desconocidos | Expresión matemática |
Las opciones correctas se han marcado en color verde, las incorrectas en color rojo.
Respuestas correctas:
Luego de establecer la relación entre datos, hay que obtener la ecuación cuadrática. A continuación se muestra cómo.
$xy=9000$ (1)
Ecuación costo viaje
$(x-3)(y+100)=9000$ (2)
Ecuación costo viaje al desistir 3 personas
$ y= \frac{9000}{x}$
Despejar y de la ecuación 1
$(x-3)(\frac{9000}{x}+100)=9000$ (3)
Sustituir y en la ecuación 2
$(x-3)(\frac{9000}{x})+100(x-3)=9000$
Eliminar segundo paréntesis. Cada uno de sus términos se multiplica por (x – 3)
$(x)[(x-3)(\frac{9000}{x}) +100(x-3)=9000]$
Multiplicar por x a la ecuación para eliminar la x del denominador
$ x(x-3)(\frac{9000}{x})+100x(x-3)=9000x$
Eliminar el corchete. Cada expresión en éste, se multiplica por x
$(x-3)(9000)+100x(x-3)=9000x$
Resultado al considerar $\frac {x}{x}=1$
$9000x-27000+100x^2-300x=9000x$
Eliminar los paréntesis
$9000x-27000+100x^2-300x-9000x=9000x-9000x$
Restar 9000x a los lados de la ecuación
$100x^2-300x-27000=0$
Ecuación cuadrática, obtenida al simplificar los lados de la ecuación
$x^2-3x-270=0$
Dividir la ecuación entre 100 para reducirla y facilitar la solución
Recuerda que la ecuación también puede resolverse utilizando la fórmula general, o mediante los métodos de factorización y de trinomio cuadrado perfecto.



