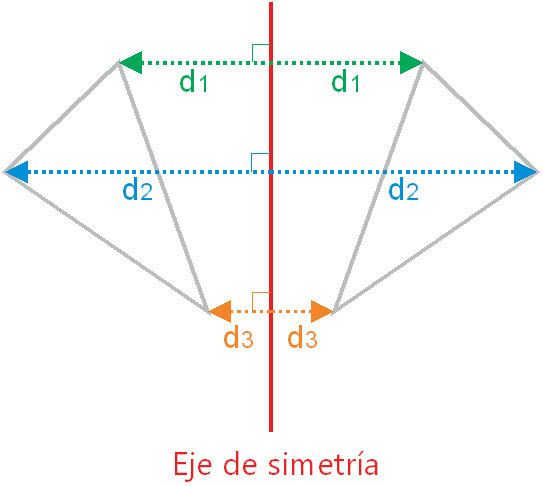
Interpretación del discriminante de una ecuación de segundo grado
A partir de una función cuadrática o de segundo grado o cuya expresión es $y=ax^2+bx+c$, podemos igualar la función a un valor determinado que sea paralelo al eje x. Regularmente se iguala a cero. Esta operación da origen a la ecuación cuadrática siguiente:
$$ax^2+bx+c=0$$
Dichas soluciones, también conocidas como raíces o ceros, corresponden a la intersección de la función con el eje de las abscisas. A los coeficientes a, b y c se les conoce como parámetros de la ecuación.
Las raíces de la ecuación de segundo grado se obtienen mediante la fórmula general:
$$x=\frac{-b\pm{}\sqrt{b^2-4ac}}{2a}$$
A la expresión que se ubica dentro de la raíz cuadrada se le conoce como discriminante (representada con una d):
$$d=b^2-4ac$$
El valor del discriminante determina tres situaciones que se presentan al calcular su raíz cuadrada:
| d | > 0 | Existen dos soluciones reales, derivadas de los dos signos (+ y –) del radical. |
| = 0 | Existen dos soluciones iguales, ya que el término que se suma y resta es cero; suele decirse que tiene solución única de multiplicidad 2. | |
| < 0 | No existe solución en los números reales, pero sí en los números complejos. |
Las situaciones anteriores se detallan a continuación. Da clic en cada pestaña del acordeón
Tal como su nombre lo indica, las ecuaciones de segundo grado tienen dos soluciones; cuando el discriminante es positivo, la ecuación puede reducirse a las siguientes expresiones:
$$x_1=\frac{-b+\sqrt{b^2-4ac}}{2a}$$
$$x_2=\frac{-b-\sqrt{b^2-4ac}}{2a}$$
Lo anterior indica que si graficamos la función $y=ax^2+bx+c$ se tendrá que la gráfica cruzará el eje X en dos puntos (cuando igualamos a $y=0$) de acuerdo a la fórmula general. Ambas soluciones son simétricas, respecto al eje de simetría $x=\frac{-b}{2a}$ de la gráfica de la función, se ubican a una cantidad $\frac{\sqrt{b^2-4ac}}{2a}$ a ambos lados de $x=\frac{-b}{2a}$ como se muestra a continuación:
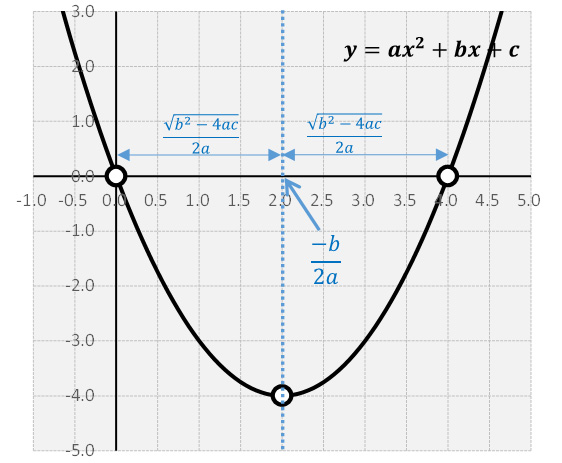
Ejemplo: Considera la ecuación $y=x^2-4x$, tenemos que los parámetros de la ecuación son $a=1$, $b=-4$ y $c=0$.
El valor del discriminante es $d={(-4)}^2-4(1)(0)=16-0=16$
El discriminante es positivo. Por lo tanto, se tendrán dos soluciones reales:
$x_1=\frac{-(-4)+\sqrt{{(-4)}^2-4(1)(0)}}{2(1)}=\frac{4+\sqrt{16-0}}{2}=$ $\frac{4+4}{2}=\frac{8}{2}=4$
$x_2=\frac{-(-4)-\sqrt{{(-4)}^2-4(1)(0)}}{2(1)}=\frac{4-\sqrt{16-0}}{2}=$ $\frac{4-4}{2}=\frac{0}{2}=0$
De acuerdo con la fórmula general, cuando el discriminante es = 0, las soluciones de la ecuación pueden reducirse a la siguiente expresión:
$$x_1=\frac{-b+\sqrt{0}}{2a}=\frac{-b}{2a}$$
$$x_2=\frac{-b-\sqrt{0}}{2a}=\frac{-b}{2a}$$
$$x_1=x_2=\frac{-b}{2a}$$
En esta solución, $x_1=x_2$ Al graficar una función con discriminante = 0, la gráfica tocará sólo una vez el eje X, en el valor $x=\frac{-b}{2a}$ como se muestra a continuación:
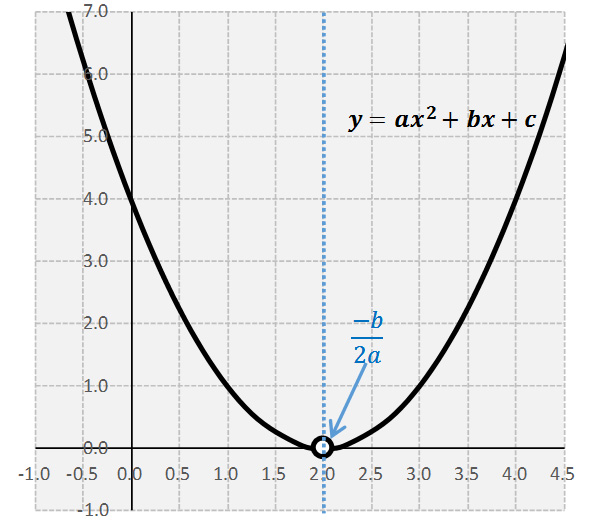
Ejemplo: Considera la ecuación $y=x^2-4x+4$ Tenemos que los parámetros de la ecuación son $a=1$, $b=-4$ y $c=4$.
El valor del discriminante es $d={(-4)}^2-4(1)(4)=16-16=0$
El discriminante es igual a cero, por lo tanto, se tendrán dos soluciones reales iguales (solución “única”):
$x_1=\frac{-(-4)+\sqrt{{(-4)}^2-4(1)(4)}}{2(1)}=\frac{4+\sqrt{16-16}}{2}=$ $\frac{4+0}{2}=\frac{4}{2}=2$
$x_2=\frac{-(-4)-\sqrt{{(-4)}^2-4(1)(4)}}{2(1)}=\frac{4-\sqrt{16-16}}{2}=$ $\frac{4-0}{2}=\frac{4}{2}=2$
Observa que $x_1=x_2=2$
De acuerdo con la fórmula general, cuando el discriminante < 0, las soluciones de la ecuación pueden reducirse a la siguiente expresión:
$$ x_1 = \frac {-b + \sqrt{d}} {2a} $$
Si $ d = b^2 -4ac $ es un número negativo no será posible obtener la raíz cuadrada del discriminante, recuerda que al multiplicar una cantidad por –1 dos veces, el resultado es uno: 1=(–1)(–1), aplicando esta identidad al interior del radical tendremos:
$$ x_1 = \frac {-b + \sqrt{d(-1)(-1)}} {2a} $$
Reagrupando el radical:
$$ x_1 = \frac {-b + \sqrt{(-d)(-1)}} {2a} $$
Aplicando la propiedad de distributividad de la multiplicación con las potencias y los radicales, podemos separar los términos al interior del radical de la siguiente forma:
$$ x_1 = \frac {-b + \sqrt{(-d) } \sqrt {(-1)}} {2a} = \frac {-b + \sqrt{-d } \sqrt {-1}} {2a} $$
Recuerda que d es negativo, por lo que en este momento ya es posible calcular $ \sqrt {-d} $. Por otro lado la definición del número imaginario $ i = \sqrt {-1} $ se sustituye en la expresión anterior:
$$ x_1 = \frac {-b + \sqrt {-d} (i) } {2a} $$
Aplicando la distributividad en la división podemos separar la suma del numerador en dos términos:
$$ x_1 = \frac {-b } {2a} + \frac {\sqrt {-d}(i) } {2} $$
O reacomodando el segundo término de la expresión:
$$ x_1 = \frac {-b } {2a} + \frac {\sqrt {-d} } {2} i $$
El grado de la ecuación es 2, indica que habrá dos soluciones en los números complejos, en forma práctica, este hecho nos indica que la gráfica no intersecta al eje X.
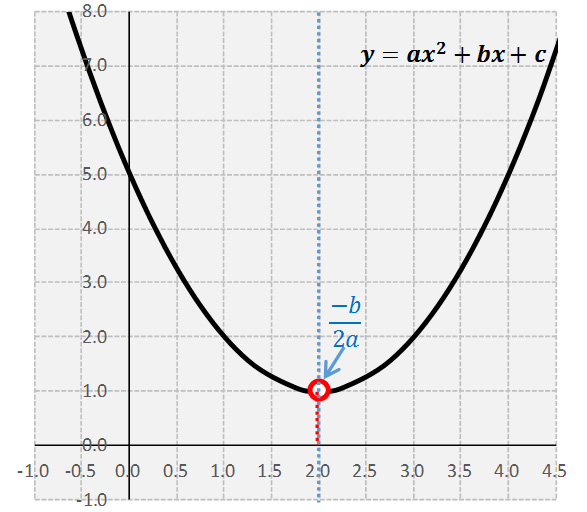
Ejemplo: Considera la ecuación $y=x^2-4x+5$, tenemos que los parámetros de la ecuación son $a=1$, $b=-4$ y $c=5$.
El valor del discriminante es $d={(-4)}^2-4(1)(5)=16-20=-4$
El valor del discriminante es negativo, por lo tanto, se tendrán dos soluciones complejas:
Considerando el signo positivo:
$$ x_1= \frac {-(-4) + \sqrt {(-4)^2 - 4(1)(5)} } { 2(1)} $$
$$ x_1= \frac {4 + \sqrt {16 - 20} } { 2} $$
$$ x_1= \frac {4 + \sqrt {-4} } { 2} $$
$$ x_1= \frac {4 + \sqrt {-4(-1)(-1)} } { 2 } $$
$$ x_1= \frac {4 + \sqrt {4} \sqrt{-1} } { 2 } $$
$$ x_1= \frac {4 + 2i } { 2 } $$
Finalmente:
$$ x_1= 2 + i $$
Considerando el signo negativo:
$$ x_2= \frac {-(-4) - \sqrt {(-4)^2 - 4(1)(5)} } { 2(1)} $$
$$ x_2= \frac {4 - \sqrt {16 - 20} } { 2} $$
$$ x_2= \frac {4 - \sqrt {-4} } { 2} $$
$$ x_2= \frac {4 - \sqrt {-4(-1)(-1)} } { 2 } $$
$$ x_2= \frac {4 - \sqrt {4} \sqrt{-1} } { 2 } $$
$$ x_2= \frac {4 - 2i } { 2 } $$
Finalmente:
$$ x_2= 2 - i $$
En las tres soluciones se puede observar que la gráfica es simétrica y cambia de dirección en el punto $x=\frac{-b}{2a}$, la gráfica abrirá hacia arriba si el parámetro a es positivo y abrirá hacia abajo si el parámetro es negativo.
Conclusiones
Es importante notar que para que el discriminante no sea menor que cero, debe cumplirse que $b^2-4ac>0$, por lo que al hacer el despeje, se debe cumplir la condición $b^2>4ac$.
De lo anterior puede observarse que: