Problema 1
Para medir la longitud inaccesible $\overline{DE}$, un agrimensor se posicionó en el punto $C$ y midió la longitud del segmento $\overline{DC}$ y lo prolongó hasta el punto $B$, tal que $\overline{DC} \cong \overline{CB}$, luego midió el segmento $\overline{EC}$ y lo prolongó hasta el punto $A$, tal que $\overline{EC} \cong \overline{CA}$. El agrimensor mide $\overline{AB}$ y afirma que $\overline{DE} \cong \overline{AB}$, puesto que $\bigtriangleup ACD \cong \bigtriangleup ACD$. Demuestra la validez del método utilizado en la construcción.
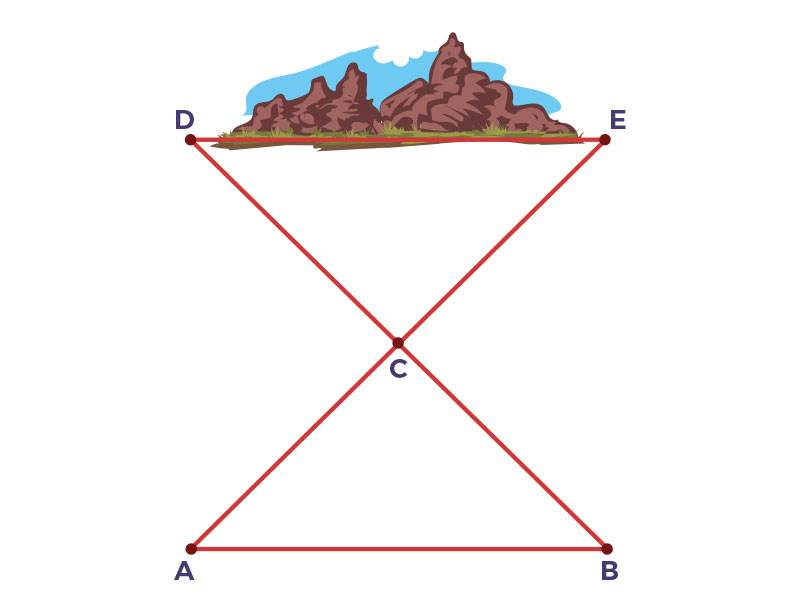 |
Hipótesis: $\overline{DC} \cong \overline{CB}$ y $\overline{EC} \cong \overline{CA}$ Tesis: $\bigtriangleup ABC \cong \bigtriangleup CDE$ |
| Proposiciones | Razones |
| $ \overline {DC} \cong \overline {CB}$ | Por hipótesis. |
| Teorema. Los ángulos opuestos por el vértice son congruentes. | |
| $\overline {EC} \cong \overline {CA}$ | Por hipótesis. |
| $\bigtriangleup CDE \cong \bigtriangleup ABC$ | |
| Las partes correspondientes de triángulos congruentes son congruentes (paso 4). |
| Proposiciones | Razones |
| $ \overline {DC} \cong \overline {CB}$ | Por hipótesis. |
| $ \sphericalangle DCB\cong\sphericalangle ACB$ | Teorema. Los ángulos opuestos por el vértice son congruentes. |
| $\overline {EC} \cong \overline {CA}$ | Por hipótesis. |
| $\bigtriangleup CDE \cong \bigtriangleup ABC$ | Criterio de congruencia LAL. |
| $\overline {DE}\cong{\overline {AB}}$ | Las partes correspondientes de triángulos congruentes son congruentes (paso 4). |
Problema 2
Demuestra que los triángulos $\bigtriangleup ABC \cong \bigtriangleup ACD$ con la hipótesis que se especifica.
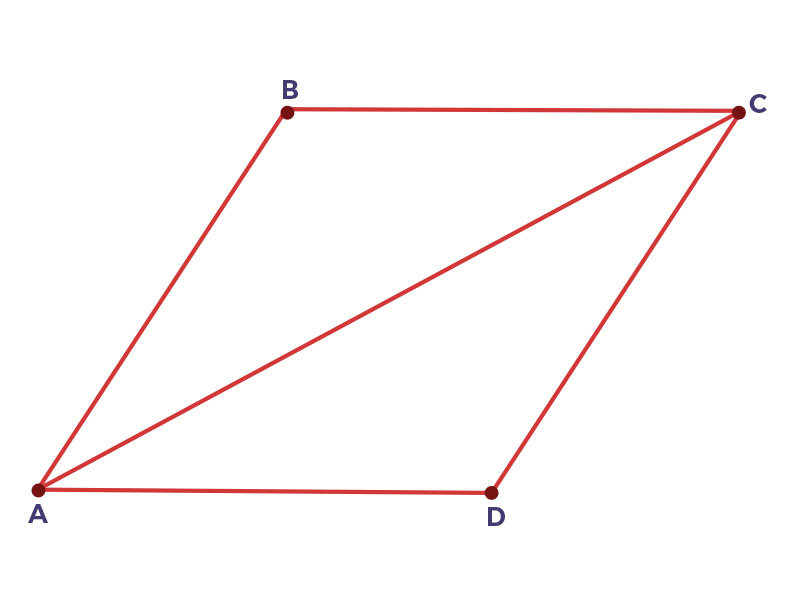 |
Hipótesis: $\overline {AB} \cong \overline {CD}$ y $\overline {BC} \cong \overline {AD}$ Tesis: $\bigtriangleup ABC \cong \bigtriangleup ACD$ |
| Proposiciones | Razones |
| $\overline {AB} \cong \overline {CD}$ | Por hipótesis. |
| $\overline {BC} \cong \overline {AD}$ | |
| Postulado. Toda figura geométrica es congruente a sí misma. | |
| $\bigtriangleup CDE \cong \bigtriangleup ABC$ |
| Proposiciones | Razones |
| $\overline {AB} \cong \overline {CD}$ | Por hipótesis. |
| $\overline {BC} \cong \overline {AD}$ | Por hipótesis. |
| $\overline {AC} \cong{\overline {AC}}$ | Postulado. Toda figura geométrica es congruente a sí misma. |
| $\bigtriangleup CDE \cong \bigtriangleup ABC$ | Criterio de congruencia LLL |
Problema 3 mt-2
Si $\sphericalangle CAB \cong \sphericalangle BAD$ y $\measuredangle ABC\cong \measuredangle ABD$, demuestra que $\bigtriangleup ABC \cong \bigtriangleup ABD$.
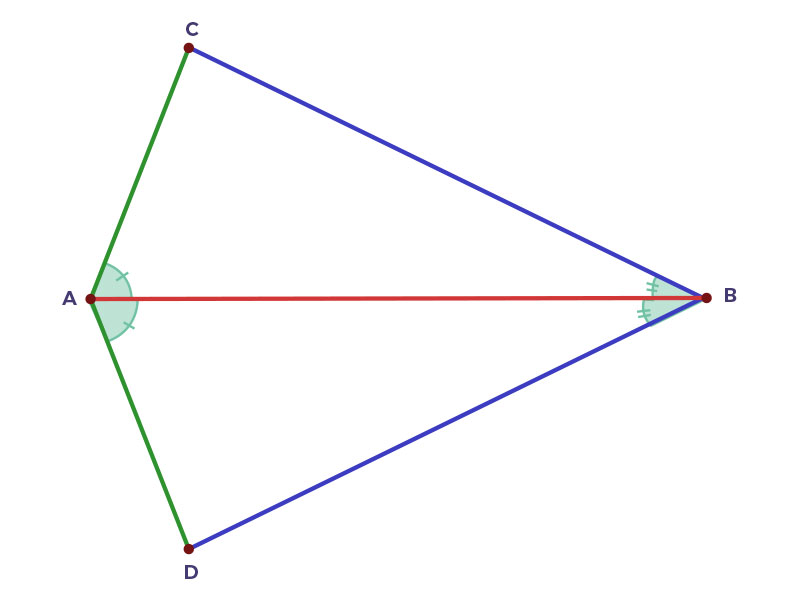 |
Hipótesis: $\sphericalangle CAB \cong \sphericalangle BAD$ y $\measuredangle ABC\cong \measuredangle ABD$ Tesis: $\bigtriangleup ABC \cong \bigtriangleup ABD$ |
| Proposiciones | Razones |
| 1. $\sphericalangle CAB \cong \sphericalangle BAD$ | |
| 2. | Postulado. Toda figura geométrica es congruente así misma. |
| 3. $\sphericalangle ABC \cong \sphericalangle ABD$ | Por hipótesis. |
| 4. $\bigtriangleup ABC \cong \bigtriangleup ABD$ |
| Proposiciones | Razones |
| 1. $\sphericalangle CAB \cong \sphericalangle BAD$ | Por hipótesis. |
| 2. ${\overline {AB} \cong \overline {AB}}$ | Postulado. Toda figura geométrica es congruente así misma. |
| 3. $\sphericalangle ABC \cong \sphericalangle ABD$ | Por hipótesis. |
| 4. $\bigtriangleup ABC \cong \bigtriangleup ABD$ | Criterio de congruencia ALA. |
Problema 4
Los triángulos $\bigtriangleup ADE$ y $\bigtriangleup BCE$ son congruentes. Determina el valor de $x e y$.


