En este apartado se profundiza el estudio de la congruencia de triángulos, así como, sus criterios de congruencia, los cuales serán utilizados en la demostración de algunas construcciones con regla y compás; y en su aplicación a la solución de problemas.

Al interactuar con recursos GeoGebra comprenderás los criterios de congruencia de triángulos: Lado-Ángulo-Lado (LAL); Ángulo-Lado-Ángulo (ALA) y Lado-Lado-Lado (LLL), así como su fundamentación empírica para poder aplicarlo en la resolución de problemas de corte geométrico. Lo anterior te permitirá concluir que la congruencia de triángulos requiere únicamente la congruencia de tres de sus partes correspondientes (homólogas). La demostración de estos criterios se hará de forma empírica, al hacer coincidir dos triángulos en todas sus partes, cuando esto sucede los triángulos son congruentes y como consecuencia también lo son sus partes correspondientes.

En este criterio se presenta un recurso GeoGebra con dos triángulos que tienen dos lados y el ángulo comprendido congruentes. Mediante tu interacción con el recurso descubrirás regularidades que presentan sus partes homólogas para que formules el criterio de congruencia de triángulos LAL.
Según la exploración del recurso y las regularidades que identificaste en la sobreposición del $\bigtriangleup PQR$ sobre el $\bigtriangleup ABC$, contesta la pregunta ¿$\bigtriangleup ABC \cong \bigtriangleup PQR$?, (sí o no) la respuesta escríbela en el recuadro.
Con base en los supuestos de que dos triángulos tienen dos lados y el ángulo comprendido entre ellos, respectivamente congruentes, se establece la formulación del criterio de congruencia de triángulos LAL.
Formulación del criterio de la congruencia de triángulos LAL
Si dos lados y el ángulo incluido de un triángulo son congruentes con dos lados y el ángulo incluido de otro triángulo, entonces los triángulos son congruentes.
Demostración empírica del criterio de congruencia de triángulos LAL.
Como los triángulos $\bigtriangleup ABC$ y $ \bigtriangleup PQR$ coinciden en todos sus puntos, se concluye que son triángulos congruentes y que sus partes correspondientes también lo son, es decir, sus ángulos correspondientes tienen la misma medida y sus lados correspondientes la misma longitud, tal como, pudiste apreciar al activar la casilla de control Tesis congruencia LAL.
Considerando que $\bigtriangleup ABC \cong \bigtriangleup PQR$, arrastra a la siguiente tabla la congruencia que hace falta para completarla.
| Ángulos correspondientes | $\sphericalangle \alpha \cong \sphericalangle \delta$ | $\sphericalangle \gamma \cong \sphericalangle \zeta$ | |
| Lados correspondientes | $\overline{AB} \cong \overline{PQ}$ | $\overline{BC} \cong \overline{QR}$ |
| Ángulos correspondientes | $\sphericalangle \alpha \cong \sphericalangle \delta$ | $\sphericalangle \beta \cong \sphericalangle \varepsilon$ | $\sphericalangle \gamma \cong \sphericalangle \zeta$ |
| Lados correspondientes | $\overline{AB} \cong \overline{PQ}$ | $\overline{BC} \cong \overline{QR}$ | ${\overline{AC} \cong \overline{PR}}$ |

Ahora se presenta un recurso GeoGebra que incluye dos triángulos con dos lados homólogos congruentes y un ángulo homólogo congruente no comprendido entre éstos; es decir, no se cumplen los supuestos del criterio de congruencia de triángulos LAL, interactúa con éste para que explores el comportamiento de sus partes homólogas y concluyas la congruencia o no de ambos triángulos.
Con base en la interacción del recurso y las regularidades que identificaste sobre $\bigtriangleup BCD$ y $\bigtriangleup ABC$, contesta la pregunta ¿$\bigtriangleup ABC \cong \bigtriangleup BCD$?, (sí o no) la respuesta escríbela en el recuadro.
Al considerar que los supuestos de la congruencia de triángulos LAL no se cumplen, se llega a la conclusión de que los triángulos no son congruentes. Para que lo sean, el ángulo congruente debe estar incluido entre los dos lados congruentes en cada triángulo.

En este criterio se presenta un recurso GeoGebra que incluye dos triángulos que tienen dos ángulos y el lado adyacente a éstos congruente. Mediante tu exploración con éste descubrirás regularidades que presentan sus partes homólogas para que formules el criterio de congruencia de triángulos ALA.
Con base en la exploración del recurso y las regularidades que identificaste en la sobreposición del $\bigtriangleup PQR$ sobre el $\bigtriangleup ABC$, contesta la pregunta ¿$\bigtriangleup ABC \cong \bigtriangleup PQR$?, (sí o no) la respuesta escríbela en el recuadro.
Con base en los supuestos de que dos triángulos tienen dos ángulos y el lado adyacente (lado comprendido entre ambos ángulos), respectivamente congruentes, se establece la formulación del criterio de congruencia de triángulos ALA.
Formulación del criterio de la congruencia de triángulos ALA
Si dos ángulos y el lado incluido de un triángulo son congruentes con dos ángulos y el lado incluido de otro triángulo, entonces los triángulos son congruentes.
Demostración empírica del criterio de congruencia de triángulos ALA
Como los triángulos $\bigtriangleup ABC$ y $\bigtriangleup PQR$ coinciden en todos sus puntos, se concluye que son triángulos congruentes y que sus partes correspondientes también los son, es decir, sus ángulos correspondientes tienen la misma medida y sus lados correspondientes la misma longitud.
Con base en que $\bigtriangleup ABC \cong \bigtriangleup PQR$ arrastra a la tabla la congruencia de las partes correspondientes faltantes.
| Ángulos correspondientes | $\sphericalangle \beta \cong \sphericalangle \zeta$ | $\sphericalangle \gamma \cong \sphericalangle \delta$ | |
| Lados correspondientes | $\overline{AB} \cong \overline{PQ}$ | $\overline{BC} \cong \overline{QR}$ |
| Ángulos correspondientes | ${\sphericalangle \alpha \cong \sphericalangle \varepsilon}$ | $\sphericalangle \beta \cong \sphericalangle \zeta$ | $\sphericalangle \gamma \cong \sphericalangle \delta$ |
| Lados correspondientes | $\overline{AB} \cong \overline{PQ}$ | $\overline{BC} \cong \overline{QR}$ | ${\overline{AC} \cong \overline{PR}}$ |

Ahora se presenta un recurso GeoGebra que incluye dos triángulos con dos lados homólogos congruentes y un ángulo homólogo congruente no comprendido entre éstos; es decir, no se cumplen los supuestos del criterio de congruencia de triángulos ALA, interactúa con éste para que explores el comportamiento de sus partes homólogas y concluyas la congruencia o no de ambos triángulos.
Con base en la interacción del recurso y las regularidades que identificaste sobre $\bigtriangleup BCD$ y $\bigtriangleup ABC$, contesta la pregunta ¿$\bigtriangleup ABC \cong \bigtriangleup BCD$?, (sí o no) la respuesta escríbela en el recuadro.
Al considerar que los supuestos de la congruencia de triángulos ALA no se cumplen se llega a la conclusión que los triángulos no son congruentes, para que lo sean el ángulo congruente debe estar incluido entre los dos lados congruentes en cada triángulo.

En este criterio se presenta un recurso GeoGebra que incluye a dos triángulos que tienen respectivamente congruentes sus lados homólogos, interactúa con éste para que explores las regularidades que se presentan sus partes homólogas, lo que te permitirá la formulación del criterio de congruencia de triángulos LLL.
Con base en la exploración del recurso y las regularidades que identificaste en la sobreposición del $\bigtriangleup DEF$ sobre el $\bigtriangleup ABC$, contesta la pregunta ¿$\bigtriangleup ABC \cong \bigtriangleup DEF$?, (sí o no) la respuesta escríbela en el recuadro
Con base en los supuestos de que dos triángulos tienen respectivamente congruentes sus lados, se formula el criterio de congruencia de triángulos LLL.
Formulación del criterio de congruencia de triángulos LLL
Si los lados de un triángulo son congruentes con los lados de otro triángulo, entonces los triángulos son congruentes.
Demostración empírica del criterio de congruencia de triángulos LLL
Como los triángulos $\bigtriangleup ABC$ y $\bigtriangleup DEF$ coinciden en todas sus partes, se concluye que son triángulos congruentes y que sus partes correspondientes también los son, es decir, sus ángulos correspondientes tienen la misma medida y sus lados la misma longitud, tal como pudiste constatarlo al hacer clic en la casilla "Tesis triángulos congruentes".
Considera que $\bigtriangleup ABC \cong \bigtriangleup DEF$ y arrastra a la tabla la congruencia de las partes correspondientes.
| Ángulos correspondientes | $\sphericalangle \beta \cong \sphericalangle \delta$ | $\sphericalangle \gamma \cong \sphericalangle \zeta$ | |
| Lados correspondientes | $\overline{BC} \cong \overline{EF}$ |
| Ángulos correspondientes | ${\sphericalangle \alpha \cong \sphericalangle \varepsilon}$ | $\sphericalangle \beta \cong \sphericalangle \delta$ | $\sphericalangle \gamma \cong \sphericalangle \zeta$ |
| Lados correspondientes | ${\overline{AB} \cong \overline{DE}}$ | ${\overline{BC} \cong \overline{EF}}$ | ${\overline{AC} \cong \overline{DF}}$ |
Observa los siguientes esquemas. Después arrastra a la tabla el criterio de congruencia de triángulos con base en la congruencia de sus partes homólogas.
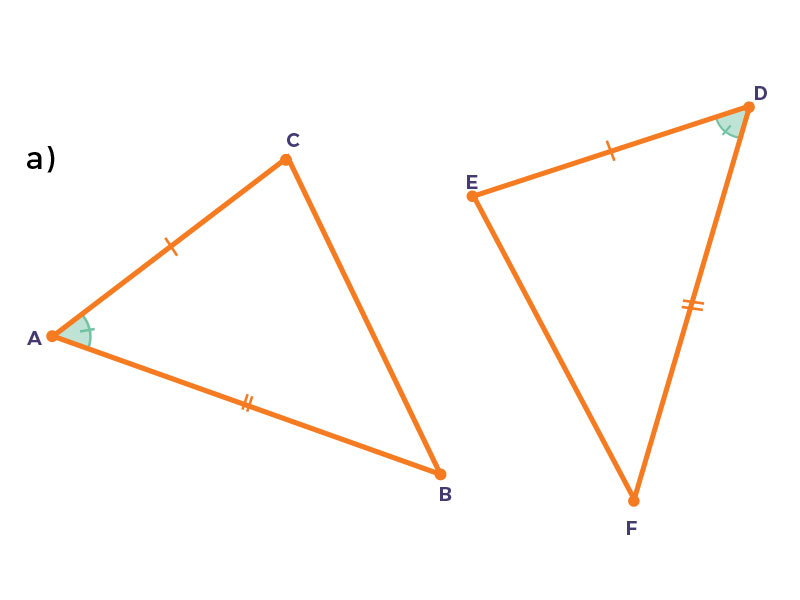
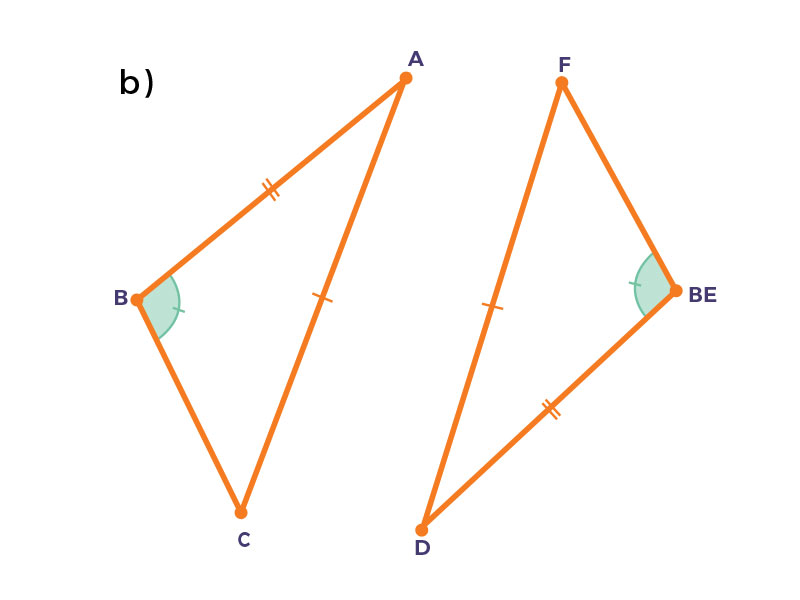
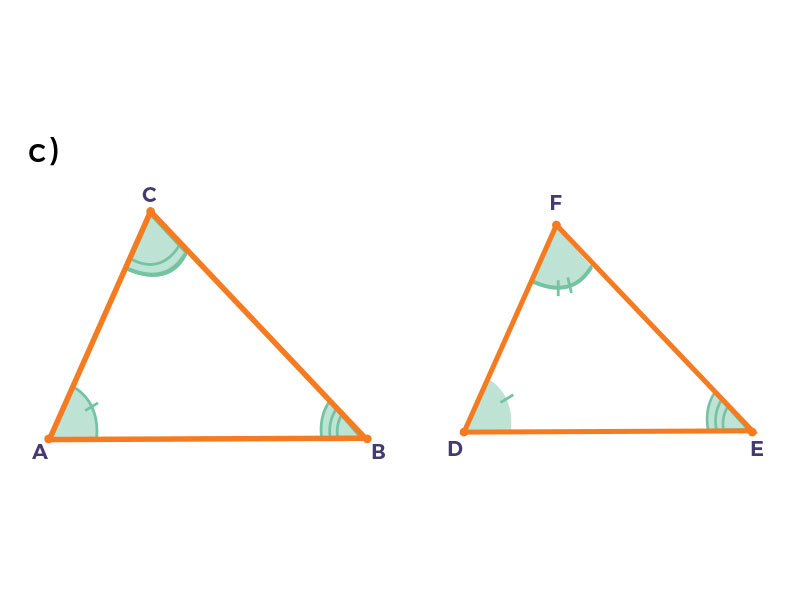
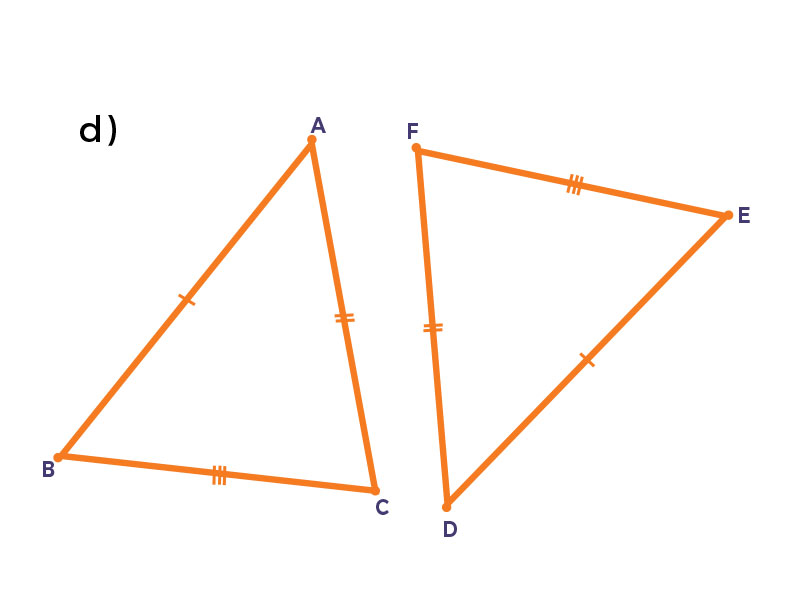
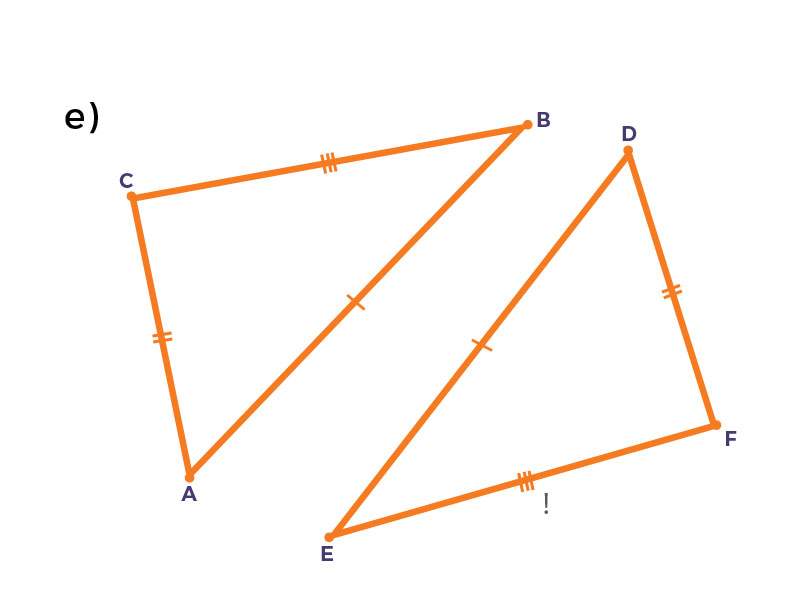
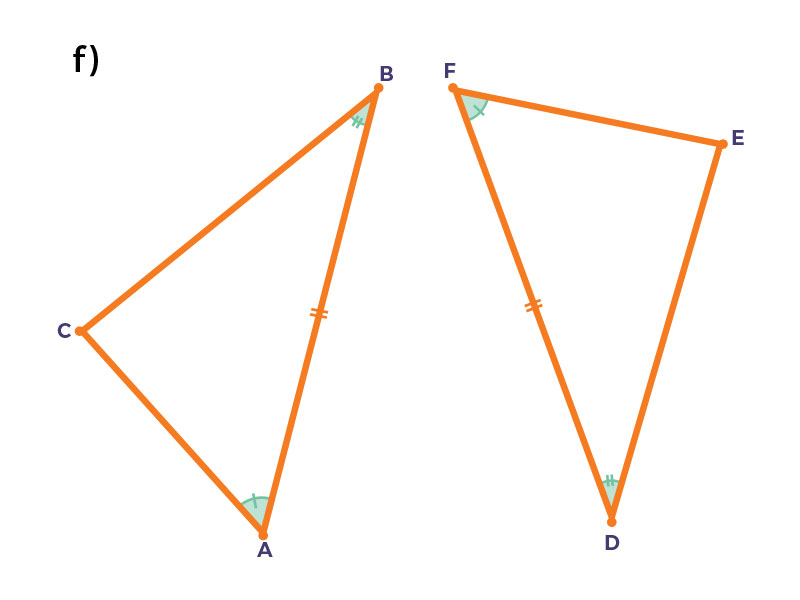
| a) | d) | e) | f) |
| a) | d) | e) | f) |
| $LAL$ | $LLL$ | $LLL$ | $ALA$ |


