En este apartado los alumnos pasan de la argumentación empírica a la argumentación formal, mediante la demostración de los procedimientos geométricos utilizados para la construcción de la mediatriz de un segmento, la bisectriz de un ángulo y el teorema del ángulo central.
La argumentación formal en la demostración de un teorema consiste en una cadena de razonamientos lógicos verdaderos para comprobar su validez y están sustentados por los elementos básicos de la geometría deductiva: definiciones, postulados, axiomas o teoremas ya demostrados.
Los teoremas demostrados se utilizan para la demostración de otros teoremas, dando como resultado la geometría deductiva o euclidiana.
| Elementos básicos | Descripción |
Definiciones |
Son los enunciados para la descripción de objetos geométricos. |
Axioma |
Es una proposición que no requiere demostración y es común para todas las ramas de las matemáticas. |
Postulado |
Es una proposición que no requiere demostración y se utiliza en la geometría. |
Teorema |
Es una proposición que requiere de una demostración, ésta consiste de una cadena de razonamientos lógicos verdaderos y cada uno de ellos está fundamentado por definiciones, axiomas, postulados o teoremas ya demostrados. |
- Un segmento es una porción de una recta y está limitado en sus extremos por un punto.
- Ángulos adyacentes son aquellos que tienen el mismo vértice y un lado en común.
- Dos rectas son paralelas cuando estando en el mismo plano y prolongadas al infinito no se cortan.
- Dos rectas son perpendiculares cuando convergen para formar ángulos adyacentes congruentes.
- Triángulo es la figura geométrica limitada por tres rectas que se cortan dos a dos, los puntos de intersección son los vértices del triángulo.
- Figuras congruentes son aquellas que al sobreponerlas coinciden en todos sus partes, es decir, cuando tiene la misma forma y el mismo tamaño.
- Dos triángulos son congruentes cuando tienen congruentes sus partes correspondientes.
- Bisectriz de un ángulo. Es la recta que divide a un ángulo en dos ángulos congruentes.
- Mediatriz de un segmento. Es la recta perpendicular al segmento y lo divide en partes congruentes. El punto de intersección es el punto medio del segmento.
- El todo es mayor que la parte.
- Dos cantidades iguales a una tercera son iguales entre sí, es decir, si a=b y b=c, se concluye que a=c. A este axioma también se le conoce como la ley de transitividad.
- Toda cantidad se puede reemplazar por su igual.
- Si a cantidades iguales se les suma, resta, multiplica o divide por otras también iguales, los resultados son iguales. Cabe mencionar que en la división el divisor debe ser diferente de cero.
- El todo es igual a la suma de sus partes.
- Dos puntos determinan una línea y solo una.
- Todo segmento se puede prolongar en ambas direcciones.
- Siempre es posible construir una circunferencia de centro y radio dados.
- Toda figura puede cambiar de posición sin alterar su forma y dimensiones.
- Toda figura geométrica es congruente a sí misma.
- Dos rectas no pueden cortarse en más de un punto.
- Todos los ángulos rectos son iguales.
- Por un punto exterior a una recta solo puede trazarse una sola recta paralela a la dada.
- Por un punto exterior a una recta solo puede trazarse una sola recta perpendicular a la dada.
Hipótesis
Son los supuestos que se especifican en un teorema.
Tesis
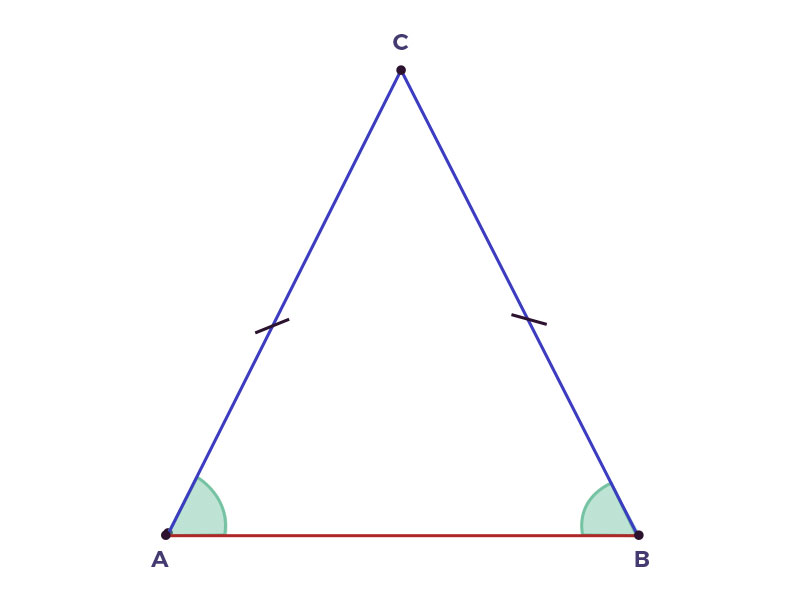
Es lo que se quiere demostrar en un teorema. Por ejemplo, en el teorema. En todo triángulo isósceles, los ángulos opuestos a los lados congruentes son congruentes. La hipótesis supone que el triángulo es isósceles y que los lados $\overline{AC}$ y $\overline{BC}$ son congruentes, mientras que la tesis consiste en demostrar la congruencia de los ángulos ${\color{Blue}\sphericalangle A \cong \sphericalangle B}$.
Teorema
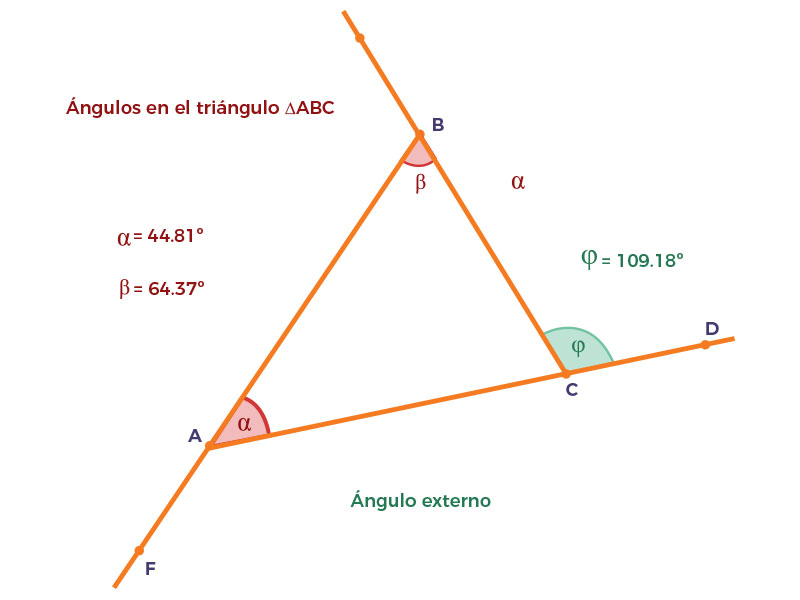
En todo triángulo un ángulo exterior es igual a la suma de los dos ángulos interiores opuestos no adyacentes.
Hipotesis
En el ${\color{Blue}\bigtriangleup ABC}$, ${\color{Blue}\sphericalangle \varphi}$ es un ángulo exterior.
Tesis
${\color{Blue}\sphericalangle \varphi = \sphericalangle \alpha + \sphericalangle \beta}$
Demostración de la construcción de la mediatriz de un segmento
Para facilitar tu comprensión de la demostración de los procedimientos geométricos para las construcciones mencionadas, se presenta la demostración de la construcción de la recta mediatriz al segmento $\overline {AB}$. Con base en ésta se plantearán actividades en las demostraciones de las construcciones restantes.
En la tabla se presenta la construcción de la recta mediatriz al segmento $\overline {AB}$ así como, la descripción de la construcción, la hipótesis y la tesis.
Construcción de la mediatriz a $\overline {AB}$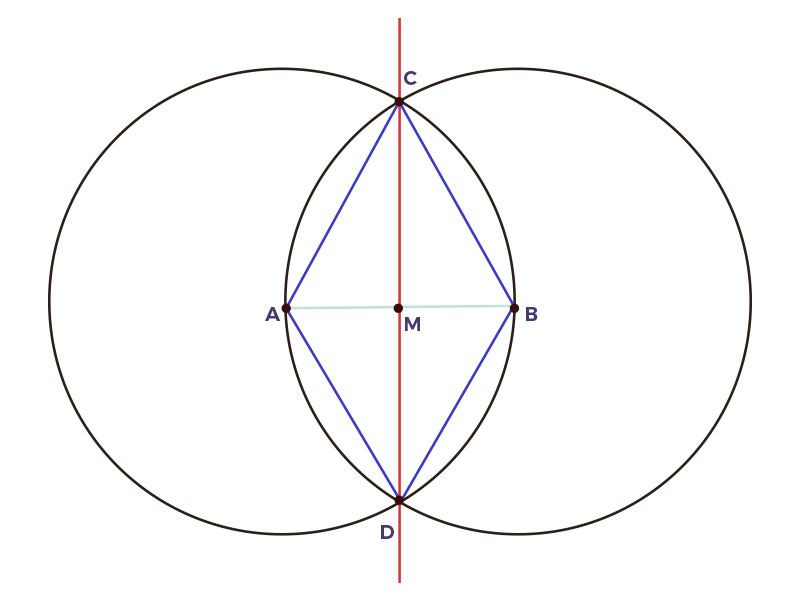 
Hipótesis: Sea $\overline {AB}$el segmento dado Tesis: $\overline{AM} \cong \overline{MB}$ y $\overleftrightarrow {CD} \bot \overline{AB}$ |
Descripción de la construcción de la mediatriz:
|
La demostración de la construcción de la recta mediatriz al segmento $\overline {AB}$ se presenta en la tabla, así como, las proposiciones y razones para su fundamentación.
| Proposiciones | Razones |
1. $\overline{AC} \cong \overline{BC}$ y $\overline{AD} \cong \overline{BD}$ |
Por construcción son radios de las circunferencias con centro en $A$ y $B$. |
2. $\overline{CD} \cong \overline{CD}$ |
Postulado. Toda figura geométrica es congruente así misma. |
3. $\bigtriangleup ACD \cong \bigtriangleup CBD$ |
Criterio de congruencia de triángulos $LLL$ (pasos 1 y 2). |
4. $\sphericalangle ACM \cong \sphericalangle BCM$ |
Definición congruencia de triángulos. Las partes correspondientes de triángulos congruentes son congruentes (paso 3). |
5. $\overline{CM} \cong \overline{CM}$ |
Postulado. Toda figura geométrica es congruente a sí misma. |
6. $\bigtriangleup ACM \cong \bigtriangleup BCM$ |
Criterio de congruencia de triángulos LAL (pasos 1, 4 y 5). |
7. $\overline{AM} \cong \overline{BM}$ |
Definición congruencia de triángulos. Las partes correspondientes de triángulos congruentes son congruentes (paso 6). |
8. $\sphericalangle AMC \cong \sphericalangle CMB$ |
Definición congruencia de triángulos. Las partes correspondientes de triángulos congruentes son congruentes (paso 6). |
9. $\overleftrightarrow {CD} \bot \overline{AB}$ |
Definición de rectas perpendiculares. Dos rectas son perpendiculares cuando convergen para formar ángulos adyacentes congruentes (paso 8). |
La cadena de razonamientos lógicos realizados para la demostración de la construcción de la recta mediatriz, $\overleftrightarrow{CD}$ al $\overline{AB}$, valida la construcción.
Demostración de la construcción de la bisectriz de un ángulo
En la siguiente tabla se te presentan la construcción y la descripción de la recta bisectriz del ángulo $\sphericalangle A$, así como, algunas proposiciones y razones para su demostración.
Construcción de la recta bisectriz del $\sphericalangle BAC$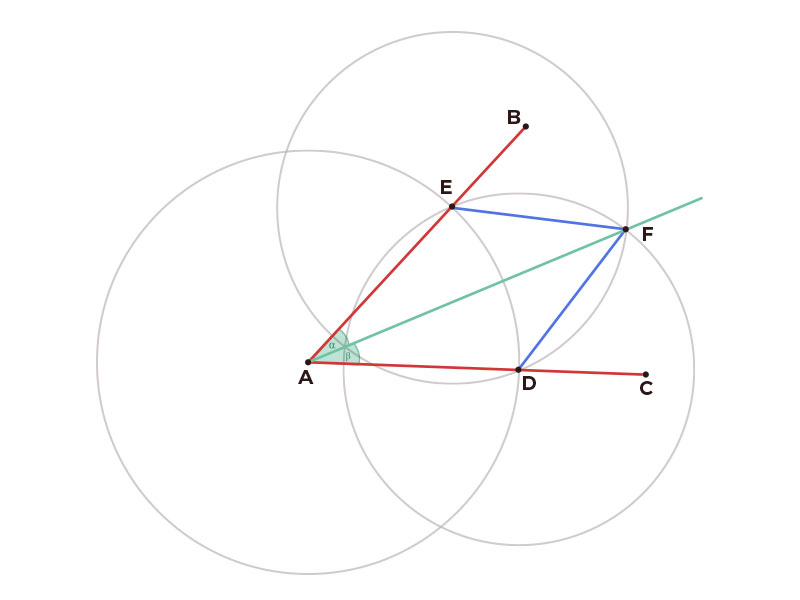 
Hipótesis: Sea $\measuredangle BAC$ el ángulo dado Tesis: $\sphericalangle \alpha \cong \sphericalangle \beta$ |
Descripción de la construcción de la bisectriz:
|
Demostración de la construcción de la bisectriz del $\sphericalangle BAC$
| Proposiciones | Razones |
| 1. $ \overline{AD} \cong \overline{AE}$ | Por construcción los segmentos $\overline{AD}$ y $\overline{AE}$ son radios de la circunferencia que pasa por los puntos $D$ y $E$ |
| 2. | Por construcción los segmentos $\overline{EF}$ y $\overline{DF}$ son radios de las circunferencias con centro en los puntos $E$ y $D$, ambas con radio la longitud del $\overline{DE}$. |
| 3. | Postulado. Toda figura geométrica es congruente a sí misma. |
| 4. | Criterio de congruencia de triángulos LLL. |
| 5. | Las partes correspondientes de triángulos congruentes son congruentes. |
| 6. La recta $\overline{AF}$ es bisectriz del ángulo $\sphericalangle BAC$ | Definición de la recta bisectriz. Es la recta que divide a un ángulo en dos ángulos congruentes. |
| Proposiciones | Razones |
| 1. $ \overline{AD} \cong \overline{AE}$ | Por construcción los segmentos $\overline{AD}$ y $\overline{AE}$ son radios de la circunferencia que pasa por los puntos $D$ y $E$ |
| 2. $\overline{EF} \cong \overline{DF}$ | Por construcción los segmentos $\overline{EF}$ y $\overline{DF}$ son radios de las circunferencias con centro en los puntos $E$ y $D$, ambas con radio la longitud del $\overline{DE}$. |
| 3. $\overline{AF} \cong \overline{AF}$ | Postulado. Toda figura geométrica es congruente a sí misma. |
| 4. $\bigtriangleup ADF \cong \bigtriangleup AEF$ | Criterio de congruencia de triángulos LLL. |
| 5. $\sphericalangle \alpha \cong \sphericalangle \beta$ | Las partes correspondientes de triángulos congruentes son congruentes. |
| 6. La recta $\overline{AF}$ es bisectriz del ángulo $\sphericalangle BAC$ | Definición de la recta bisectriz. Es la recta que divide a un ángulo en dos ángulos congruentes. |
Demostración del teorema del ángulo central
En la siguiente tabla se te presentan la construcción del ángulo central y un ángulo inscrito para la formulación del teorema del ángulo central. El ángulo inscrito $\beta$ es la mitad de la medida del ángulo central $\alpha$. Para la demostración escribe en la tabla las proposiciones y/o razones según corresponda.
Construcción de los ángulos inscrito y central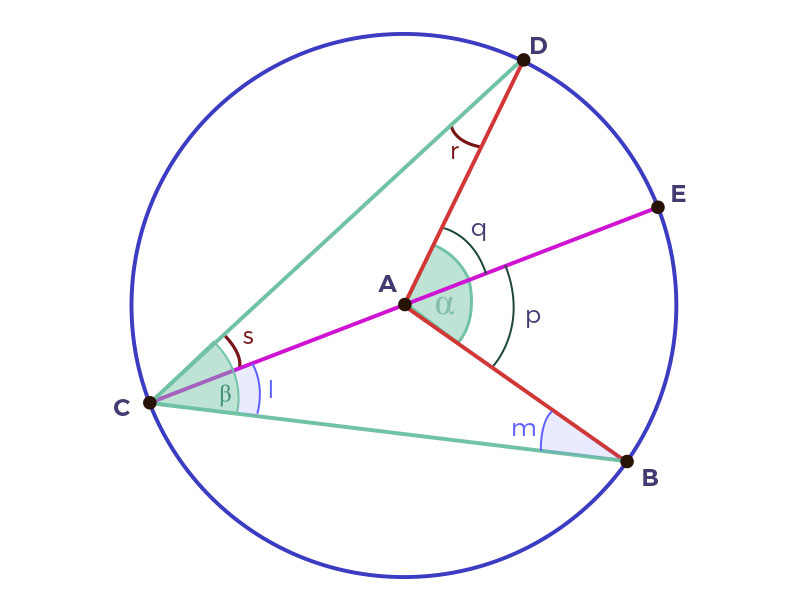 
Hipótesis: $\sphericalangle \alpha$ es ángulo central y $\sphericalangle \beta$ es ángulo inscrito de la circunferencia. Tesis: $\sphericalangle \beta = \tfrac{1}{2} \sphericalangle \alpha$ |
Descripción de la construcción de los ángulos central e inscrito y la formulación del teorema del ángulo central:
Teorema del ángulo central. La medida del ángulo inscrito en una circunferencia es la mitad del ángulo central. |
Demostración del teorema del ángulo central
| Proposiciones | Razones |
| 1. | Teorema del ángulo externo en un triángulo. El $\sphericalangle p$ es ángulo externo del triángulo isósceles $\bigtriangleup ABC$. |
| 2. $\sphericalangle l \cong \sphericalangle m$ | Teorema. En todo triángulo isósceles, los ángulos opuestos a los lados congruentes son congruentes. |
| 3. | Axioma. Toda cantidad se puede sustituir por su igual (pasos 1 y 2). |
| 4. $\sphericalangle q = \sphericalangle s + \sphericalangle r$ | Teorema del ángulo externo en un triángulo. El $\sphericalangle q$ es ángulo externo del triángulo isósceles $\bigtriangleup ACD$. |
| 5. $\sphericalangle s = \sphericalangle r$ | Teorema. En todo triángulo isósceles, los ángulos opuestos a los lados congruentes son congruentes. |
| 6. | Axioma. Toda cantidad se puede sustituir por su igual (pasos 4 y 5). |
| 7. $\sphericalangle p + \sphericalangle q = 2 \sphericalangle l + 2 \sphericalangle s = 2 ( \sphericalangle l + \sphericalangle s )$ | Axioma. Si a cantidades iguales se les suma otras también iguales, los resultados son iguales (pasos 3 y 6). |
| 8. | Axioma. El todo es la suma de sus partes (paso 7). |
| 9. $\sphericalangle \beta = \tfrac{1}{2} ( \sphericalangle \alpha )$ | Axioma. Toda cantidad se puede reemplazar por su igual |
| Proposiciones | Razones |
| 1. $\sphericalangle p = \sphericalangle l + \sphericalangle m$ |
Teorema del ángulo externo en un triángulo. El $\sphericalangle p$ es ángulo externo del triángulo isósceles $\bigtriangleup ABC$. |
2. $\sphericalangle l \cong \sphericalangle m$ |
Teorema. En todo triángulo isósceles, los ángulos opuestos a los lados congruentes son congruentes. |
3. $\sphericalangle p = \sphericalangle l + \sphericalangle l = 2 \sphericalangle l$ |
Axioma. Toda cantidad se puede sustituir por su igual (pasos 1 y 2). |
4. $\sphericalangle q = \sphericalangle s + \sphericalangle r$ |
Teorema del ángulo externo en un triángulo. El $\sphericalangle q$ es ángulo externo del triángulo isósceles $\bigtriangleup ACD$. |
| 5. $\sphericalangle s = \sphericalangle r$ |
Teorema. En todo triángulo isósceles, los ángulos opuestos a los lados congruentes son congruentes. |
| 6. $\sphericalangle q = \sphericalangle s + \sphericalangle r = 2 \sphericalangle s$ |
Axioma. Toda cantidad se puede sustituir por su igual (pasos 4 y 5). |
| 7. $\sphericalangle p + \sphericalangle q = 2 \sphericalangle l + 2 \sphericalangle s = 2 ( \sphericalangle l + \sphericalangle s )$ |
Axioma. Si a cantidades iguales se les suma otras también iguales, los resultados son iguales (pasos 3 y 6). |
| 8. $\sphericalangle \alpha = 2 ( \sphericalangle \beta )$ |
Axioma. El todo es la suma de sus partes (paso 7). |
9. $\sphericalangle \beta = \tfrac{1}{2} ( \sphericalangle \alpha )$ |
Axioma. Toda cantidad se puede reemplazar por su igual |