Problemas de aplicación

Semicírculo

Escribir

Determina el perímetro $P$ y el área $A$ del siguiente semicírculo de radio igual a 2 metros.

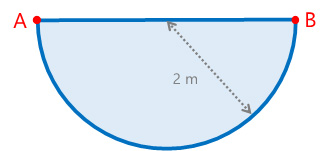
Círculo y circunferencia

Definiciones, sea:

  • El ángulo que está sin rellenar es de 90° (que corresponde a una cuarta parte de la circunferencia y del círculo) por lo que el perímetro y el área corresponderá a ¾ de la figura completa.

Perímetro buscado:

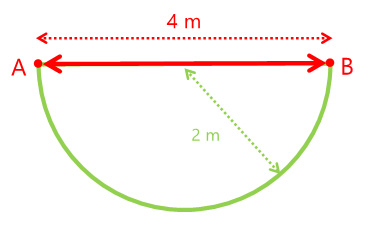
El perímetro de la semicircunferencia es la suma de la longitud del arco ${\color{green} {\stackrel{\textstyle\frown}{\mathrm{AB}}}}$ y el segmento ${ \color{red} {\overline{AB}} }$, es decir: $P = { \color{red} {\overline{AB}} } + {\color{green} {\stackrel{\textstyle\frown}{\mathrm{AB}}}}$

Círculo y circunferencia
Segmento ${ \color{red} {\overline{AB}} }$: 4 m.
Arco ${\color{green} {\stackrel{\textstyle\frown}{\mathrm{AB}}}}$ semicírculo: ${ \color{red} {+} } {(\tfrac{1}{2})2 \pi r = \pi (2)} =$ 2 $\pi$ m.
Perímetro total: $= 4 + 2\pi$ m.
$=$ 10.28 m.
Es necesario que escribas las respuestas para recibir retroalimentación.

Área buscada:

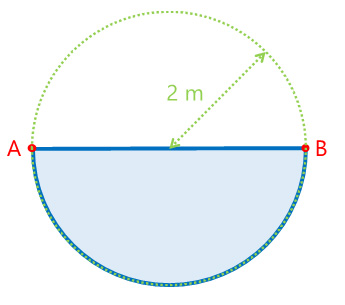
El área del semicírculo $A_s$ es la mitad del área total del círculo $A_c$ de radio $r$, es decir: $A_s = \tfrac{1}{2}A_c = \tfrac{1}{2} \pi r^2$

Círculo y circunferencia
Área del semicírculo $( \tfrac {1}{2} ) \pi r^2 = ( \tfrac {1}{2} ) \pi(2)^2 =$ 2 $\pi$ m$^2$.
Área: $=$ 6.28 m$^2$.

   Regresa al principio del fichero para resolver el problema 2   

Jardinera

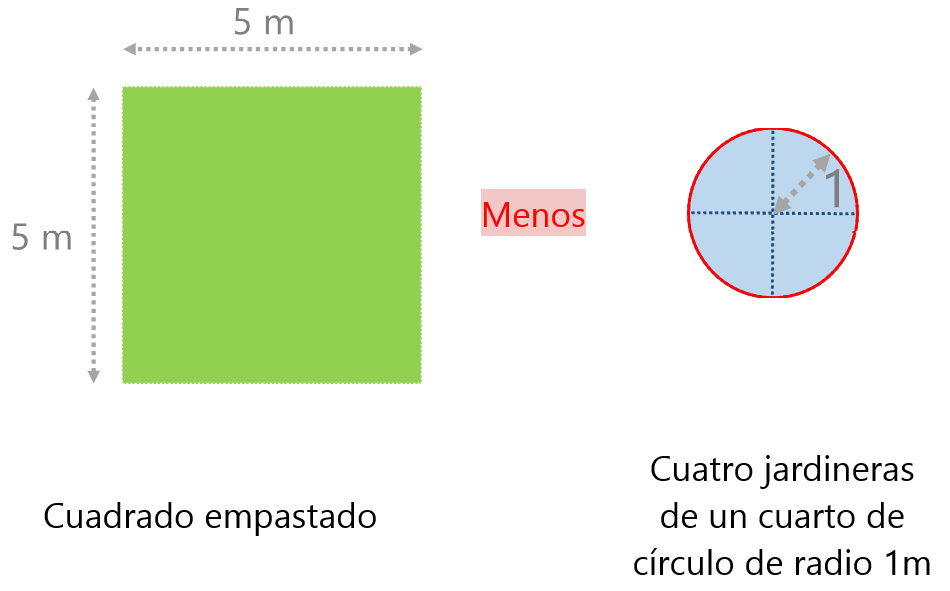
En las esquinas de un pequeño patio cuadrado de 5m de lado se han colocado cuatro jardineras; las formas de las jardineras corresponden a cuartos de circunferencia, cuyos radios $r$ miden 1m de largo.

Escribir

Determina la magnitud del área empastada (área sombreada).

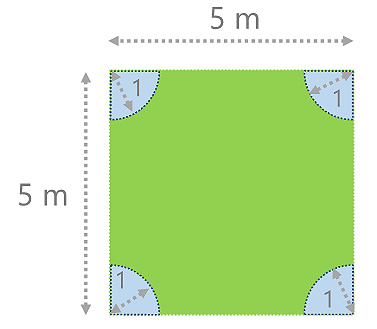
Círculo y circunferencia

Definiciones, sea:

  • El ángulo que está sin rellenar es de 90° (que corresponde a una cuarta parte de la circunferencia y del círculo) por lo que el perímetro y el área corresponderá a ¾ de la figura completa.

Área buscada:

El área total del jardín $A_t$ se obtiene mediante la fórmula para el área del cuadrado, es y restando las cuatro esquinas de las jardineras:

Círculo y circunferencia
Área del cuadrado $=l^2=($ 5$) ($ 5$)=25$ m$^2$.
Menos un círculo: ${ \color{red} {-} } {4( \tfrac {1}{4} ) \pi r^2 = \pi r^2 = \pi(1)^2 =}$ 1 $\pi$ m$^2$.
Área: $= 25 - \pi$ m$^2$.
$=$ 21.86 m$^2$.

   Regresa al principio del fichero para resolver el problema 3   

Pared de madera

Escribir

Completa la información respecto al área de la construcción de madera.

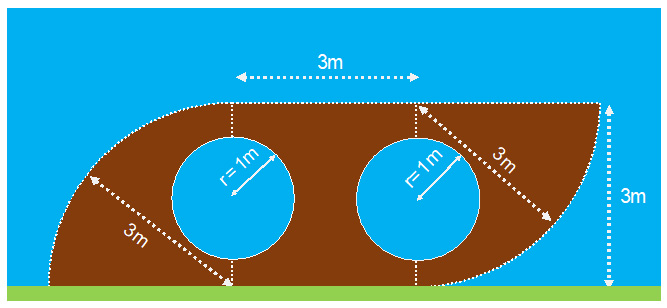
Una compañía quiere colocar una pared con su logotipo en medio del jardín de la entrada principal de sus oficinas. La construcción de madera tiene las siguientes dimensiones:

Círculo y circunferencia

Consideraciones:

Hay que notar que existen dos círculos huecos en el en centro ¿Cuál es el área que ocupará la parte frontal de la estructura?

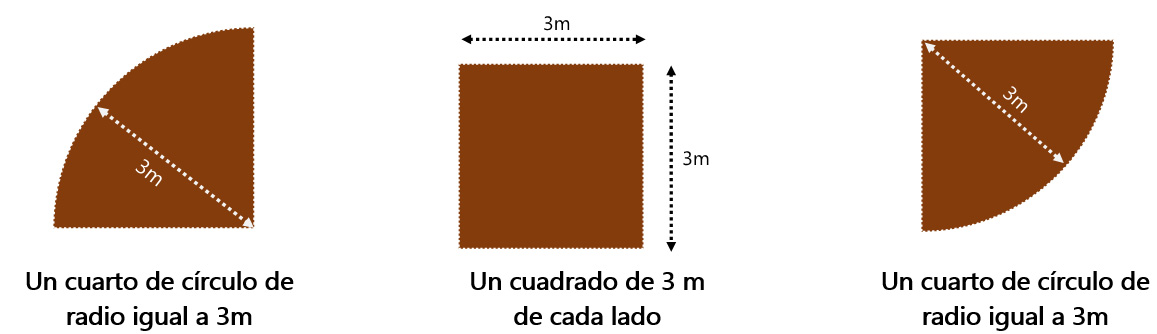
Círculo y circunferencia

Las dos áreas que se restarán son las “ventanas” circulares en medio de la estructura, con radio igual a 1 m:

Círculo y circunferencia

Cálculo del área:

Dos cuartos de círculo de radio igual a 3 metros $2 ( \tfrac {1}{2} ) \pi r^2 = \tfrac {1}{2} \pi($ 3$)^2 = 4.5\pi$ m$^2$
Un cuadrado de 3 metros de lado ${ \color{red} {+} } {l^2 = (3)^2 = 9 m^2}$
Dos círculos de 1 metro de radio ${ \color{red} {-} } {2\pi r^2 = 2\pi(}$ 1 $)^2 = 2\pi$ m$^2$
Área: $= 4.5\pi + 9 - 2\pi = 2.5\pi + 9$m$^2$
$=$ 16.85 m$^2$.

   Regresa al principio del fichero para resolver el problema 4   

Letra C

Un diseñador gráfico desea construir la siguiente letra a partir de los datos que proporciona en su diseño.

Escribir

Determina el área y el perímetro de la región sombreada en la siguiente figura.

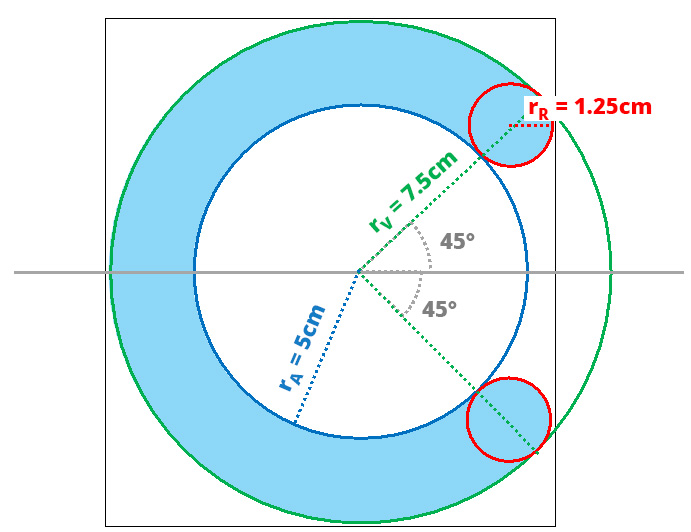
Círculo y circunferencia

Definiciones, sea:

  • El ángulo que está sin rellenar es de 90° (que corresponde a una cuarta parte de la circunferencia y del círculo) por lo que el perímetro y el área corresponderá a ¾ de la figura completa.

Perímetro buscado:

¾ de la circunferencia exterior: $( \tfrac {3}{4} ) 2 \pi r = 1.5 \pi ($ 7.5$) = 11.25 \pi$ cm
¾ de la circunferencia interior: ${ \color{red} {+} } {( \tfrac {3}{4} ) 2 \pi r = 1.5 \pi (5) =}$ 7.5 $\pi$ cm
2 semicircunferencias con diámetro=2.5 ${ \color{red} {+} } {2( \tfrac {1}{2} ) \pi d = \pi (2.5) = 2.5\pi}$ cm
Perímetro total: $=11.25 \pi + 7.5 \pi +$ 2.5$\pi$
$=21.25\pi$ cm
$=$ 66.76cm

Área buscada:

¾ del área del exterior $( \tfrac {3}{4} ) \pi r^2 = ( \tfrac {3}{4} ) \pi($ 7.5 $)^2 = 42.1875 \pi$ cm$^2$
Menos ¾ del área del interior ${ \color{red} {-} } {( \tfrac {3}{4} ) \pi r^2 = ( \tfrac {3}{4} ) \pi(}$ 5 $)^2 = 18.75 \pi$ cm$^2$
Mas dos semicircunferencias, que hacen una circunferencia de radio 1.25 ${ \color{red} {+} } {( \tfrac {3}{4} ) \pi r^2 = ( \tfrac {3}{4} ) \pi(}$ 1.25 $)^2 = 1.5625 \pi$ cm$^2$
Área total: $= 42.1875 \pi - 18.75 \pi + 1.5625 \pi$ cm$^2$
$= 25\pi$ cm$^2$
$=$ 78.54 cm$^2$

   Fin de problemas de aplicación