Dado un círculo de radio $r$ y diámetro $d$, la longitud de la circunferencia está dada por la fórmula $C = \pi d = 2 \pi r$.
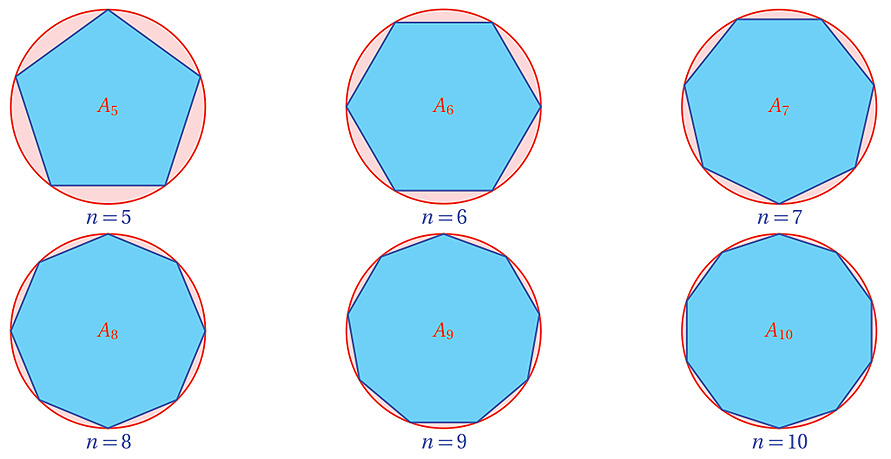
En la figura se observa que conforme aumenta el número de lados del polígono, el área del polígono se aproxima al área del círculo. En consecuencia, el área del círculo $A_c$ es igual al área del polígono $A_p$ cuando el número de lados de éste es muy grande; es decir: $$A_c = A_p$$
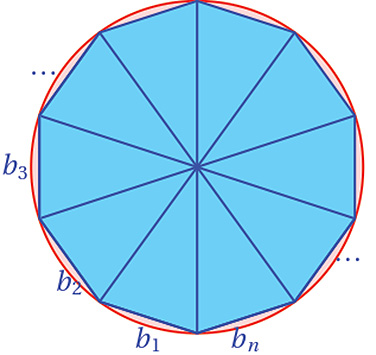
Para calcular el área del polígono de $n$ lados, se divide al polígono en $n$ triángulos, cuyas bases sean los lados del polígono y que hagan vértice en el centro de la circunferencia, como se muestra en la figura. El área del polígono es igual a la suma de las áreas de todos los triángulos.
Cuando el número de lados del polígono es sumamente grande, se tiene que la altura de los triángulos es praticamente igual a la longitud del radio $r$ de la circunferencia, y que la suma de las longitudes $b_i$ de las bases de todos los triangulos es casi igual a la longitud $C$ de la circunferencia.
Demostración
| Es decir: | $C=b_1+b_2+b_3+... +b_n$ |
| Y como $C=2 \pi r$, entonces | $b_1+b_2+b_3+... +b_n = 2 \pi r$ |
| Además, el área de cada uno de los triángulos $A_t$ está dada por la expresión: | $$A_t = b \frac{r}{2}$$ Dónde:
|
| Como el área del polígono está dada por la suma de las áreas de todos los triágulos, se tiene: | $A_p = b_1 \frac{r}{2} +b_2 \frac{r}{2} + b_3 \frac{r}{2} +... +b_n \frac{r}{2} = 2 \pi r$ |
| Dado que $\frac{r}{2}$ es un factor común en todos los elementos de la derecha, la expresión anterior puede simplificarse como: | $A_p = (b_1 +b_2 + b_3 +... +b_n) \frac{r}{2} = 2 \pi r$ |
| Utilizando la expresión (3), la última expresión obtenida se puede reescribir como: | $$A_p = (2 \pi r) \frac{r}{2} = 2 \pi r$$ $$A_p = \pi r^2$$ |
| Por lo tanto: | $$A_c = \pi r^2$$ |
Teorema
Dado un circulo de radio $r$, el área está dada por la fórmula $A=\pi r^2$
El área de un círculo se puede calcular a partir del área de un polígono regular inscrito de n lados; conforme el número de lados del polígono es mayor, el área de éste se aproxima al área del círculo.
- Se crearán polígonos regulares de $n$ lados circunscritos en un círculo, las esquinas de los polígonos coincidirán con la circunferencia.
- Se calculará el área de los triángulos rectángulos como se muestran en la figura. La apotema ($a$) parte del centro del círculo a cada una de las bases inscritas, en cada uno de los $n$ triángulo isósceles se tendrán dos triángulos reflejados (congruentes); nota que se forman $2$ triángulos rectángulos en cada triángulo isósceles, por lo que se tendrán $2n$ triángulos rectángulos en cada polígono de $n$ lados.
Procedimiento para el cálculo del área del triángulo rectángulo mostrado en la figura
- Se define un polígono regular de $n=4$ lados (cuadrado) inscrito en la figura:
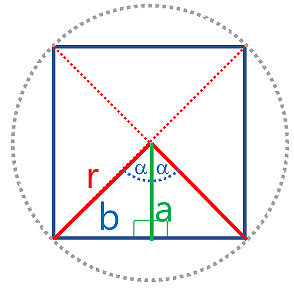
Se forman $n=4$ triángulos isósceles, conformados por dos triángulos rectángulos con hipotenusa igual a $r$, un ángulo $\alpha$ igual a la circunferencia dividida entre $n=4$ lados ($n=4$ triángulos isósceles) y, su vez, divididos entre 2:
| Por lo que el ángulo $\alpha$: | $$\alpha=\tfrac{360^o}{2n}$$ |
| El cateto adyacente al ángulo $α$ llamado apotema ($a$) y la base $b$ que corresponde al cateto adyacente. | |
| De cada triángulo rectángulo que se forma:$b$ es la base y la apotema $a$ la altura. El área de cada uno de los $2n$ triángulos es: | $$A_{TR}=\frac{ba}{2}$$ |
| Dónde, por identidades trigonométricas, respecto a $α$: | $$sen ({\alpha})=\frac{Cateto \hspace{0.25em} Opuesto}{Hipotenusa}=\frac{b}{r}$$ $$\cos({\alpha})=\frac{Cateto \hspace{0.25em} Adyacente}{Hipotenusa}=\frac{a}{r}$$ |
| Despejando la base y la apotema: | $$b=r \cdot {sen (\alpha)}$$ $$a=r \cos(\alpha)$$ |
| Obteniendo el área de al triángulo: | $$A_{TR}=\tfrac{ (r sen (\alpha)) (r \cos(\alpha))} {2}$$ $$A_{TR}=\tfrac{(sen \alpha) (\cos\alpha) r^2} {2}$$ |
| El área del triángulo isósceles: | $$A_{TI}=2A_{TR}=2\tfrac{(sen \alpha) (\cos\alpha) r^2} {2}$$ $$A_{TI}=(sen \alpha) (\cos\alpha) r^2$$ |
| El área total es igual a la suma de n triángulos isósceles: | $$A_p=n(sen \alpha) (\cos\alpha) r^2$$ Dónde: $n$ es el número de lados del polígono con el que deseamos aproximar la solución y $$\alpha=\tfrac{360^o}{2n}$$ |
| Para un cuadrado, polígono regular de $n=4$ lados: | 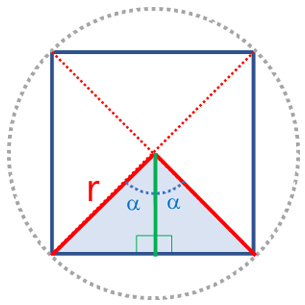 |
| El cálculo del ángulo sería: | $$\alpha=\tfrac{360^o}{2(4)}=45^o$$ |
| Por lo tanto, el área sería: | $$A_p=4(sen 45^o)(cos 45^o)r^2$$ $$A_p=4(0.7071)(0.7071)r^2$$ $$A_p=2r^2$$ |
| Para un cuadrado, polígono regular de $n=8$ lados: | 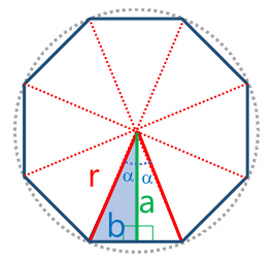 |
| El cálculo del ángulo sería: | $$\alpha=\tfrac{360^o}{2(8)}=22.5^o$$ |
| Por lo tanto, el área sería: | $$A_p=8(sen 22.5^o)(cos 22.5^o)r^2$$ $$A_p=8(0.382683)(0.923880)r^2$$ $$A_p=2.828427 r^2$$ |
Termina fichero, realiza el ejercicio
Completa la siguiente tabla utilizando la fórmula que aparece a continuación. Puedes utilizar una calculadora científica o una hoja de cálculo (el ángulo debe estar en grados, no en radianes, para utilizar la expresión con radianes recuerda que $360^o=2π)$, recuerda que: $$A= n sen(\tfrac{360^o}{2n}) \cos(\tfrac{360^o}{2n})r^2$$


