Actividad final

Rectas y segmentos

Seleccionar

Evalúa si cada afirmación es verdadera (V) o falsa (F) con respecto a la figura:

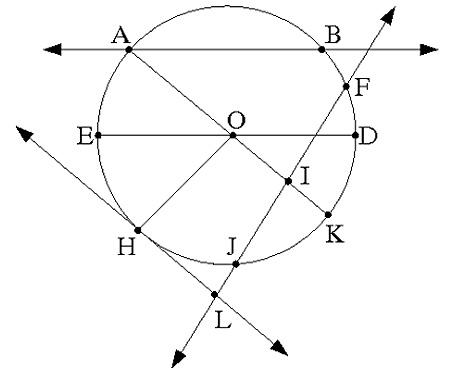
	Verdadero	Falso
1. La recta $AB$ es una cuerda de la circunferencia.
2. La recta $HL$ es secante a la circunferencia.
3. La recta $AB$ es secante a la circunferencia.
4. El arco $DE$ es el diámetro de la circunferencia.
5. El segmento $OH$ es radio de la circunferencia.

Regresa al principio del fichero para resolver la actividad 2

Triángulo inscrito

Escribir

Calcula el área del triángulo equilátero (azul) inscrito en el círculo.

Perímetro:	5.196152 $r$
Área:	1.299038 $r^2$

Regresa al principio del fichero para resolver la actividad 3

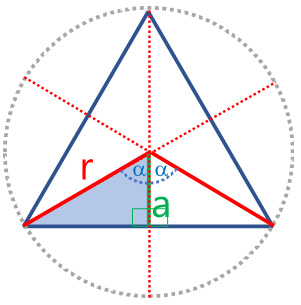
Regiones

Escribir

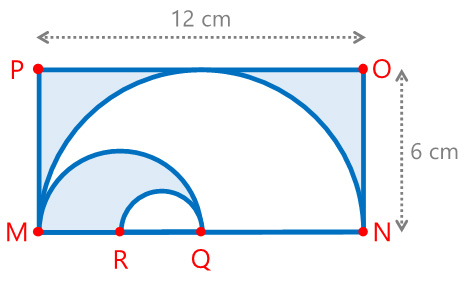
Determina el área y el perímetro de la región sombreada si $ON=6$cm, $MN=12$cm, $Q$ es el punto medio de $MN$ y $R$ es el punto medio $MQ$. Completa los cuadros de texto con los valores calculados.

Perímetro:	56.99 cm
Área:	26.05 cm$^2$

A partir de la figura, mostramos con azul oscuro el perímetro y sombreada el área a calcular.

Definiciones, sea:

$R$: rectángulo exterior, de 12 cm ancho por 6 cm de altura.
$C_1$: El semicírculo de radio 6 cm
$C_1$: El semicírculo de radio 3 cm
$C_1$: El semicírculo de radio 1.5 cm

Perímetro buscado:

Lado superior de $R$	12cm
Más dos lados a la izquierda y a la derecha de $R$	${ \color{red} {+} } {2(6) = 12}$cm
Más el perímetro del semicírculo $C_1$	${ \color{red} {+} } {\tfrac{1}{2} (2 \pi r)= \pi r = 6 \pi}$cm
Más el perímetro del semicírculo $C_2$	${ \color{red} {+} } {\tfrac{1}{2} (2 \pi r)= \pi r = 3 \pi}$cm
Más el perímetro del semicírculo $C_3$	${ \color{red} {+} } {\tfrac{1}{2} (2 \pi r)= \pi r = 1.5 \pi}$cm
Perímetro total:	$$= 12+12+6 \pi + 3 \pi + 1.5 \pi$$ $$=24+10.5 \pi$$ $$=56.99$$

Área buscada:

Área de $R$	$bh=(12)(6)=72$cm$^2$
Menos el área del semicírculo $C_1$	${ \color{red} {-} } {\tfrac{1}{2} (\pi r^2)= \tfrac{1}{2} \pi (6)^2 = 18 \pi}$cm$^2$
Menos el área del semicírculo $C_2$	${ \color{red} {+} } {\tfrac{1}{2} (\pi r^2)= \tfrac{1}{2} \pi (3)^2 = 4.5 \pi}$cm$^2$
Menos el área del semicírculo $C_3$	${ \color{red} {-} } {\tfrac{1}{2} (\pi r^2)= \tfrac{1}{2} \pi (3)^2 = 1.125 \pi}$cm$^2$
Área total:	$$= 72-18 \pi + 4.5 \pi + 1.125 \pi$$ $$=72-14.625 \pi$$ $$=26.05$$

Regresa al principio del fichero para resolver la actividad 4

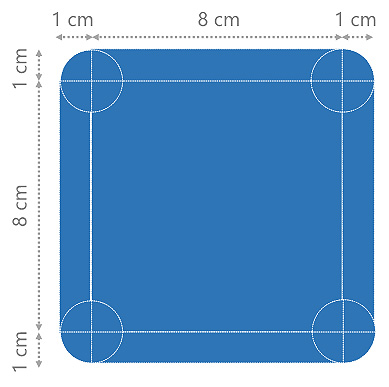
Cuadrado redondeado

Escribir

Determina el área y el perímetro de la región sombreada. Completa los cuadros de texto con los valores calculados.

Perímetro:	38.28 cm
Área:	99.14 cm$^2$

A partir de la figura se muestran figuras las distintas figuras interiores en colores distintos para distinguir rectángulos verdes, el cuadrado rojo y sectores de círculos en color azul:

Definiciones, sea:

Las cuatro esquinas redondeadas (de color azul) son un cuarto de círculo cada una, al juntarlas forman un círculo de radio $r=1$cm
Se forman cuatro rectángulos $R_1$ (de color verde) de 1 cm de ancho por 8 cm de largo.
Se forma un cuadrado $R_2$ (de color rojo) de 8 cm por cada lado.

Perímetro buscado:

Circunferencia (región azul):	$2 \pi r = 2 \pi (1) = 2 \pi$cm
Más cuatro lados de 8 cm (región verde)	${ \color{red} {+} } {(8) = 32}$cm
Perímetro total:	$=2 \pi+32$cm
	$=38.28$cm

Área buscada:

Área del círculo (azul)	$\pi r^2 = \pi(1)^2 = \pi$
Más el área cuatro rectángulos $R_1$ (verde)	${ \color{red} {+} } {4 bh=4(1)(8)=32}$cm$^2$
Más el área del cuadrado $R_2$ (rojo)	${ \color{red} {+} } {l^2=(8)^2=64}$cm$^2$
Área total:	$= \pi + 32 + 64$cm$^2$
	$= \pi + 96$cm$^2$
	$99.14$cm$^2$

Regresa al principio del fichero para resolver la actividad 5

Letra C

Escribir

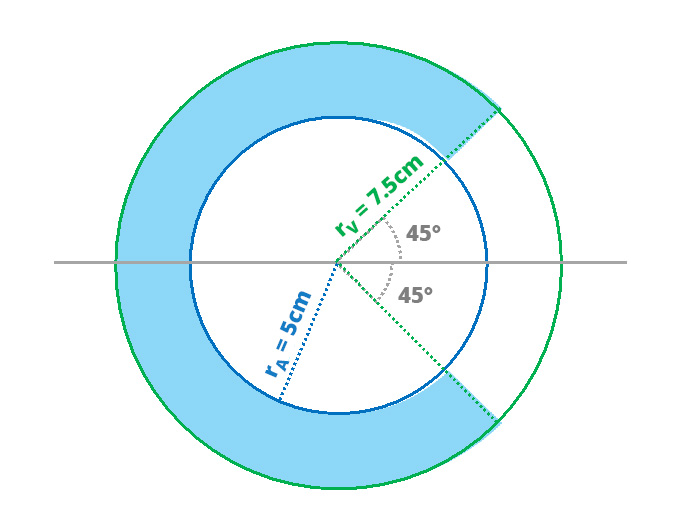
Determina el área y el perímetro de la región sombreada si radio del círculo interior es de 5 cm, el círculo exterior es de 7.5 cm, con las aberturas de los segmentos de 45° a cada lado de la horizontal.

Perímetro:	63.90 cm
Área:	73.63 cm$^2$

A partir de la figura, se calcula el perímetro y el área solicitados:

Definiciones, sea:

El ángulo que está sin rellenar es de 90° (que corresponde a una cuarta parte de la circunferencia y del círculo) por lo que el perímetro y el área corresponderán a ¾ de la figura completa.

Perímetro buscado:

¾ de la circunferencia exterior:	$( \tfrac {3}{4} ) 2 \pi r = 1.5 \pi (7.5) = 11.25 \pi$cm
¾ de la circunferencia interior:	${ \color{red} {+} } {( \tfrac {3}{4} ) 2 \pi r = 1.5 \pi (5) = 7.5 \pi}$cm
Dos segmentos de la diferencia de los radios entre ambas circunferencias	${ \color{red} {+} } {2(r_V-r_A)=2(7.5-5)=5}$cm
Perímetro total:	$=18.75 \pi+5$cm
	$=63.90$cm

Área buscada:

¾ del área del exterior	$( \tfrac {3}{4} ) \pi r^2 = ( \tfrac {3}{4} ) \pi(7.5)^2 = 42.1875 \pi$cm$^2$
–¾ del área del interior	${ \color{red} {-} } {( \tfrac {3}{4} ) \pi r^2 = ( \tfrac {3}{4} ) \pi(5)^2 = 18.75 \pi}$cm$^2$
Área total:	$= 42.1875 \pi – 18.75 \pi$cm$^2$
	$= 23.4375\pi$cm$^2$
	$73.63$cm$^2$

Fin de actividades finales

Para un triángulo, polígono regular de $n=3$ lados:
El cálculo del ángulo sería:	$$\alpha=\tfrac{360^o}{2(3)}=60^o$$
Por lo tanto, el área sería:	$$P_p=2(3)(sen 60^o)r$$ $$P_p=6(0.806025)r$$ $$P_p=5.196152r$$

Para un cuadrado, polígono regular de $n=3$ lados:
El cálculo del ángulo sería:	$$\alpha=\tfrac{360^o}{2(3)}=60^o$$
Por lo tanto, el área sería:	$$A_p=3(sen 60^o)(cos 60^o)r^2$$ $$A_p=3(0.806025)(0.5)r^2$$ $$A_p=1.299038r^2$$

Actividad final

Rectas y segmentos

Triángulo inscrito

Regiones

Cuadrado redondeado

Letra C

Síguenos

Sitios de interés

Nosotros

Escolares

Newsletter