Teorema
Refiere a que la razón entre la circunferencia y su diámetro es constante para todos los círculos.
Este teorema implica que dados dos círculos de diferentes circunferencias ($C_1$ y $C_2$) y, en consecuencia, diferentes diámetros ($2r_1$ y $2r_2$), entonces las razones $\tfrac{C_1}{2r_1}$ y $\tfrac{C_1}{2r_1}$ tienen un mismo valor, es decir:
$$\tfrac{C_1}{2r_1}=\tfrac{C_2}{2r_2}$$
El valor de esta razón constante es el número $π$.
El número $π$ se define como el cociente entre la circunferencia y el diámetro.
Medición del diámetro de una circunferencia

Revisa el recurso GeoGebra .
En la figura también puedes observar que el punto $X$ y la línea roja determinan el diámetro y el tamaño de la circunferencia. Compara el valor de diámetro $(d)$ con el de la circunferencia $(C)$ y realiza la división: $\frac{C}{d}$
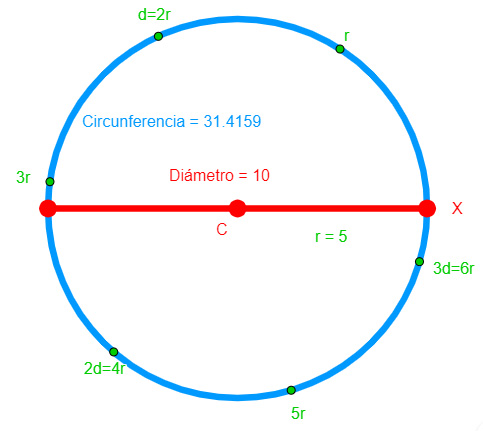
El número $π$ es un número irracional, por lo que posee infinitas cifras decimales no periódicas. Una aproximación de $\pi=3.14159265$…
A partir de la definición anterior se tiene la siguiente relación: $\pi=\tfrac{C}{d}=\tfrac{C}{2r}$, es decir, $C=2 \pi r$
Demostración - Por aproximaciones sucesivas
Para calcular el perímetro del círculo se debe considerar el siguiente teorema básico:
- Se crearán polígonos regulares de $n$ lados circunscritos en un círculo, las esquinas de los polígonos coincidirán con la circunferencia.
- Se calculará el área de los triángulos rectángulos como se muestran en la figura. La apotema ($a$) parte del centro del círculo a cada una de las bases inscritas, en cada uno de los $n$ triángulo isósceles se tendrán dos triángulos reflejados (congruentes); nota que se forman dos triángulos rectángulos en cada triángulo isósceles, por lo que se tendrán $2n$ triángulos rectángulos en cada polígono de $n$ lados.
A continuación se muestra el procedimiento para obtener el área de un triángulo rectángulo y de un cuadrado:
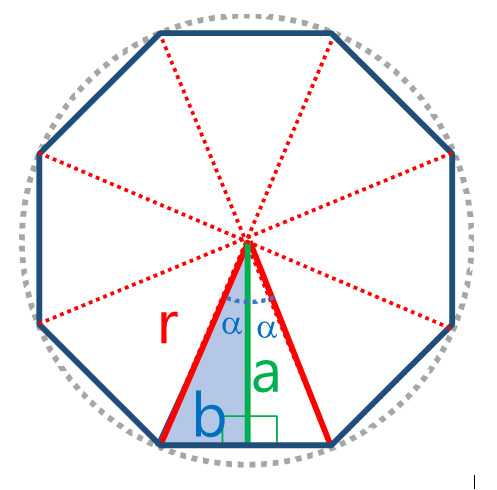
Procedimiento para el cálculo del área del triángulo rectángulo mostrado en la figura
- Se define un polígono regular de $n=4$ lados (cuadrado) inscrito en la figura:
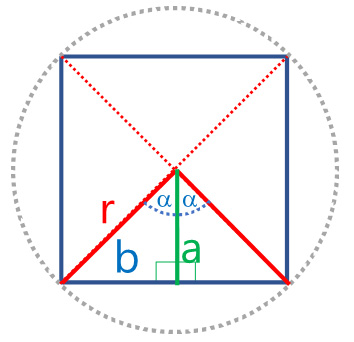
| Se forman $n=4$ triángulos isósceles, conformados por dos triángulos rectángulos con hipotenusa igual a $r$, un ángulo $α$ igual a la circunferencia dividida entre $n$=4 lados ($n=4$ triángulos isósceles) y, su vez, divididos entre $2$ | |
| por lo que el ángulo $\alpha$: | $$\alpha=\tfrac{360^o}{2n}$$ |
| El valor de la base del triángulo isósceles se puede calcular por razones trigonométricas: | $$\cos({\alpha})=\frac{Cateto \hspace{0.25em} Adyacente}{Hipotenusa}=\frac{a}{r}$$ |
| Por lo tanto, el valor de la base es: | $$b_{TR}=r \sin(\alpha)$$ |
| El valor de la base del triángulo isósceles, que es dos veces la del rectángulo: | $$P_p = 2n(\sin\alpha)r$$ Dónde: $n$ es el número de lados del polígono con el que deseamos aproximar la solución y $$\alpha=\tfrac{360^o}{2n}$$ |
| Para un cuadrado, polígono regular de $n=4$ lados: | 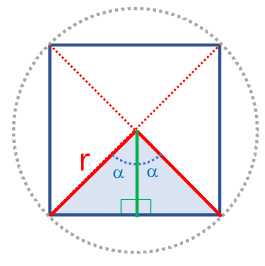 |
| El cálculo del ángulo sería: | $$\alpha=\tfrac{360^o}{2n}=45^o$$ |
| Por lo tanto, el área sería: | $$P_p=2(4)(\sin 45^o))r$$ $$P_p=8(0.7071)r$$ $$P_p=5.6568542r$$ |
| Para un cuadrado, polígono regular de $n=8$ lados: | 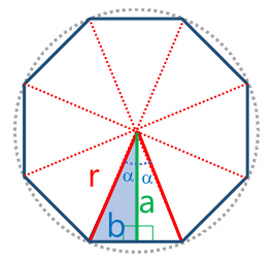 |
| El cálculo del ángulo sería: | $$\alpha=\tfrac{360^o}{2(8)}=22.5^o$$ |
| Por lo tanto, el área sería: | $$P_p=2(8)(\sin 22.5^o))r$$ $$P_p=16(0.382683)r$$ $$P_p=6.122935r$$ |
Termina fichero, realiza el ejercicio
Completa la siguiente tabla utilizando la fórmula que aparece a continuación. Puedes utilizar una calculadora científica o una hoja de cálculo (el ángulo debe estar en grados, no en radianes, para utilizar la expresión con radianes recuerda que $360^o=2π)$, recuerda que: $$P=2n \sin(\tfrac{360^o}{2n})r$$





