Tomando en cuenta la relación entre una función f(x) en un intervalo [a, b] y la Función Área A(x), que es una antiderivada para las funciones f(x) consideradas anteriormente, obtenidas con el límite de las aproximaciones de las sumas superiores e inferiores. Además, considerando especialmente la definición de la Integral Definida de una función, se establece el siguiente Teorema Fundamental del Cálculo:
Teorema Fundamental del Cálculo
Si $f(x)$ es una función continua en el intervalo $[a¸ b]$ , entonces la Integral Definida de $f(x)$ es $\int_{a}^{b}{f(x)dx}=F(b)-F(a)\$ , donde $F(x)$ es una antiderivada de $f(x)$, es decir $F'(x) = f(x)$
Justificación intuitiva del Teorema Fundamental del Cálculo
Esta justificación intuitiva y de manera gráfica se hace con el teorema del valor medio para integrales y la definición de Derivada de una función, por medio de los escenarios 1 y 2 de GeoGebra.
|
1. Teorema del valor medio para integrales: Si $f(x)$ es una función continua en el intervalo $a≤x≤b$,
entonces existe un número x_0 en el intervalo $a |
$\int_{a}^{b}{f\left(x\right)dx=(b-a)f(x_0)}$ |
|
2. Definición de Derivada una función $f(x)$: |
$f^\prime\left(x\right)=\lim_{h\rightarrow 0}{\frac{f\left(x+h\right)-f(x)}{h}}$ |
Al hacer clic en la siguiente liga se presenta el escenario Geogebra, parecido al mostrado, para que lo puedas explorar con detalle: Teorema del Valor Medio para Integrales. Posteriormente contesta las preguntas que aparecen en la tabla.
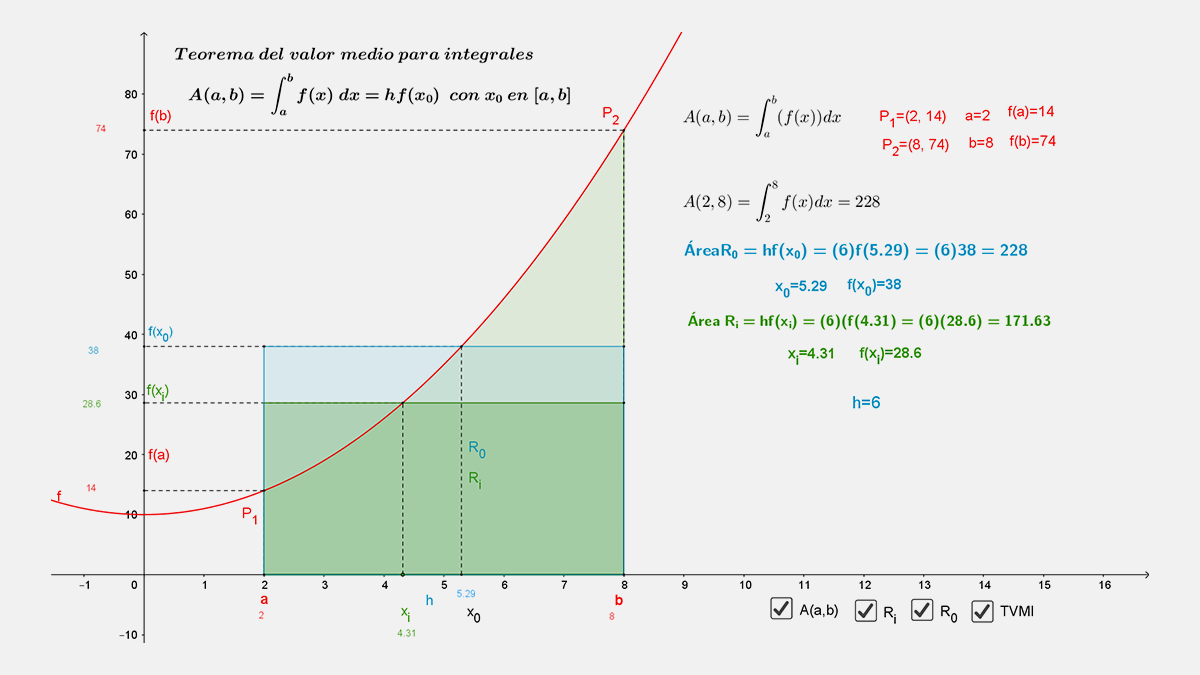

Explora cuidadosamente el Escenario 1 de Geogebra , activando y desactivando los diferentes botones las veces que sea necesario para observar los valores que se presentan, en particular cuando $h$ tiende a cero con el deslizador $h$. Considera que los valores son aproximados.
| 1. Puedes hacer coincidir aproximadamente su valor con el de la integral $\int_{a}^{b}{f(x)dx}$ |
|
| 2. Al activar el botón $R_0$, el valor de la integral $\int_{a}^{b}{f(x)dx}$ es igual a Área $R_0$? |
|
Al hacer clic en la siguiente liga se presenta el escenario Geogebra, parecido al mostrado, para que lo puedas explorar con detalle: Teorema Fundamental del Cálculo. Posteriormente contesta las preguntas que aparecen en la tabla.
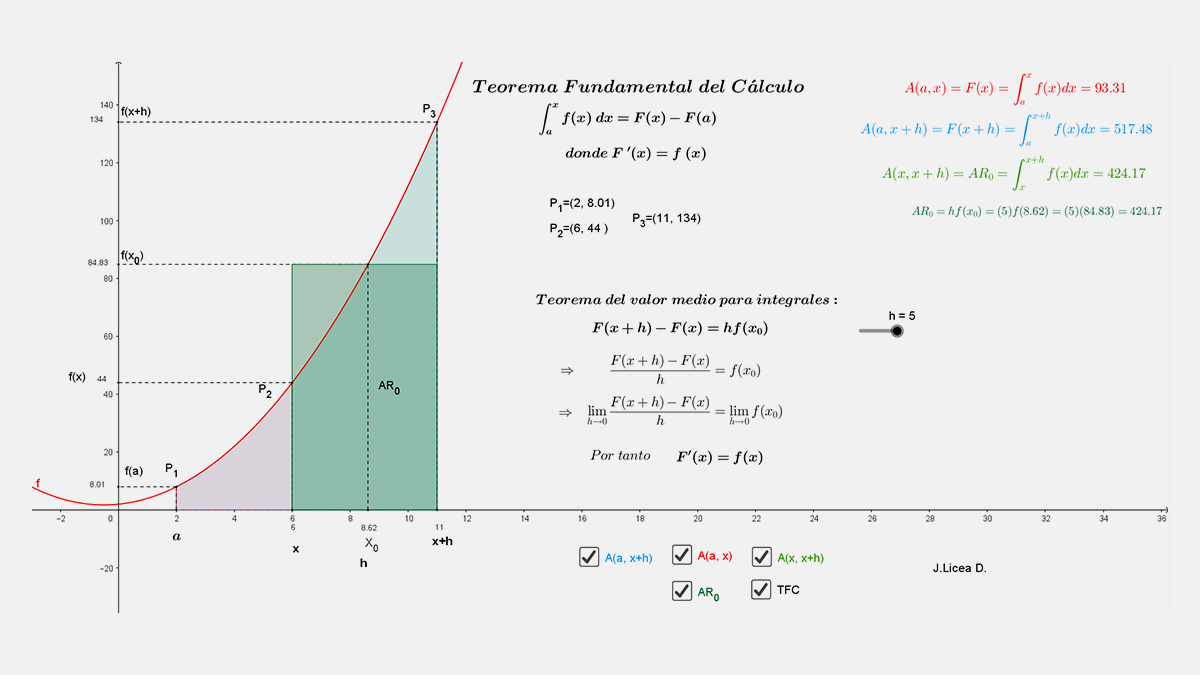

Explora cuidadosamente el Escenario 1 de Geogebra , activando y desactivando los diferentes botones las veces que sea necesario para observar los valores que se presentan, en particular cuando $h$ tiende a cero con el deslizador $h$. Considera que los valores son aproximados.
| 1. ¿$\lim_{h\rightarrow 0}{\frac{f\left(x+h\right)-f(x)}{h}}$ representa la Derivada de la función $f(x)$? |
|
| 2. ¿$\lim\below{h\rightarrow0}{f\left(x_0\right)}=\$ es el límite de $f(x)$? |
|


