Actividad final

Ejercicio de escritura

Con esta actividad aplicarás el Teorema Fundamental del Cálculo para resolver los siguientes problemas y ejercicios.

Problema 1

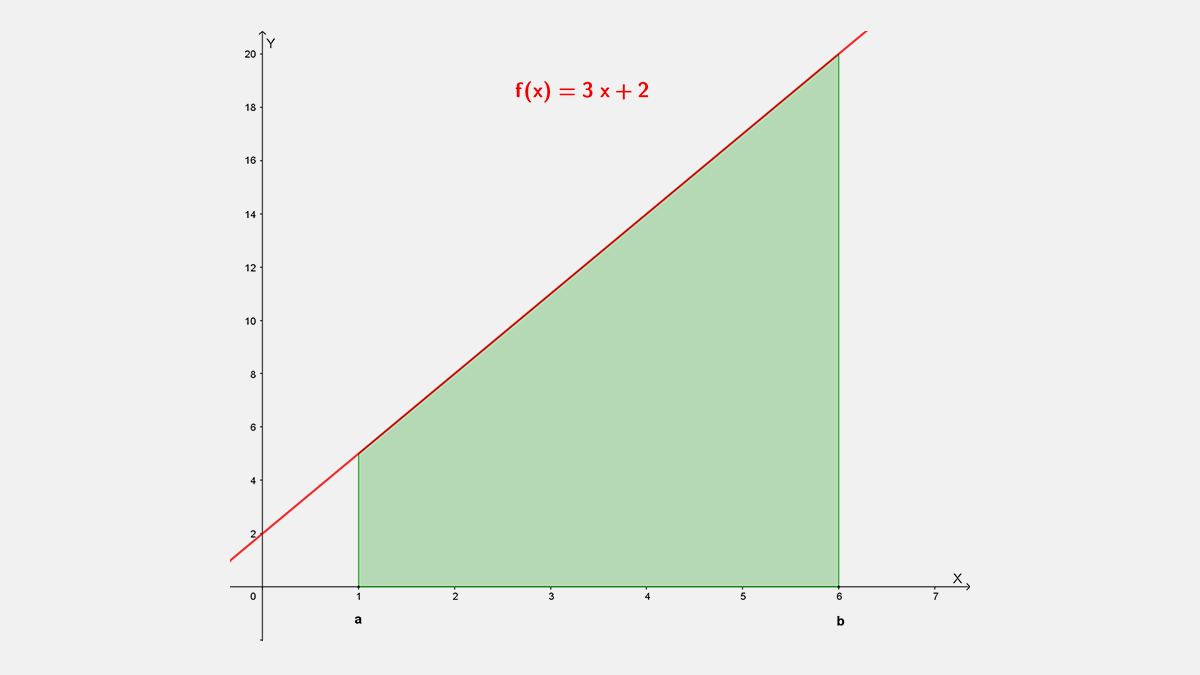
Área acotada de $f(x)=\ 3x+2$

Calcula el área bajo la gráfica de la función $f(x)=\ 3x+2$ y el eje “x”, de $x=1\quad a\quad x=6$, mostrada en la figura, a) geométricamente y b) con el Teorema Fundamental del Cálculo, para verificar que se obtienen los mismos resultados.

a) El área es:
62.5
b) El área es:
62.5

El área bajo la gráfica de la función $f(x)=\ 3x+2 $ y el eje “x”, de $x=1\quad a\quad x=6$, mostrada en la figura, se calcula geométricamente y con el Teorema Fundamental del Cálculo, para verificar que se obtienen los mismos resultados.

a) Geométricamente

La figura es un trapecio que se compone de un rectángulo de base 6-1=5 y altura 5, y un triángulo de base 6-1=5 altura 20-5=15

Área del rectángulo: $(base)(altura)=(5)(5)=25$

Área del triángulo: $\frac{(base)(altura)}{2}=\frac{(5)(15)}{2}=37.5$

Área total: $A_a^b =25+37.5=62.5$

b) Con el Teorema Fundamental del Cálculo

Como la función es positiva en el intervalo [2, 5], se puede calcular directamente con el Teorema como sigue:

$A_a^b=\int_{a}^{b}{f(x)dx}=F(b)-F(a) ,\quad donde\quad F^\prime\left(x\right)=f(x)$

con la función $f\left(x\right)=3x+2$ y su antiderivada $F\left(x\right)={\frac{3}{2}x}^2+2x,\quad con\quad a=1\ y\quad b=6$, se tiene que:

$F\left(6\right)={\frac{3}{2}(6)}^2+2\left(6\right)=54+12=66 \\F\left(1\right)={\frac{3}{2}(1)}^2+2\left(1\right)=1.5+2=3.5$

$A_1^6=\int_{1}^{6}{f(x)dx}=F\left(6\right)-F\left(1\right)=66-3.5=62.5$

Por lo que el área del trapecio es: $A_1^6=62.5$

Observa que se obtiene el mismo resultado del área del trapecio con el cálculo geométrico.

Para simplificar lo anterior, la Integral Definida se puede escribir como sigue:

$A_a^b=\int_{a}^{b}{f(x)dx}=\left. F(x)\right]_a^b=F\left(b\right)-F\left(a\right) , donde F^\prime\left(x\right)=f(x)$

con la función $f(x)=3x+2$ y su antiderivada $F(x)=〖3/2 x〗^2+2x$, $a=1$ y $b=6$ se tiene:

$A_1^6\int_{1}^{6}{(2x+5)dx}=\left. {\frac{3}{2}x}^2+2x\right]_1^6=\left[{\frac{3}{2}(6)}^2+2\left(6\right)\right]-\left[{\frac{3}{2}\left(1\right)}^2+2\left(1\right)\right]=\ 66-3.5=62.5$

Por lo que el área es: $A_1^6=62.5$

Problema 2

Se deja caer un objeto desde la azotea de un edificio. Si la velocidad del objeto en términos del tiempo $t$ que transcurre desde que se deja caer está dada por la función $v(t)=9.8t$, donde $t$ está dado en segundos y $v(t)$ está dada en metros/segundos, se quiere saber la altura del edificio si el objeto tarda 2.5 segundos en llegar al suelo.

La altura del edificio es:
30.625m

La altura del edificio es la distancia que recorre el objeto en su caída hasta llegar al suelo. Como la velocidad v(t) es la Derivada de distancia d(t), la antiderivada de la velocidad es la distancia.

Con el Teorema Fundamental del Cálculo se tiene que la distancia es:

$d(2.5)=\int_{0}^{2.5}{v\left(t\right)dt=\int_{0}^{2.5}{\left(9.8t\right)dt=\left. 4.9t^2\right]_0^{2.5}=\left[4.9{(2.5)}^2\right]-\left[4.9{(0)}^2\right]=\left[30.625\right]-\left[0\right]=}}30.625$

Por tanto la altura del edificio es 30.625 m

Problema 3

En una fábrica el costo marginal es $C^\prime\left(x\right)=60{(x-5)}^2$ pesos por unidad cuando el nivel de producción es x unidades ¿En cuánto aumentará el costo total de fabricación, si el nivel de producción aumenta de 10 a 15 unidades?

El aumento en el costo total de producción es:
$C=17 500 Pesos$

La figura muestra la gráfica del Costo Marginal de producción del problema cuya función es $C^' (x)=60〖(x-5)〗^2$ para x unidades producidas.

Como el Costo Marginal de producción $C^' (x)$ es la Derivada del Costo de producción $C(x)$, se tiene que Costo de producción es la Integral Definida de $C^'(x)$:

$C\left(x\right)=\int_{a}^{b}{C^\prime\left(x\right)dx}$

$C^\prime\left(x\right)=60{(x-5)}^2=60\left(x^2-10x+25\right)={60x}^2-600x+1500$

$C\left(x\right)=\int_{a}^{b}{({60x}^2-600x+1500)dx=\left. {\frac{60}{3}x}^3-{\frac{600}{2}x}^2+1500x\right]_{10}^{15}=\left[{\frac{60}{3}(15)}^3-{\frac{600}{2}(15)}^2+1500(15)\right]-\left[{\frac{60}{3}(10)}^3-{\frac{600}{2}(10)}^2+1500(10)\right]=\left[22500\right]-\left[5000\right]=17500$

Por tanto, el aumento en el costo de producción es $C=17 500 Pesos$

Problema 4

Consideremos que cuando tiene x años, cierta máquina industrial genera ingresos a la razón de $I^\prime\left(x\right)=6000-20x^2$ dólares por año y costos que se acumulan a la razón de $C^\prime\left(x\right)=3000+10x^2$ dólares por año.

  • a) Durante cuántos años es rentable el uso de la máquina.
  • b) ¿Cuál es la ganancia neta generada por la maquinaria durante el periodo del inciso a)?
La máquina es rentable durante:
10 años
Ganancia generada por la máquina es:
$G=20 000 Dólares$

Las gráficas de la razón de generación de ingresos y la razón en el aumento de los costos se tienen la figura.

Solución a)

El uso de la máquina es rentable cuando los ingresos son mayores que los costos, lo cual sucede cuando la razón de generación de ingresos es mayor a la razón en el aumento de los costos, desde t=0 hasta el punto de intersección de las gráficas, como se observa en la figura.

Para determinar el punto de intersección de las razones de Ingresos y de Costos, se igualan y se resuelve la ecuación resultante:

$I^\prime\left(x\right)=C\prime(x) \\6000-20x^2=3000+10x^2\\ 30x^2=3000\\ x^2=100 $

cuya solución es $t\ =10\ \ y\ \ t=\ -10\$, por lo que el valor con significado en el problema es $t =10$ que es el número de años por transcurrir (positivo).

Por tanto, la máquina es rentable durante 10 años.

Solución b)

La ganancia neta G es la diferencia del ingreso I menos el Costo C durante los 10 primeros años: $G=I-C$

El Ingreso y el costo se obtienen con la integral definida de $I^\prime\left(x\right)\quad y\quad C^\prime\left(x\right)$, de t=0 a t=10 años:

$I=\int_{0}^{10}{I^\prime\left(x\right)dx}\ y \ C=\int_{0}^{10}{C^\prime\left(x\right)dx}$

La Ganancia es $G=I-C=\int_{0}^{10}{I^\prime\left(x\right)dx}-\int_{0}^{10}{C^\prime\left(x\right)dx=\int_{0}^{10}\left[{I^\prime\left(x\right)-C}^\prime\left(x\right)\right]dx}$

Como ${I^\prime\left(x\right)-C}^\prime\left(x\right)=\left[6000-20x^2\right]-\left[3000+10x^2\right]=3000-30x^2 $

La Ganancia se puede obtener con

$G=\int_{0}^{10}{\left[3000-30x^2\right]dx=\left. 3000x-10x^3\right]_0^{10}=\left[3000(10)-10{(10)}^3\right]}-\left[3000\left(0\right)-10\left(0\right)^3\right]=30\ 000-10\ 000=20\ 000$

Por tanto la ganancia generada por la máquina es $G=20 000 Dólares$

Ejercicio de relación de columnas

Determina las siguientes integrales por medio del Teorema Fundamental del Cálculo, independientemente de lo que puedan representar. Algunas respuestas son aproximadas.

Integral Respuesta
1. $\int_{1}^{2.5}(5x-2x^{3})dx$
a) -5.91
2. $\int_{3}^{7}{\left(\sqrt x+x\right)dx\ \ }$
b) 28.88
3. $\int_{0}^{\frac{3\pi}{4}}{\left[cos(2x)\right]dx\ \ }$
c) 1/2
4. $\int_{0}^{\frac{\pi}{4}}{\left[{sec}^2(x)\right]dx\ \ }$
d) 1
5. $\int_{1}^{4}{\left(\frac{1}{x}\right)dx\ \ }$
e) 1.39
Opciones
d) 1
b) 28.88
a) -5.91
e) 1.39
c) 1/2