Problema 1
La velocidad de un automóvil en el arranque está dada por la función $v(t)=t^3+2t$ donde el t está en segundos y la velocidad está dada en metros ¿Qué distancia recorre en los primeros 4 segundos?
Como la derivada de la distancia d(t) es la velocidad v(t), entonces la antiderivada de la velocidad v(t) es la distancia, por lo que ésta es la integral de la velocidad. La figura muestra la gráfica de la velocidad del automóvil y el área señalada representa la distancia recorrida en los primeros 4 segundos.
La distancia recorrida $d_0^4$ con el Teorema Fundamental del Cálculo es:
$d_a^b=\int_{a}^{b}{v(t)dt}\left.=d(t)\right]_a^b=d(b)-d(a)$, donde $d^\prime\left(t\right)=v(t)$ en el intervalo [a, b]
para la función $v\left(t\right)=t^3+2t$ con antiderivada $d\left(t\right)=\frac{1}{4}t^4+t^2\$ de $a=0\quad y\quad b=4$
$d_0^4=\int_{0}^{4}{\left(t^3+2t\ \ \right)dt=}\left. \frac{1}{4}t^4+t^2\right]_0^4=\left[\frac{1}{4}{(4)}^4+{(4)}^2\ \ \right]-\left[\frac{1}{4}{(0)}^4+{(0}^2\ \ \right]$
$=\left[80\right]-\left[0\right]=80$
Por tanto la distancia recorrida es 80 m
Problema 2
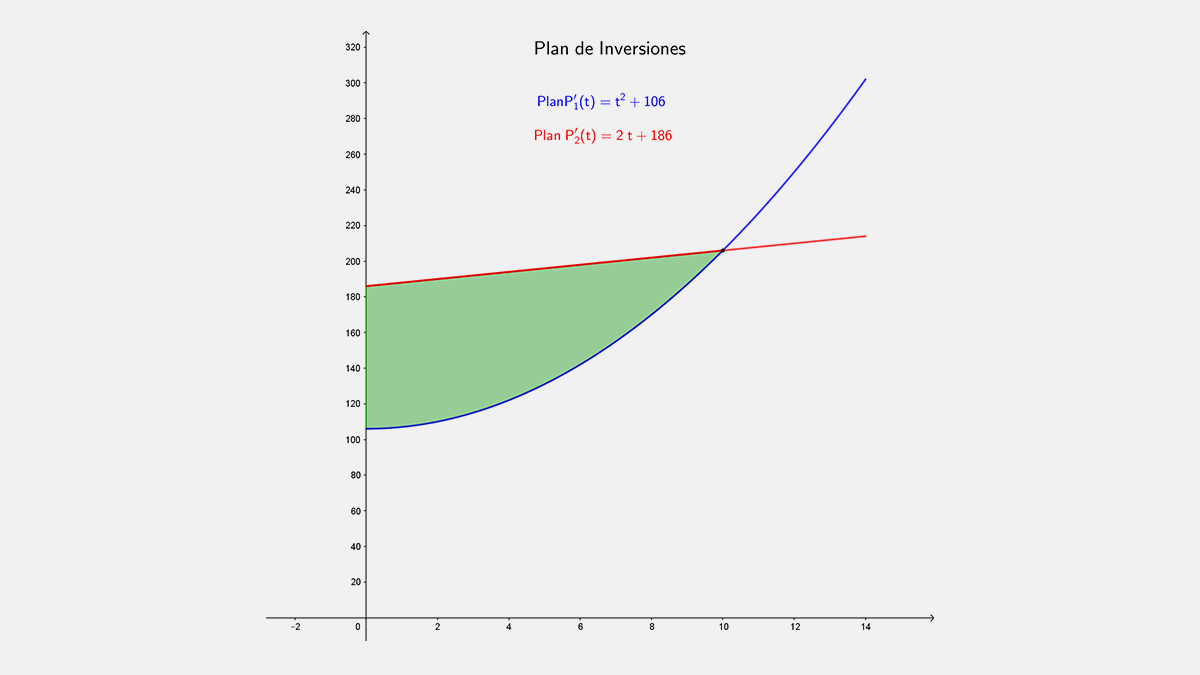
Un plan de inversión dentro t años generará utilidades a la razón $P_1^' (t)=t^2+106$ dólares al año, mientras que un segundo plan lo hará a la razón de $P_1^' (t)=2t+186$ dólares al año.
Solución. Las gráficas de las razones de rentabilidades se muestran en la figura, donde se observa que la razón de rentabilidad del plan $P_2 (t)$ es mayor que la rentabilidad del plan $P_1 (t)$ hasta se igualan en el punto de intersección.
Para determinar el punto de intersección de las rentabilidades, se igualan y se resuelve la ecuación resultante:
$P_1^\prime\left(t\right)=P_2^\prime(t)\quad\\ t^2+106=2t+186\\ t^2-2t-80=0\\ (t-10)(t+8)=0$
cuya solución es $t\ =10\ \ y\ \ t=\ -8$, por lo que el valor con significado en el problema es $t\ =10$ que es el número de años por transcurrir (positivo).
¿Cuánto exceso de utilidad ganará si invierte en el segundo plan en lugar del primero durante el periodo del inciso a)?
Para calcular cuánto es el exceso de utilidad del segundo plan se calculan las utilidades de los dos planes y se toma la diferencia hasta los 10 años $P_2(t)-P_1\left(t\right)$
El área entre las dos gráficas es el exceso de rentabilidad o utilidad de los dos planes.
Rentabilidad del Plan $P_1^' (t)$:
$P_1\left(t\right)=\int_{0}^{10}{P_1^\prime(t)}=\int_{0}^{10}\left(t^2+106\right)dt=\frac{1}{3}\left. t^3+106t\right]_0^{10}=\left[{\frac{1}{3}(10)}^3+106(10)\right]-\left[{\frac{1}{3}\left(0\right)}^3+106\left(0\right)\right]=\frac{1000}{3}+1060=1393.333,,,$
Rentabilidad del Plan $P_2^' (t)$:
$P_2\left(t\right)=\int_{0}^{10}{P_2^\prime(t)}=\int_{0}^{10}\left(2t+186\right)dt=\left. t^2+186t\right]_0^{10}=\left[{(10)}^2+186(10)\right]-\left[\left(0\right)^2+186\left(0\right)\right]=1960$
$P_2 (t)-P_1 (t)$=1960-1393.333=566.6666…
Por tanto, el exceso de rentabilidad es 566.66 Dólares, aproximadamente.
Problema 3
Una fuerza de 20 Newton comprime un resorte en 4 cm de su longitud natural de 30 cm. Determina el trabajo realizado para comprimir el resorte en 5 cm adicionales.
Solución. La ley de Hooke establece que la fuerza $F$ requerida para comprimir o estirar un resorte x unidades (de su longitud natural) es proporcional a la distancia x que el resorte es comprimido o estirado y está dada por la función $F(x)=kx$. Utilizando los datos del problema se tiene $4k = 20$, de donde $k = 5$ y la función fuerza es $F\left(x\right)=5x$, cuya representación gráfica se muestra en la figura.
El trabajo $T$ que se realiza es la fuerza $F$ que se aplica por el desplazamiento que se produce $x$:
$T=Fx$. Como en este problema la fuerza que se aplica para comprimir el resorte no es constante, sino sigue la Ley de Hooke $F(x)=kx$, donde k es la constante del resorte, el trabajo que produce que se produce está dado por la integral de la fuerza por el desplazamiento:
$T=\int_{a}^{b}F\left(x\right)dx$
Para saber la fuerza aplicada $F(x)=kx$ se toman los datos del problema: para x=5 cm la fuerza aplicada el 20 Newton, para determinar la constante k:
$k=F(x)/x=(20 N)/(4 cm)=5 N/cm$, por tanto la fuerza que se aplica es
$F\left(x\right)=5x$
Y el trabajo que se produce es:
$T=\int_{4}^{9}{(5x)dx}$
Con el Teorema Fundamental del Cálculo se determina la Integral Definida:
$T=\int_{4}^{9}{\left(5x\right)dx=\frac{5}{2}\left. x^2\right]_4^9=\left[\frac{5}{2}{(9)}^2\right]-\left[\frac{5}{2}\left(4\right)^2\right]=\left[202.5\right]-\left[40\right]=162.5}$
Por tanto el trabajo realizado es $T=162.5\ \frac{N}{cm}$