Como la velocidad no es constante, el cálculo de la distancia que recorre el objeto desde que se deja caer hasta llegar al suelo se hará por medio de aproximaciones, considerando constante la velocidad mayor y menor en cada intervalo.
-
Como una primera aproximación, el tiempo total de caída lo dividimos en 4 intervalos iguales y tomamos la velocidad mayor en cada intervalo como si fuera constante en todo ese intervalo. Esto se muestra en la figura siguiente:
• Intervalo 1: de t=0 s a t=1 s se toma velocidad constante v(1)=10(1)=10 km/h.
• Intervalo 2: de t=1 s a t=2 s se toma velocidad constante v(2)=10(2)=20 km/h.
• Intervalo 3: de t=2 s a t=3 s se toma velocidad constante v(3)=10(3)=30 km/h.
• Intervalo 4: de t=3 s a t=4 s se toma velocidad constante v(4)=10(4)=40 km/h.
La distancia recorrida por el objeto en cada intervalo la podemos calcular con el área señalada en ese intervalo, rectángulo superior, como se vio en el caso del automóvil de Enrique de velocidad constante, y una primera aproximación a la distancia recorrida total con la suma de las áreas de los rectángulos superiores de cada uno de los intervalos:
Área= 1(10)+1(20)+1(30)+1(40)=10+20+30+40=100
Por lo que la distancia total recorrida es aproximadamente 100 m.
Evidentemente esta distancia total es mayor que la real, puesto que tomamos como velocidad constante en cada intervalo la mayor de ese intervalo.
-
Otra posibilidad es tomar en cada uno de los 4 intervalos como constante la velocidad menor que se tiene en cada intervalo, rectángulo inferior. La distancia total recorrida es la suma de las áreas de los rectángulos inferiores en cada intervalo, como se muestra en la figura.
Área= 1(0)+1(10)+1(20)+1(30) =0+10+20+30=60.
Por lo que la distancia total recorrida es aproximadamente 60 km.
Nota que el “rectángulo” del primer intervalo tiene altura cero y por tanto área cero por lo que parece que solo se tienen tres rectángulos, pero diremos que son cuatro en nuestra contabilidad.
También, es evidentemente que esta distancia total es menor que la real, puesto que tomamos como velocidad constante en cada intervalo la menor de ese intervalo.
-
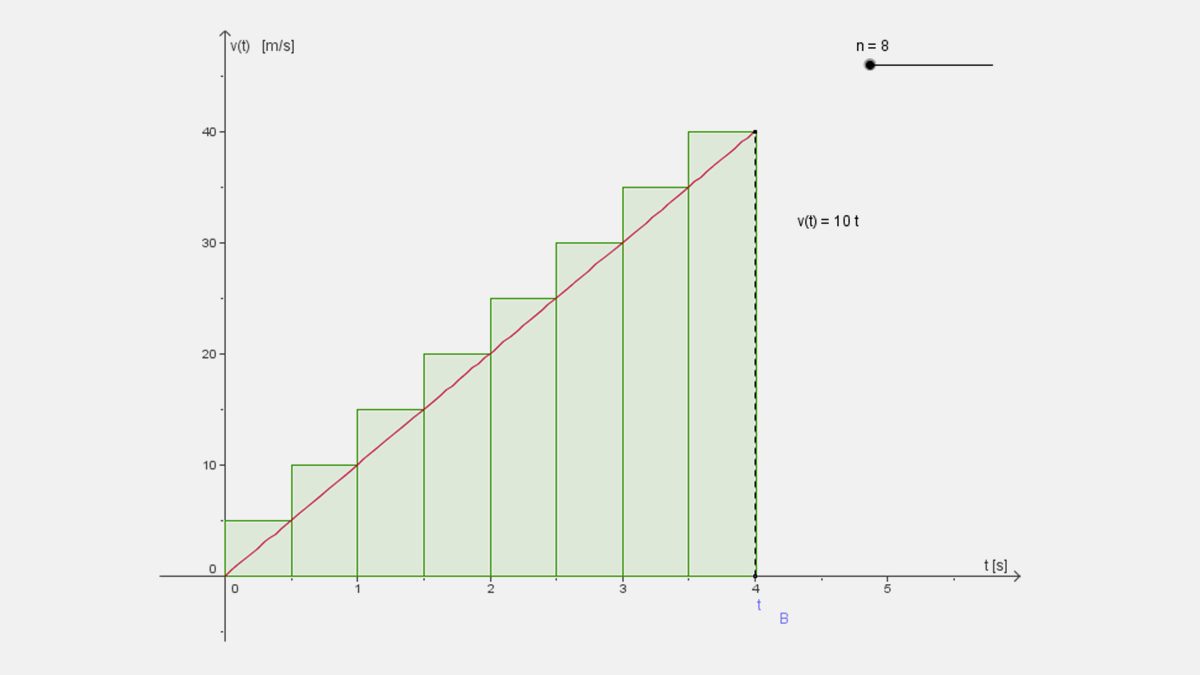
Una mejor aproximación es dividir a la mitad cada intervalo, es decir, con 8 rectángulos y seguir un procedimiento similar como el anterior, como se muestra a continuación.
El Área aproximada señalada, con n = 8 rectángulos superiores de t=0 a t=4, la representamos como ${\bar{A}}_0^4\left(n\right)={\bar{A}}_0^4\left(8\right)$
Esta área con v(t)=10t y n=8 el número de rectángulos del tiempo t=0 a t= 4 s se puede escribir de la siguiente forma:
Base de cada rectángulo: $\frac{4}{n}=\frac{4}{8}$
Altura del rectángulo i: $v(t_{i})=v(i\cdot \frac{4}{8})=10(i\cdot \frac{4}{8})$ donde el tiempo $t_i=i\cdot\frac{4}{8}$ con $i=1,\ 2,\ 3,\ \ldots\ ,8$
Nota que la velocidad $v(t_i)$ es la mayor de cada intervalo.
Por ejemplo, si i=3 se tiene $t_i=i∙4/8=3∙4/8=1.5$ y la altura del tercer rectángulo es $v(t_{3})=v(3\cdot \frac{4}{8})=10(3\cdot \frac{4}{8})=10(1.5)=15$
El área aproximada con 8 rectángulos superiores es:
$\bar{A_{0}^{4}}(n))=\bar{A_{0}^{4}}(8)=\left ( \frac{4}{8} \right)\left [ v\left ( 1\cdot \frac{4}{8} \right ) \right ]+\left ( \frac{4}{8} \right)\left [ v\left ( 2\cdot \frac{4}{8} \right ) \right ]+\left ( \frac{4}{8} \right)\left [ v\left ( 3\cdot \frac{4}{8} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{4}{8} \right)\left [ v\left ( 8\cdot \frac{4}{8} \right ) \right ]=\left ( \frac{4}{8} \right)\left [ 10\left ( 1\cdot \frac{4}{8} \right ) \right ]+\left ( \frac{4}{8} \right)\left [ 10\left ( 2\cdot \frac{4}{8} \right ) \right ]+\left ( \frac{4}{8} \right)\left [ 10\left ( 3\cdot \frac{4}{8} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{4}{8} \right)\left [ 10\left ( 8\cdot \frac{4}{8} \right ) \right ]=\left ( \frac{4}{8} \right )^{2}10\left [ 1+2+3+\cdot \cdot \cdot +8 \right ]=\left ( \frac{1}{4} \right )10\left [ 36 \right ]=90$
Por tanto, el Área aproximada con n = 8 rectángulos superiores de t=0 a t=4 es 90 m.
-
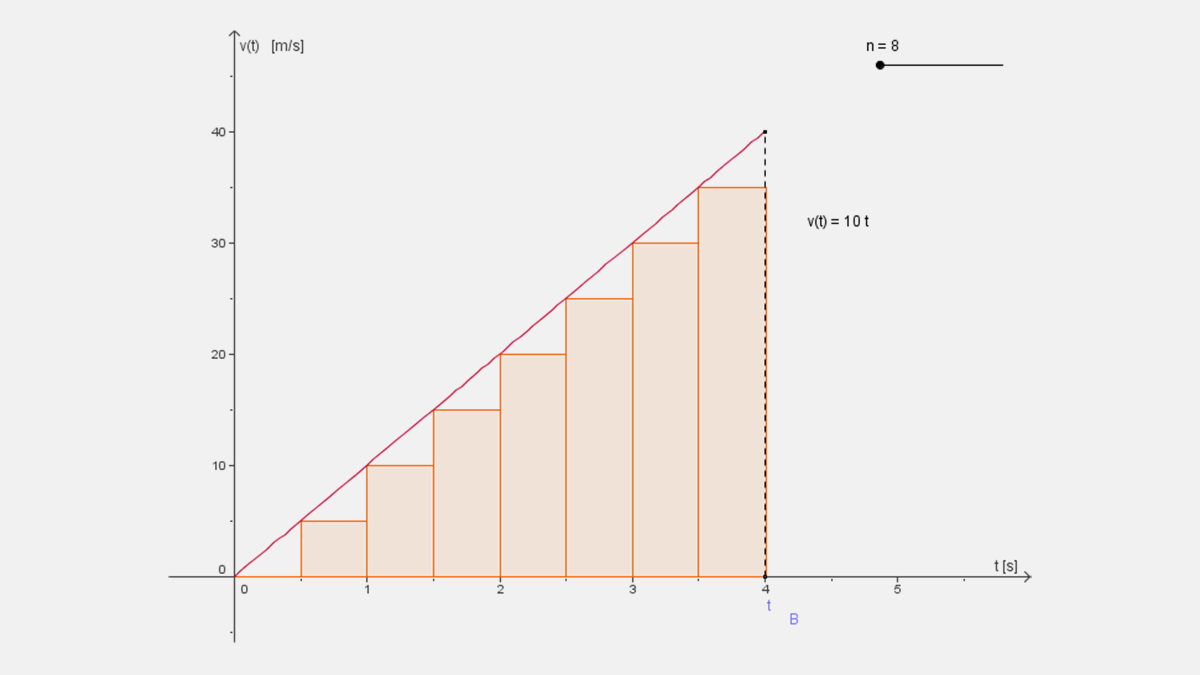
De manera similar se puede calcular el Área aproximada, con v(t)=10t y n=8 rectángulos inferiores de t=0 a t=4, ${\underline{A}\ }_0^4\left(n\right)=\ {\underline{A}\ }_0^4(8)$
Base de todos los rectángulos: 4/n
Altura del rectángulo 𝑖 : 𝑣𝑖=𝑣(𝑖−1)∙48=10(𝑖−1)∙48, donde el tiempo 𝑡𝑖 =(𝑖−1)∙48 con 𝑖=1, 2, 3, … ,8
Por ejemplo, si 𝑖 =3 se tiene t3=3−1∙48=2∙48=1 y la altura del tercer rectángulo es 𝑣3 =𝑣(3−1)∙48=102∙48101=10. Nota que la velocidad 𝑣𝑖 es la menor de cada intervalo. t3
El área aproximada con 8 rectángulos inferiores es:
$\underline{A} \;_{0}^{4}(8)=\left ( \frac{4}{8} \right)\left [ v\left ( 1-1\cdot \frac{4}{8} \right ) \right ]+\left ( \frac{4}{8} \right)\left [ v\left ( 2-1\cdot \frac{4}{8} \right ) \right ]+\left ( \frac{4}{8} \right)\left [ v\left ( 3-1\cdot \frac{4}{8} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{4}{8} \right)\left [ v\left ( 8-1\cdot \frac{4}{8} \right ) \right ]=\left ( \frac{4}{8} \right)\left [ 10\left ( 0\cdot \frac{4}{8} \right ) \right ]+\left ( \frac{4}{8} \right)\left [ 10\left ( 1\cdot \frac{4}{8} \right ) \right ]+\left ( \frac{4}{8} \right)\left [ 10\left ( 2\cdot \frac{4}{8} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{4}{8} \right)\left [ 10\left ( 7\cdot \frac{4}{8} \right ) \right ]=\left ( \frac{4}{8} \right )^{2}10\left [ 1+2+3+\cdot \cdot \cdot +7 \right ]=\left ( \frac{1}{4} \right )10\left [ 28 \right ]=70$
Por lo que el Área aproximada con n = 8 rectángulos inferiores de t=0 a t=4 es 70 m
Así, aunque no sabemos cuál es el área exacta A o distancia total real recorrida por el objeto hasta llegar al suelo, sabemos que está entre 70 m y 90 m, es decir,
70 m ≤ A ≤ 90 m
Se puede seguir haciendo cada vez mejores aproximaciones para calcular el Área con más y más rectángulos, hasta determinar el área exacta, por lo que vamos a generalizar el procedimiento descrito para cualquier número n de rectángulos (una partición de n intervalos de t=0 s a t=4 s) y con v(t)=10 t.
-
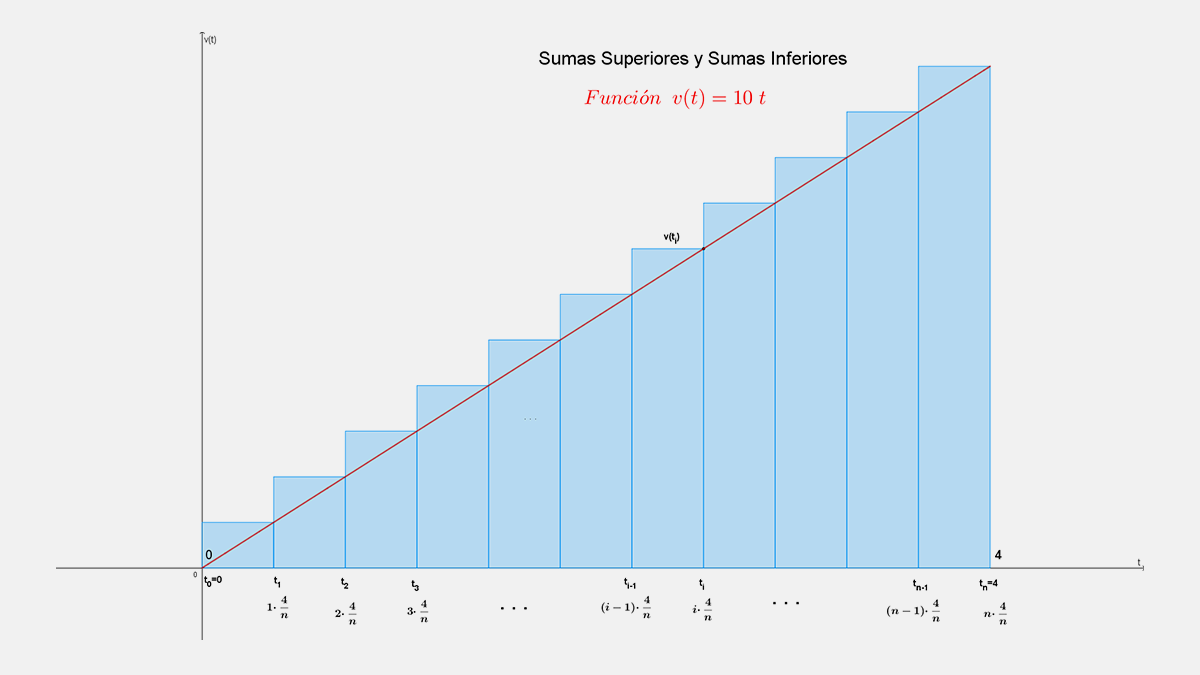
Generalización algebraica para calcular el área aproximada con n rectángulos superiores e inferiores y el área exacta
El Área aproximada con n rectángulos superiores de t=0 a t=4, la representamos como A ̅_0^4 (n). Esta área o también la distancia total recorrida, es la suma de las áreas de los rectángulos superiores en cada intervalo, como se muestra en la figura:
Esto se puede escribir de la siguiente forma, con v(t)=10t y n el número de rectángulos superiores en el tiempo t=0 a t= 4 s que dura la caída hasta llegar al suelo.
Base de todos los rectángulos: 4/n (Nota que solo se cambia el 8 anterior por n).
Altura del rectángulo i: $v\left(t_i\right)=v\left(i\cdot\frac{4}{n}\right)=10\left(i\cdot\frac{4}{n}\right)=10\left(i\cdot\frac{4}{n}\right) $, donde el tiempo t_i=i∙4/n y el área ${\overline{A}}_i=\left(\frac{4}{n}\right)\left[v\left(i\cdot\frac{4}{n}\right)\right]=\left(\frac{4}{n}\right)\left[10\left(i\cdot\frac{4}{n}\right)\right]$, con i=1,2,3,… ,n
Por ejemplo, la altura del rectángulo 3, i=3, es $v(t_3 )=v(3∙4/n)=10(3∙4/n)$
Y el área del rectángulo 3 es ${\overline{A}}_3=\left(\frac{4}{n}\right)\left[v\left(3\cdot\frac{4}{n}\right)\right]=\left(\frac{4}{n}\right)\left[10\left(3\cdot\frac{4}{n}\right)\right]$
El área aproximada con n rectángulos superiores ${\bar{A}}_0^4\left(n\right)$ es:
${\bar{A}}_0^4\left(n\right)={\overline{A}}_1+{\overline{A}}_2+{\overline{A}}_3+\ldots+{\overline{A}}_n$
$\bar{A_{0}^{4}}(n))=\left ( \frac{4}{n} \right)\left [ v\left ( 1\cdot \frac{4}{n} \right ) \right ]+\left ( \frac{4}{n} \right)\left [ v\left ( 2\cdot \frac{4}{n} \right ) \right ]+\left ( \frac{4}{n} \right)\left [ v\left ( 3\cdot \frac{4}{n} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{4}{n} \right)\left [ v\left ( n\cdot \frac{4}{n} \right ) \right ]=\left ( \frac{4}{n} \right)\left [ 10\left ( 1\cdot \frac{4}{n} \right ) \right ]+\left ( \frac{4}{n} \right)\left [ 10\left ( 2\cdot \frac{4}{n} \right ) \right ]+\left ( \frac{4}{n} \right)\left [ 10\left ( 3\cdot \frac{4}{n} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{4}{n} \right)\left [ 10\left ( n\cdot \frac{4}{n} \right ) \right ]=\left ( \frac{4}{n} \right )^{2}10\left [ 1+2+3+\cdot \cdot \cdot +n \right ]=\left ( \frac{16}{n^{2}} \right )10\left [ \frac{n(n+1))}{2} \right ]=\frac{160}{n^{2}}\left [ \frac{n^{2}+n}{2} \right ]=\frac{160n^{2}+160n}{2n^{2}}=80+\frac{80}{n}$
Nota: Se utilizó la fórmula $1+2+3+\ldots+n=\frac{n\left(n+1\right)}{2}=\frac{n^2+n}{2}$ para cualquier número natural n, por ejemplo, si n=8 la suma directa es $1+2+3+4+5+6+7+8=28$ y con la fórmula $\frac{n\left(n+1\right)}{2}= \frac{8\left(8+1\right)}{2}=\frac{8\left(7\right)}{2}=28$, se obtiene el mismo resultado.
Por tanto, el Área aproximada con n rectángulos superiores de t=0 a t=4 es:
$\bar{A_{0}^{4}}(n))=80+\frac{80}{n}$
-
Por ejemplo:
Si n= 4 se tiene $\bar{A_{0}^{4}}(4))=80+\frac{80}{4}=80+20=100$
Si n= 8 se tiene $\bar{A_{0}^{4}}(8))=80+\frac{80}{8}=80+80=90$
Que son los valores obtenidos antes.
El Área aproximada con n rectángulos inferiores de t=0 a t=4, la representamos como $\bar{A_{0}^{4}}(n))$. Esta área o también la distancia total recorrida, es la suma de las áreas de los rectángulos inferiores en cada intervalo, como se muestra en la figura:
De manera similar, se puede escribir de la siguiente forma con $v(t)=10t$ y n el número de rectángulos en el tiempo t=0 a t= 4 s que dura la caída hasta llegar al suelo:
Base de todos los rectángulos: 4/n
Altura del rectángulo 𝑖: $v\left(t_i\right)=v\left(i\cdot\frac{4}{n}\right)=10\left(i\cdot\frac{4}{n}\right)=10\left[i-1)\cdot\frac{4}{n}\right]$
donde el tiempo $t_i=(i-1)\cdot\frac{4}{n}$ con $i=1,2,3,… ,n$
Por ejemplo, la altura del rectángulo 3, i=3, es $v\left(t_3\right)=v\left((3-1)\cdot\frac{4}{n}\right)=10\left(2\cdot\frac{4}{n}\right)$
Nota que la velocidad $v(t_i )$ es la menor de cada intervalo.
El área aproximada con n rectángulos inferiores ${\underline{A}\ }_0^4\left(n\right)$ es:
$\underline{A} \;_{0}^{4}(n)=\left ( \frac{4}{n} \right)\left [ v\left ( (1-1)\cdot \frac{4}{n} \right ) \right ]+\left ( \frac{4}{n} \right)\left [ v\left ( (2-1)\cdot \frac{4}{n} \right ) \right ]+\left ( \frac{4}{n} \right)\left [ v\left ( (3-1)\cdot \frac{4}{n} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{4}{n} \right)\left [ v\left ( (n-1)\cdot \frac{4}{n} \right ) \right ]=\left ( \frac{4}{n} \right)\left [ 10\left ( 0\cdot \frac{4}{n} \right ) \right ]+\left ( \frac{4}{n} \right)\left [ 10\left ( 1\cdot \frac{4}{n} \right ) \right ]+\left ( \frac{4}{n} \right)\left [ 10\left ( 2\cdot \frac{4}{n} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{4}{n} \right)\left [ 10\left ( (n-1)\cdot \frac{4}{n} \right ) \right ]=\left ( \frac{4}{n} \right )^{2}10\left [ 1+2+3+\cdot \cdot \cdot +(n-1) \right ]=\left ( \frac{16}{n^{2}} \right )10\left [ \frac{(n-1)((n-1)-1))}{2} \right ]=\left ( \frac{160}{n^{2}} \right )\left [ \frac{n^{2}-n}{2} \right ]=\frac{160n^{2}-160n}{2n^{2}}=80-\frac{80}{n}$
Por tanto, el Área aproximada con n rectángulos inferiores de t=0 a t=4 es
$\underline{A} \;_{0}^{4}(n)=80-\frac{80}{n}$
Por ejemplo:
Si n= 4 se tiene $\underline{A} \;_{0}^{4}(4)=80-\frac{80}{4}$
Si n= 8 se tiene $\underline{A} \;_{0}^{4}(8)=80-\frac{80}{8} =80-10=70$
que también son los valores obtenidos antes.
En general el área exacta A o la distancia real recorrida con cualquier número n rectángulos de t=0 s a t=4 s cumple con la siguiente desigualdad:
${\underline{A}\ }_0^4\left(n\right)\le A\le\ \ {\bar{A}\ }_0^4\left(n\right)$
con ${\underline{A}\ }_0^4\left(n\right)=80-\frac{80}{n}$
${\bar{A\ }}_0^4\left(n\right)=80+\frac{80}{n}$
Por lo qu $80-\frac{80}{n}\ \le A\le\ 80+\frac{80}{n}$
Utiliza las fórmulas obtenidas para calcular las áreas con n rectángulos superiores e inferiores y completar la siguiente tabla:
Área de rectángulos inferiores ${\underline{A}\ }_0^4\left(n\right)=80-\frac{80}{n}\ \ m $
Área de rectángulos superiores ${\bar{A}\ }_0^4\left(n\right)=80+\frac{80}{n}\ \ m$
En los cuadros del último renglón de cada columna escribe el límite correspondiente, cuando el número de rectángulos n tiende a infinito:
Explora cuidadosamente los escenarios de GeoGebra, activando y desactivando los diferentes botones las veces que sea necesario para observar los valores que se presentan.
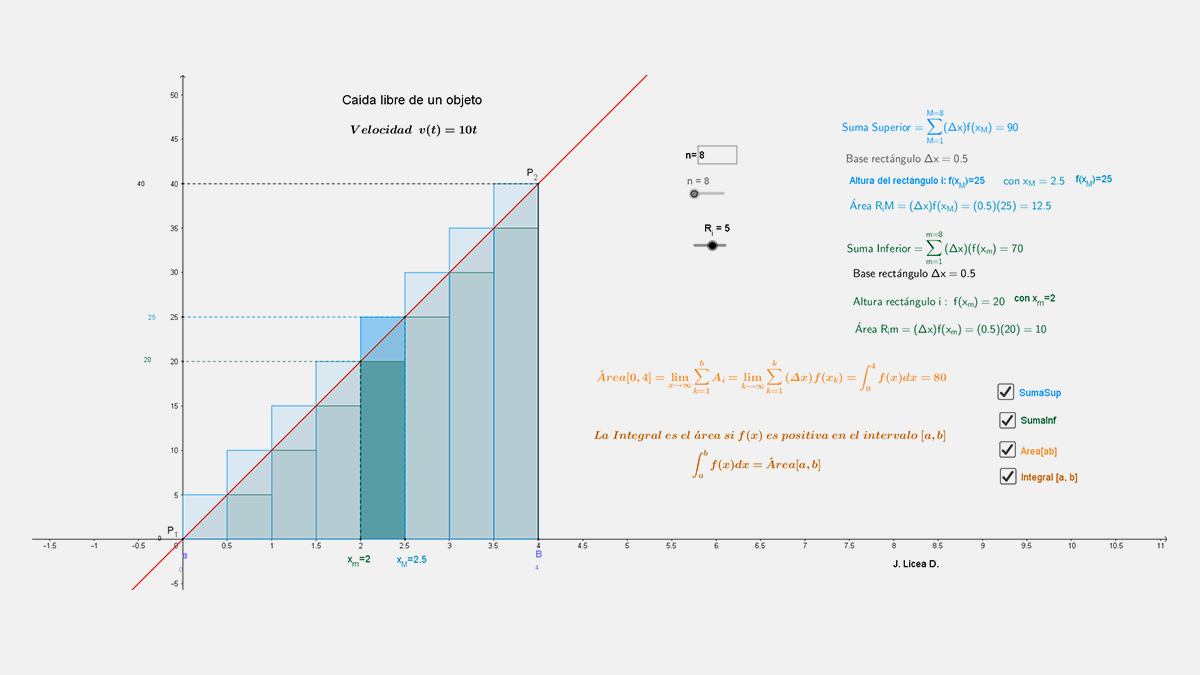
Al hacer clic en la siguiente liga se presenta el escenario GeoGebra html SUMA V(t)=10t, como el mostrado en la figura, en un recuadro grande para que el alumno lo pueda explorar con detalle.

En el recurso Geogebra , activando y desactivando los diferentes botones las veces que sea necesario para observar los valores que se presentan.
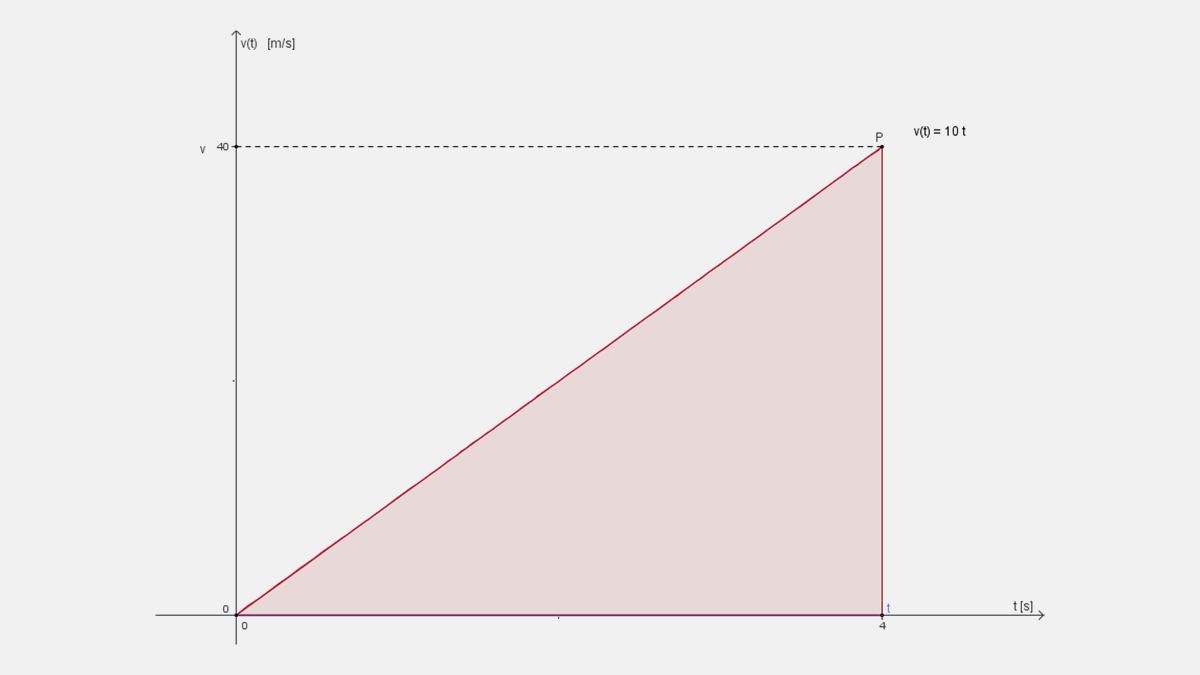
Por otra parte, observa que el límite de las aproximaciones con los rectángulos cuando su número n tiende a infinito es el área del triángulo de t=0 a t=4, mostrado en la siguiente figura:
Por lo que su Área se puede calcular con la fórmula conocida de la geometría elemental:
$Area\ A=(base)(altura)2=(4)(40)2=80$
Nota que efectivamente este valor es el límite de la suma de las áreas de los rectángulos, tanto superiores como inferiores, con el procedimiento de aproximaciones expuesto.
Ahora, para el área o distancia recorrida de $t=0$ a cualquier tiempo t es el área del rectángulo de base $t$ y altura $v(t)=10t$, se puede calcular de manera similar como:
$Area A=\frac{(base)(altura)}{2}=\frac{(t)(10t)}{2}=5t^{2}$
Por lo que el área es una función del tiempo t y se le llama Función Área: $A\left(t\right)=5t^2$
Con esta función la altura del edificio en el problema planteado se puede calcular con t=4 segundos, que es el tiempo que tarda el objeto en llegar al suelo:
La altura del edificio es A(4)=5(4)4=80m
Nota que es el mismo valor obtenido antes.
Para determinar esta función área con aproximaciones superiores e inferiores y el área exacta con el límite cuando n tiende a infinito con los procedimientos anteriores, al tiempo t no se le da un valor específico y de denota con t. Se obtiene:
Función Área $A\left(t\right)=5t^2 $
Función Área en el problema de caída libre, obtenida con el límite de aproximaciones, a cualquier tiempo t.
Si v(t)= 10t es la velocidad de un objeto en caída libre a cualquier tiempo t, siguiendo el procedimiento de aproximaciones se obtiene lo siguiente:
Área con n rectángulos superiores
Con n el número de rectángulos superiores (partición) en el tiempo de t=0 a t, se tiene:
Base de todos los rectángulos: t/n
Altura del rectángulo i : $v\left(t_i\right)=v\left(i\bullet\frac{t}{n}\right)=10\left(i\bullet\frac{t}{n}\right)=10\left[i\bullet\frac{t}{n}\right]$
donde el tiempo $t_i=i\cdot\frac{t}{n}$ con $i=1,2,3,… ,n$
Nota que solo cambia t=4 de los casos anteriores por t.
$\bar{A_{0}^{4}}(n))=\left ( \frac{t}{n} \right)\left [ v\left ( 1\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ v\left ( 2\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ v\left ( 3\cdot \frac{t}{n} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{t}{n} \right)\left [ v\left ( n\cdot \frac{t}{n} \right ) \right ]=\left ( \frac{t}{n} \right)\left [ 10\left ( 1\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ 10\left ( 2\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ 10\left ( 3\cdot \frac{t}{n} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{t}{n} \right)\left [ 10\left ( n\cdot \frac{t}{n} \right ) \right ]=\left ( \frac{t}{n} \right )^{2}10\left [ 1+2+3+\cdot \cdot \cdot +n \right ]=10\left ( \frac{t^{2}}{n^{2}} \right )\left [ \frac{n(n+1))}{2} \right ]=\frac{10t^{2}}{2}\left [ \frac{n^{2}+n}{n} \right ]=5t^{2}\left ( 1+\frac{1}{n} \right )$
Por lo que el Área aproximada con n rectángulos superiores de t=0 a t es
${\bar{A}}_0^t(n)=5t^2\left[1+\frac{1}{n}\right]\$
Área con n rectángulos inferiores
Con n rectángulos inferiores en el tiempo de t=0 a t, se tiene:
Base de todos los rectángulos: t/n
Altura del rectángulo i: ${\color{Red} v\left(t_i\right)=v\left(i\cdot\frac{t}{n}\right)=10\left(i\cdot\frac{t}{n}\right)=10\left[i-1)\cdot\frac{t}{n}\right]}$
donde el tiempo $t_i=(i-1)\cdot\frac{t}{n}$ con $i=1,\ 2,\ 3,\ \ldots\ ,n$
El área aproximada ${\underline{A}\ }_0^t$ es:
${\color{Red} {\underline{A}}\,_0^t(n))=\left ( \frac{t}{n} \right)\left [ v\left ( 0\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ v\left ( 1\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ v\left ( 2\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ v\left ( 3\cdot \frac{t}{n} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{t}{n} \right)\left [ v\left ( (n-1)\cdot \frac{t}{n} \right ) \right ]=\left ( \frac{t}{n} \right)\left [ 10\left ( 0\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ 10\left ( 1\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ 10\left ( 2\cdot \frac{t}{n} \right ) \right ]+\left ( \frac{t}{n} \right)\left [ v\left ( 3\cdot \frac{t}{n} \right ) \right ]+\cdot \cdot \cdot +\left ( \frac{t}{n} \right)\left [ 10\left ( (n-1)\cdot \frac{t}{n} \right ) \right ]=\left ( \frac{t}{n} \right )^{2}10\left [ 0+1+2+3+\cdot \cdot \cdot +(n-1) \right ]=10\left ( \frac{t^{2}}{n^{2}} \right )\left [ \frac{(n-1)n}{2} \right ] }$
Nota: Se utiliza la fórmula $1+2+3+\ldots+(n-1)=\frac{n^2-n}{2}$
Por tanto, el Área aproximada con n rectángulos inferiores de t=0 a t es
${\underline{A}\ }_0^t\left(n\right)=5t^2\left[1-\frac{1}{n}\right]\$
Como el área exacta A cumple con ${\color{Red} \lim_{n \to \infty}{\underline{A}\ }_0^t\left(n\right)\le \lim_{n \to \infty}A\le\ \ \lim_{n \to \infty}{\bar{A}}_0^t\left(n\right)}$
Para determinar el área exacta A, se obtiene el límite de las aproximaciones cuando el número de rectángulos tiende a infinito:
${\color{Red} \lim_{n \to \infty}{\underline{A}\ }_0^t\left(n\right)\le \lim_{n \to \infty}A\le\ \ \lim_{n \to \infty}{\bar{A}}_0^t\left(n\right)}$
Como
{\color{Red} \lim_{n \to \infty}{\bar{A}}_0^t\;(n))=\lim_{n \to \infty}5t^{2}\left [ 1+\frac{1}{n} \right ] =5t^{2}\left [ 1+0 \right ]=5t^{2}}
{\color{Red} \lim_{n \to \infty}\underline{A}\; _{0}^{t}(n)=\lim_{n \to \infty}5t^{2}\left [ 1-\frac{1}{n} \right ] =5t^{2}\left [ 1-0 \right ]=5t^{2}}
Se tiene $5t^2\le A\le\ \ 5t^2$
Por lo que el Área exacta de t=0 a t está dada por la:
Función Área $A(t)=5t^2$
En consecuencia, si la velocidad es $v(t)=10t$
la distancia que recorre el objeto es:
$d(t)=A(t)=5t^2$