Área acotada con $f(x)=x2$
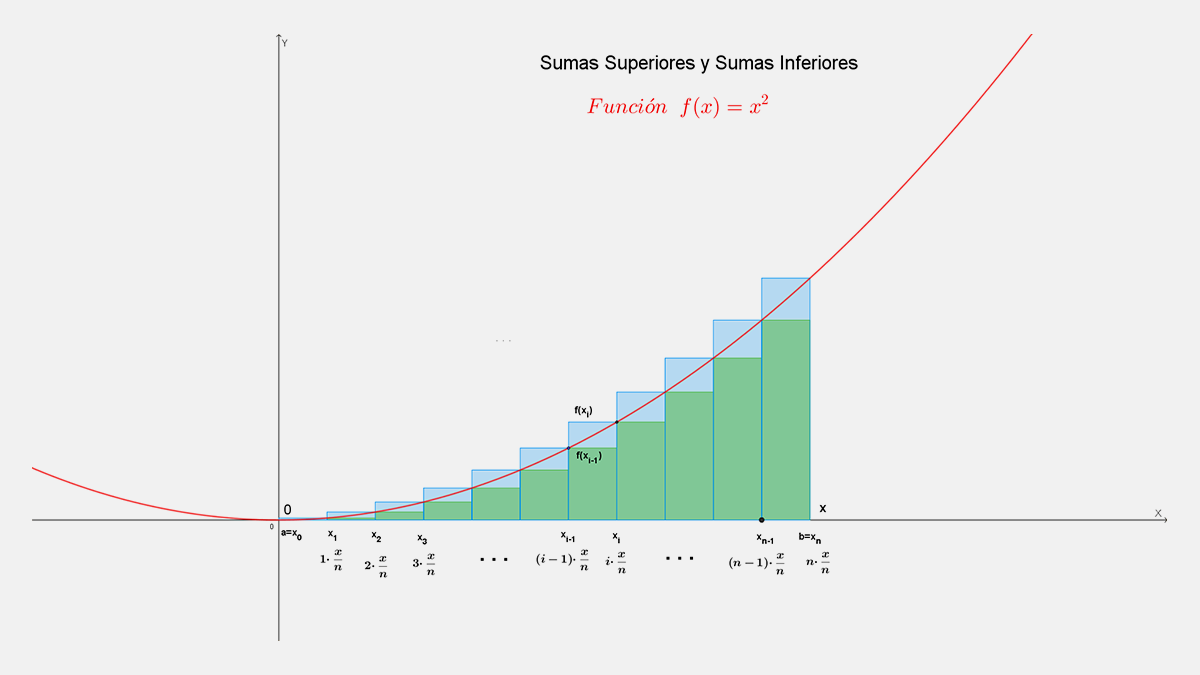
Para calcular esta área no se cuenta con una fórmula de la geometría elemental y se hará por el procedimiento de aproximaciones con rectángulos superiores e inferiores como en la sección previa, que muestra las ideas principales de la integral definida de una función.
-
Área para la función $f(x)=x2$ de x=0 a x=4 aproximada con n rectángulos superiores e inferiores
Los cálculos son similares a los anteriores y solo cambia la función por $f(x)=x^2$.
Para la función $ f(x)=x^2$ con n rectángulos superiores en el intervalo de x=0 a x=4, se tiene:
Base de todos los rectángulos: $4/n$
Altura del rectángulo $i$: $f(x_i )=f(i∙4/n)=(i∙4/n)^2$ donde $ x_i=i∙4/n$ con $i=1,2,3,… ,n$
Nota que la altura $f(x_i)$ es la mayor de cada intervalo.
${\bar{A}}_0^4\left(n\right)=\left(\frac{4}{n}\right)\left[f(1\cdot\frac{4}{n})\right]+\left(\frac{4}{n}\right)\left[f(2\cdot\frac{4}{n})\right]+\left(\frac{4}{n}\right)\left[f(3\cdot\frac{4}{n})\right]+\ \cdot\ \cdot\ \cdot\ +\left(\frac{4}{n}\right)\left[f(n\cdot\frac{4}{n})\right] \\ =\left(\frac{4}{n}\right)\left[\left[1\cdot\frac{4}{n}\right]^2\right]+\left(\frac{4}{n}\right)\left[\left[2\cdot\frac{4}{n}\right]^2\right]+\left(\frac{4}{n}\right)\left[\left[3\cdot\frac{4}{n}\right]^2\right]+\ \cdot\ \cdot\ \cdot\ +\left(\frac{4}{n}\right)\left[\left[n\cdot\frac{4}{n}\right]^2\right] \\ =\left(\frac{4}{n}\right)\left[{(1)}^2\left(\frac{4}{n}\right)^2\right]+\left(\frac{4}{n}\right)\left[{(2)}^2\left(\frac{4}{n}\right)^2\right]+\left(\frac{4}{n}\right)\left[{(3)}^2\left(\frac{4}{n}\right)^2\right]+\ \cdot\ \cdot\ \cdot\ +\left(\frac{4}{n}\right)\left[{(n)}^2\left(\frac{4}{n}\right)^2\right]$
$=\left(\frac{4}{n}\right)^3\left[1^2+2^2+3^2+\ \bullet\ \bullet\ \bullet\ +n^2\right]^\ast=\left(\frac{4}{n}\right)^3\left[\frac{n(n+1)(2n+1)\ }{6}\right]$
$=\frac{64}{n^3}\left[\frac{2n^3{+3n}^2+n\ }{6}\right]=\frac{128n^3+192n^2+64n}{6n^3}=\frac{64}{3}+\frac{32}{n}+\frac{32}{3n^2}$
$Por\ tanto\ \ \ \ {\bar{A}}_0^4\left(n\right)=\frac{64}{3}+\frac{32}{n}+\frac{32}{3n^2}$
*Nota: se utilizó la fórmula $1^2+2^2+3^2+\ \cdot\ \cdot\ \cdot\ +n^2=\frac{n(n+1)(2n+1)\ }{6}=\frac{2n^3{+3n}^2+n\ }{6} $
Por ejemplo, si n=4
$\begin{align*}{\bar{A}}_0^4\left(4\right)&=\frac{64}{3}+\frac{32}{n}+\frac{32}{3n^2}=\frac{64}{3}+\frac{32}{4}+\frac{32}{3{(4)}^2}=\frac{64}{3}+\frac{32}{4}+\frac{2}{3} \\&=\frac{256+96+8}{12}=\frac{360}{12}=\frac{180}{6}=30\end{align*}$
$\begin{align*} {\bar{A}}_0^4\left(8\right)&=\frac{64}{3}+\frac{32}{n}+\frac{32}{3n^2}=\frac{64}{3}+\frac{32}{8}+\frac{32}{3{(8)}^2}&=\frac{64}{3}+4+\frac{1}{6} =\frac{256+48+2}{12}=\frac{306}{12}=\frac{153}{6}=25.5\end{align*} $
Para la función $f(x)=x^2$ el número de n rectángulos inferiores, partición en el tiempo de x=0 a x=4, se tiene:
Base de todos los rectángulos: $4/n$
Altura del rectángulo $i$: $f\left(x_i\right)=f\left((n-i)\cdot\frac{4}{n}\right)=\left((n-i)\cdot\frac{4}{n}\right)^2$
con $i=1,2,3,… ,n$
Nota que la altura $f(x_i)$ es la menor de cada intervalo.
El cálculo es similar a lo anterior, pero la altura del primer rectángulo es
$f\left(x_1\right)=f\left((1-1)\bullet\frac{4}{n}\right)=\left((0)\bullet\frac{4}{n}\right)^2=0$
y la altura del último rectángulo es
$f\left(x_n\right)=f\left((n-1)\cdot\frac{4}{n}\right)=\left((n-1)\cdot\frac{4}{n}\right)^2$
${\underline{A}}_0^4\left(n\right)=\left(\frac{4}{n}\right)\left[f(0\bullet\frac{4}{n})\right]+\left(\frac{4}{n}\right)\left[f(1\bullet\frac{4}{n})\right]+\left(\frac{4}{n}\right)\left[f(2\bullet\frac{4}{n})\right]+\ \bullet\ \bullet\ \bullet\ +\left(\frac{4}{n}\right)\left[f((n-1)\bullet\frac{4}{n})\right] =\left(\frac{4}{n}\right)\left[\left[1\bullet\frac{4}{n}\right]^2\right]+\left(\frac{4}{n}\right)\left[\left[2\bullet\frac{4}{n}\right]^2\right]+\left(\frac{4}{n}\right)\left[\left[3\bullet\frac{4}{n}\right]^2\right]+\ \bullet\ \bullet\ \bullet\ +\left(\frac{4}{n}\right)\left[\left[(n-1)\bullet\frac{4}{n}\right]^2\right] =\left(\frac{4}{n}\right)\left[{(1)}^2\left(\frac{4}{n}\right)^2\right]+\left(\frac{4}{n}\right)\left[{(2)}^2\left(\frac{4}{n}\right)^2\right]+\left(\frac{4}{n}\right)\left[{(3)}^2\left(\frac{4}{n}\right)^2\right]+\ \bullet\ \bullet\ \bullet\ +\left(\frac{4}{n}\right)\left[{(n-1)}^2\left(\frac{4}{n}\right)^2\right]$
$=\left(\frac{4}{n}\right)^3\left[1^2+2^2+3^2+\ \bullet\ \bullet\ \bullet\ +{(n-1)}^2\right]^\ast=\left(\frac{4}{n}\right)^3\left[\frac{(n-1)(n-1+1)(2(n-1)+1)\ }{6}\right]$
$\\=\frac{64}{n^3}\left[\frac{2n^3{-3n}^2+n\ }{6}\right]=\frac{128n^3-192n^2+64n}{6n^3}=\frac{64}{3}-\frac{32}{n}+\frac{32}{3n^2}$
$Por\ tanto\ \ \ \ {\underline{A}\ }_0^4\left(n\right)=\frac{64}{3}-\frac{32}{n}+\frac{32}{3n^2}$
*Nota: se utilizó la fórmula $1^2+2^2+3^2+\ \bullet\ \bullet\ \bullet\ +n^2=\frac{n(n+1)(2n+1)\ }{6}$,con $n=n-1$
Por ejemplo, si $n=4$
${\underline{A}}_{\ 0}^{\ 4}\left(4\right)=\frac{64}{3}-\frac{32}{4}+\frac{32}{3\left(4\right)^2}=\frac{64}{3}-8+\frac{2}{3}=14$
Por ejemplo, si $n=8$
${\underline{A}}_{\ 0}^{\ 4}\left(8\right)=\frac{64}{3}-\frac{32}{8}+\frac{32}{3\left(8\right)^2}=\frac{64}{3}-4+\frac{1}{6}=17.5$
Por lo que el Área exacta A aproximada con n = 4 y 8 rectángulos superiores e inferiores de x=0 a x=4 está entre los siguientes valores:
$14 ≤ A ≤ 30$
$17.5 ≤ A ≤ 25.5$
El área exacta se determina con el límite de las aproximaciones cuando n tiende a infinito, como se muestra a continuación:
${\underline{A}\ }_0^4\left(n\right)\le A\le\ \ {\bar{A}\ }_0^4\left(n\right)$
$\lim_{n \to \infty}{\underline{A}\ }_0^4\left(n\right)\le \lim_{n \to \infty}A\le\ \ \lim_{n \to \infty}{\bar{A}}_0^4\left(n\right)$
Como
$\lim_{n \to \infty}{\underline{A}\ }_0^4\left(n\right)\ =\lim_{n \to \infty}\left[\frac{64}{3}+\frac{32}{n}+\frac{32}{3n^2}\right]\ =\lim_{n \to \infty}\left[\frac{64}{3}+32\left(\frac{1}{n}\right)+\frac{32}{3}\left(\frac{1}{n^2}\right)\right]=\frac{64}{3}+32\left(0\right)+\frac{32}{3}\left(0\right)=\frac{64}{3}+0+0=\frac{64}{3}$
$\lim_{n \to \infty}{\underline{A}\ }_0^4\left(n\right)\ =\lim_{n \to \infty}\left[\frac{64}{3}-\frac{32}{n}+\frac{32}{3n^2}\right]\ =\lim_{n \to \infty}\left[\frac{64}{3}-32\left(\frac{1}{n}\right)+\frac{32}{3}\left(\frac{1}{n^2}\right)\right]=\frac{64}{3}-32\left(0\right)+\frac{32}{3}\left(0\right)=\frac{64}{3}-0+0=\frac{64}{3}$
Se tiene
$\frac{64}{3}\le A\le\ \ \frac{64}{3}$
Por lo que el Área exacta de x=0 a x= 4 es:
$A=\frac{64}{3}=21.3333...$
Ejercicio de escribirAl hacer clic en la siguiente liga se presenta el escenario, parecido al mostrado en la figura, para que lo puedas explorar con detalle: SUMAS $f(x)=x^2$ – GeoGebra. Posteriormente contesta las preguntas que aparecen en la tabla.
Explora cuidadosamente los escenarios de Geogebra , activando y desactivando los diferentes botones las veces que sea necesario para observar los valores que se presentan.
-
Para $f(x)=x^2$, con n el número de rectángulos superiores de x=0 a x se sigue el procedimiento de los casos anteriores pero de manera general para cualquier número de rectángulos n y cualquier valor de x donde la función es positiva, sin darle un valor específico.
Base de todos los rectángulos: $\frac{x}{n}$
Altura del rectángulo $i$: $f\left(x_i\right)=f\left(i\bullet\frac{x}{n}\right)={(i\bullet\frac{x}{n})}^2$
donde $i=1,\ 2,\ 3,\ \ldots,n$ con $i=1,\ 2,\ 3,\ \ldots,n$
El área aproximada denotada por $A ̅_0^x (n)$ se obtiene de la siguiente manera;
${\bar{A}}_0^x\left(n\right)=\left(\frac{x}{n}\right)\left[f(1\cdot\frac{x}{n})\right]+\left(\frac{x}{n}\right)\left[f(2\cdot\frac{x}{n})\right]+\left(\frac{x}{n}\right)\left[f(3\cdot\frac{x}{n})\right]+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right)\left[f(n\cdot\frac{x}{n})\right] \\=\left(\frac{x}{n}\right)\left(1\cdot\frac{x}{n}\right)^2\ +\left(\frac{x}{n}\right)\left(2\cdot\frac{x}{n}\right)^2+\left(\frac{x}{n}\right)\left(3\cdot\frac{x}{n}\right)^2+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right)\left(n\cdot\frac{x}{n}\right)^2 \\=\left(\frac{x}{n}\right)1^2\left(\frac{x}{n}\right)^2\ +\left(\frac{x}{n}\right)2^2\left(\frac{x}{n}\right)^2+\left(\frac{x}{n}\right)3^2\left(\frac{x}{n}\right)^2+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right)n^2\left(\frac{x}{n}\right)^2 \\=\left(\frac{x}{n}\right)^3\left[1^2+2^2+3^2+\ \bullet\ \bullet\ \bullet\ +n^2\right]=\frac{x^3}{n^3}\left[\frac{n(n+1)(2n+1)\ }{6}\right]$
$=\frac{x^3}{n^3}\left[\frac{2n^3{+3n}^2+n\ }{6}\right]=x^3\left[\frac{2n^3{+3n}^2+n}{6n^3}\right]=x^3\left[\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}\right]$
Por tanto ${\bar{A}}_0^x\left(n\right)=x^3\left[\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}\right]$
Por ejemplo, si x=4 y n=8 se tiene sustituyendo estos valores:
${\bar{A}}_0^4\left(8\right)=4^3\left[\frac{1}{3}+\frac{1}{2(8)}+\frac{1}{6{(8)}^2}\right]=64\left[\frac{1}{3}+\frac{1}{16}+\frac{1}{384}\right]=25.5$
Por tanto ${\bar{A}}_0^4\left(8\right)=\frac{153}{6}=25.5$
Para $f(x)=x^2$, con n el número de rectángulos inferiores de x=0 a x, se tiene:
Base de todos los rectángulos: $\frac{x}{n}$
Altura del rectángulo $i$: $f\left(x_i\right)=f\left((i-1)\cdot\frac{x}{n}\right)=\left [\left(i-1\right)\cdot\left(\frac{x}{n}\right) \right ]^{2}$
donde el tiempo $x_i=i\bullet\frac{x}{n}$ con $i=1,\ 2,\ 3,\ \ldots\ ,n-1$
El área aproximada ${\underline{A}\ }_0^x\left(n\right)$ es:
${\underline{A}\ }_0^x\left(n\right)=\left(\frac{x}{n}\right)\left[f(0\cdot\frac{x}{n})\right]+\left(\frac{x}{n}\right)\left[f(1\cdot\frac{x}{n})\right]+\left(\frac{x}{n}\right)\left[f(2\cdot\frac{x}{n})\right]+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right)\left[f(n-1)\cdot\frac{x}{n}\right] =\left(\frac{x}{n}\right)\left(1\cdot\frac{x}{n}\right)^2\ +\left(\frac{x}{n}\right)\left(2\cdot\frac{x}{n}\right)^2+\left(\frac{x}{n}\right)\left(3\cdot\frac{x}{n}\right)^2+\ \cdot\ \cdot\ \cdot +\left(\frac{x}{n}\right)\left((n-1)\cdot\frac{x}{n}\right)^2 =\left(\frac{x}{n}\right)1^2\left(\frac{x}{n}\right)^2\ +\left(\frac{x}{n}\right)2^2\left(\frac{x}{n}\right)^2+\left(\frac{x}{n}\right)3^2\left(\frac{x}{n}\right)^2+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right){(n-1)}^2\left(\frac{x}{n}\right)^2 =\left(\frac{x}{n}\right)^3\left[1^2+2^2+3^2+\ \cdot\ \cdot\ \cdot\ +{(n-1)}^2\right]$
$=\frac{x^3}{n^3}\left[\frac{2n^3{-3n}^2+n\ }{6}\right]=x^3\left[\frac{2n^3{-3n}^2+n}{6n^3}\right]=x^3\left[\frac{1}{3}-\frac{1}{2n}+\frac{1}{6n^2}\right]$
Por tanto ${\underline{A}\ }_0^x\left(n\right)=x^3\left[\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}\right]$
Por ejemplo, si x=4 y n=8
${\underline{A}\ }_0^4\left(4\right)=4^3\left[\frac{1}{3}-\frac{1}{2(8)}+\frac{1}{6{(8)}^2}\right]=64\left[\frac{1}{3}-\frac{1}{16}+\frac{1}{384}\right]=17.5$
Por tanto ${\underline{A}\ }_0^4\left(8\right)=17.5$
El área exacta A se encuentra entre los siguientes valores: ${\underline{A}\ }_0^4\left(8\right)\le A\le\ \ {\bar{A}}_0^4\left(8\right)$
$17.5\le A\le\ 25.5$
El área exacta A(x) se obtiene con el límite de las aproximaciones inferiores y superiores cuando n tiende a infinito, como se muestra a continuación:
${\underline{A}\ }_0^x\left(n\right)\le{A\ }_0^4(x)\le\ \ {\bar{A}\ }_0^x\left(n\right)$
$\lim_{n \to \infty}{\underline{A}\ }_0^x\left(n\right)\le \lim_{n \to \infty}A\le\ \ \lim_{n \to \infty}{\bar{A}}_0^x\left(n\right)$
donde
Área superior: ${\bar{A}\ }_0^x\left(n\right)=x^3\left[\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}\right]$
Área inferior: $〖▁A 〗_0^x (n)=x^3 [1/3-1/2n+1/(6n^2 )]$
$\lim_{n \to \infty}{\bar{A}}_0^4\;(n) =\lim_{n \to \infty}\left [ x^{3}\left[\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}\right] \right ] =\lim_{n \to \infty}x^{3}\left[\frac{1}{3}+\frac{1}{2}\left(\frac{1}{n}\right)+\frac{1}{6}\left(\frac{1}{n^2}\right)\right]=x^{3}\left [ \frac{1}{3}+\frac{1}{2}(0)+\frac{1}{6}(0)\right ]=\frac{1}{3}x^{3}$
$\lim_{n \to \infty}{\underline{A}\ }_0^x\left(n\right) =\lim_{n \to \infty}\left [ x^{3}\left[\frac{1}{3}-\frac{1}{2n}+\frac{1}{6n^2}\right] \right ] =\lim_{n \to \infty}x^{3}\left[\frac{1}{3}-\frac{1}{2}\left(\frac{1}{n}\right)+\frac{1}{6}\left(\frac{1}{n^2}\right)\right]=x^{3}\left [ \frac{1}{3}-\frac{1}{2}(0)+\frac{1}{6}(0)\right ]=\frac{1}{3}x^{3}$
Se tiene que
$\lim_{n \to \infty}{\underline{A}\ }_0^x\left(n\right)\le \lim_{n \to \infty}A_0^x \ \lim_{n \to \infty}{\bar{A}}_0^4\left(n\right)$
$\frac{1}{3}x^3\le{A\ }_0^x(x)\le\ \ \frac{1}{3}x^3$
Por lo que el área exacta bajo la gráfica de la función $f(x)=x^2$ de x=0 a x está dada por la
Función Área: ${A\ }_0^x(x)=\frac{1}{3}x^3$
El área exacta A(x) para f(x)=x^2 de x=0 a x=4 es:
$A(4)=\frac{1}{3}{(4)}^3=\frac{64}{3}=21.333$
Si se quiere calcular el área exacta bajo la gráfica de la función $f(x)=x^2$, señalada en la figura, de x=2 a x=5 , se puede obtener con la función área como sigue:

Como el área de x=0 a x es $A(x)=\frac{1}{3}x^3$
Si x=2, el área exacta de x=0 a x=2 es Área $Area \quad A(2)=\frac{1}{3}{(2)}^3=\frac{8}{3}=2.666 \ \ldots\$
Si x=5, el área exacta de x=0 a x=5 es Área $A(5)=\frac{1}{3}{(5)}^3=\frac{125}{3}=41.666\ \ldots\$
Por lo que el área exacta de x=2 a x=5 denotada por $A_2^5$ es:
$A_2^5 = A(5) – A(2) = 39$
En general para calcular el área exacta bajo la gráfica de la función $f(x)=x^2 \ de\ x=a\ hasta\ x=b$, se obtiene con la Función Área $A(x)= \frac{1}{3}x^3$ y con esta:
${A\ }_a^b= A(x)]ab =A(b)-A(a)=\frac{1}{3}b^3-\frac{1}{3}a^3$
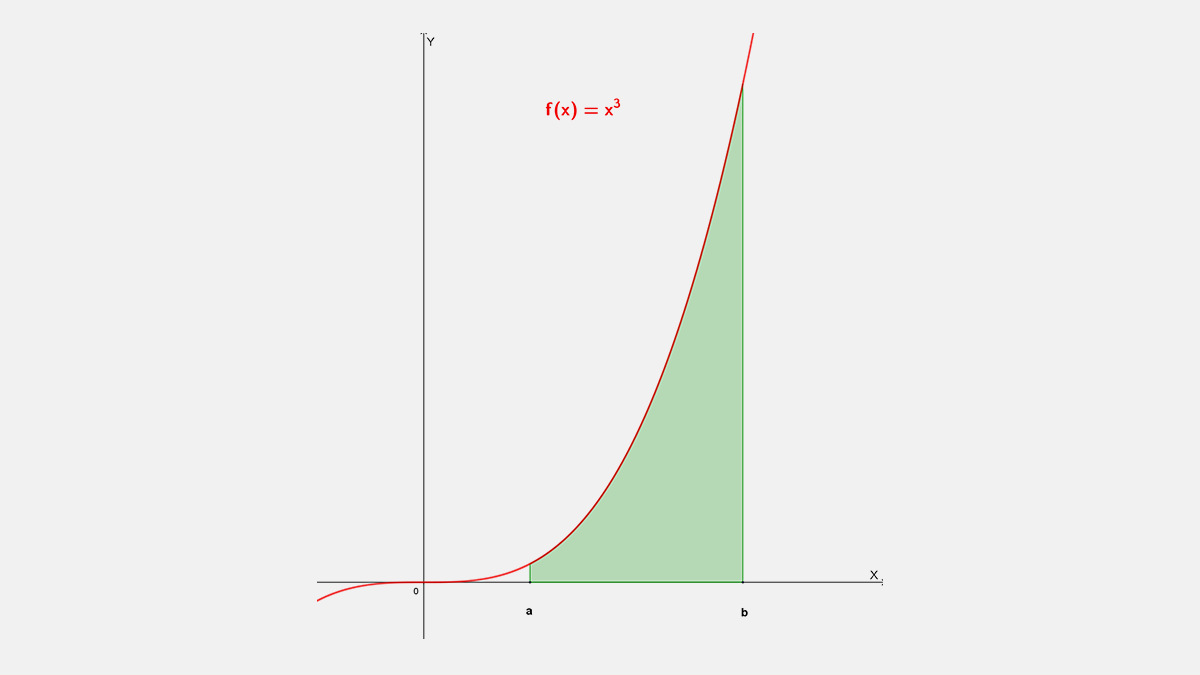
Área acotada de $f(x)=x^3$
Al hacer clic en la siguiente liga se presenta el escenario Geogebra, parecido al mostrado en la figura, para que lo puedas explorar con detalle: Área de $f(x)=x^$ – GeoGebra. Posteriormente contesta las preguntas que aparecen en la tabla.

Explora cuidadosamente el escenario de Geogebra , activando y desactivando los diferentes botones, las veces que sea necesario, para observar los valores que se presentan. (De manera similar a como se hizo con los escenarios SUMA $v(t)=10t$ y SUMA $f(x)=x2)$. Contesta las preguntas que se plantean
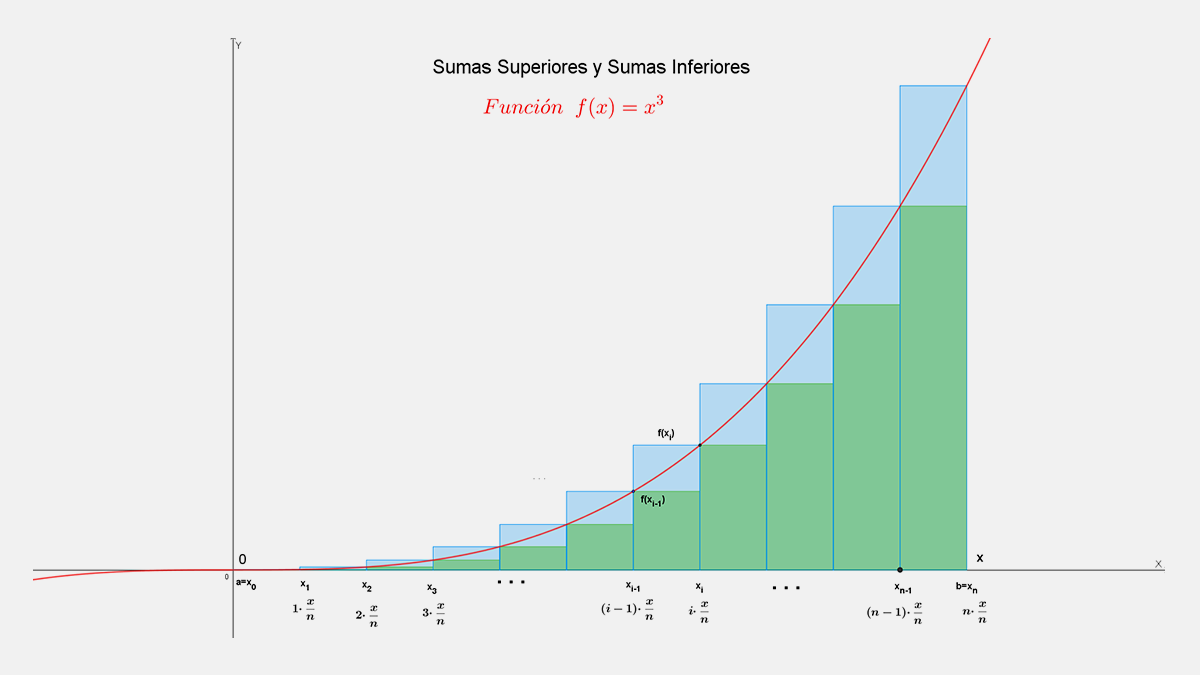
Función Área para la función $f(x)=x^3$
Siguiendo los procedimientos anteriores para determinar el área aproximada para la función f(x)=x^3 de x=0 a x con n rectángulos superiores e inferiores y el área exacta con los límites correspondientes cuando n tiende a infinito, se obtiene la función área.
Función Área ${A\ }_a^b= A(x)]ab =A(b)-A(a)=\frac{1}{4}b^4-\frac{1}{4}a^4$
Y el Área exacta para la función $f(x)=x^3$ de x=a a x=b, ver figura, se obtiene con la Función Área como:
${A\ }_a^b= A(x)]ab =A(b)-A(a)=\frac{1}{4}b^4-\frac{1}{4}a^4$
Para $f(x)=x^3$, con n el número de rectángulos superiores, de x=0 a x se siguen los procedimientos anteriores, donde solo se cambia la función.
Se tiene:
Base de todos los rectángulos:
Altura del rectángulo $i$: $f\left(x_i\right)=f\left(i\cdot\frac{x}{n}\right)={(i\cdot\frac{x}{n})}^3$
donde $x_i=i\cdot\frac{x}{n}$ con $i=1,\ 2,\ 3,\ \ldots\ ,n$
El área aproximada ${\bar{A}}_0^x\left(n\right)$ es:
${\bar{A}\ }_0^x\left(n\right)=\left(\frac{x}{n}\right)\left[f(1\cdot\frac{x}{n})\right]+\left(\frac{x}{n}\right)\left[f(2\cdot\frac{x}{n})\right]+\left(\frac{x}{n}\right)\left[f(3\cdot\frac{x}{n})\right]+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right)\left[f(n\cdot\frac{x}{n})\right] =\left(\frac{x}{n}\right)\left(1\cdot\frac{x}{n}\right)^3\ +\left(\frac{x}{n}\right)\left(2\cdot\frac{x}{n}\right)^3+\left(\frac{x}{n}\right)\left(3\cdot\frac{x}{n}\right)^3+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right)\left(n\cdot\frac{x}{n}\right)^3 =\left(\frac{x}{n}\right)1^3\left(\frac{x}{n}\right)^3\ +\left(\frac{x}{n}\right)2^3\left(\frac{x}{n}\right)^3+\left(\frac{x}{n}\right)3^3\left(\frac{x}{n}\right)^3+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right)n^3\left(\frac{x}{n}\right)^3$
${\bar{A}}_0^x\left(n\right) =\left(\frac{x}{n}\right)^4\left[1^3+2^3+3^3+\ \cdot\ \cdot\ \cdot\ +n^3\right]=\frac{x^4}{n^4}\left[\frac{n(n+1)\ }{2}\right]^2=\frac{x^4}{n^4}\left[\frac{n^4+2n^3+n^2}{4}\right] =x^4\left[\frac{n^4+2n^3+n^2}{4n^4}\right]=x^4\left[\frac{1}{4}+\frac{1}{2n}+\frac{1}{4n^2}\right]$
Se utiliza la fórmula $1^3+2^3+3^3+\ldots+n^3=\left[\frac{n\left(n+1\right)}{2}\right]^2=\left[\frac{n^2+n}{2}\right]^2=\frac{n^4+2n^3+n^2}{4}$
Por tanto ${\bar{A}}_0^x\left(n\right)=x^4\left[\frac{1}{4}+\frac{1}{2n}+\frac{1}{4n^2}\right]$
Por ejemplo, si x=3 y n=6 se tiene:
${\bar{A\ }}_0^3\left(6\right)=3^4\left[\frac{1}{4}+\frac{1}{2(6)}+\frac{1}{4{(6)}^2}\right]=81\left[\frac{1}{4}+\frac{1}{12}+\frac{1}{144}\right]=27.5625$
Por tanto ${\bar{A}\ }_0^3\left(6\right)=27.5625$
Para $f(x)=x^3$, con n el número de rectángulos inferiores, partición de x=0 a x, se tiene:
Base de todos los rectángulos: $\frac{x}{n}$
Altura del rectángulo $i$: $f\left(x_i\right)=f\left((i-1)\cdot\frac{x}{n}\right)={(i-1)\cdot\frac{x}{n})}^3$
donde $x_i=i\cdot\frac{x}{n}$ con $ con \ i=1,\ 2,\ 3,\ \ldots\ ,n$
El área aproximada ${\underline{A}\ }_0^x\left(n\right)$ es:
${\underline{A}\ }_0^x\left(n\right)=\left(\frac{x}{n}\right)\left[f(1\cdot\frac{x}{n})\right]+\left(\frac{x}{n}\right)\left[f(2\cdot\frac{x}{n})\right]+\left(\frac{x}{n}\right)\left[f(3\cdot\frac{x}{n})\right]+\ \cdot\ \cdot\ \cdot +\left(\frac{x}{n}\right)\left[f\left((n-1)\cdot\frac{x}{n}\right)\right] =\left(\frac{x}{n}\right)\left(1\cdot\frac{x}{n}\right)^3\ +\left(\frac{x}{n}\right)\left(2\cdot\frac{x}{n}\right)^3+\left(\frac{x}{n}\right)\left(3\cdot\frac{x}{n}\right)^3+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right)\left((n-1)\cdot\frac{x}{n}\right)^3 =\left(\frac{x}{n}\right)1^3\left(\frac{x}{n}\right)^3\ +\left(\frac{x}{n}\right)2^3\left(\frac{x}{n}\right)^3+\left(\frac{x}{n}\right)3^3\left(\frac{x}{n}\right)^3+\ \cdot\ \cdot\ \cdot\ +\left(\frac{x}{n}\right){(n-1)}^3\left(\frac{x}{n}\right)^3$
$=\left(\frac{x}{n}\right)^4\left[1^3+2^3+3^3+\ \cdot\ \cdot\ \cdot\ +{(n-1)}^3\right]=\frac{x^4}{n^4}\left[\frac{n^4-2n^3+n^2}{4}\right] =x^4\left[\frac{n^4-2n^3+n^2}{4n^4}\right]=x^4\left[\frac{1}{4}-\frac{1}{2n}+\frac{1}{4n^2}\right]$
Se utiliza la fórmula $1^3+2^3+3^3+\ldots+(n{-1)}^3=\left[\frac{n(n-1)}{2}\right]^2=\frac{n^4-2n^3+n^2}{4}$
Por tanto ${4{(6)}^2}\right]=81\left[\frac{1}{4}-\frac{1}{12}+\frac{1}{144}\right]=\frac{81}{4}-\frac{81}{12}+\frac{81}{400} =14.0625$
El área exacta A se encuentra entre los siguientes valores:
${\underline{A}\ }_0^3(6))\le A\le\ \ {\bar{A}}_0^3\left(6\right)$
$14.0625\le A\le\ 27.5625$
Área exacta A(x):
${\underline{A}}_0^x\left(n\right)\le A(x)\le\ \ {\bar{A}}_0^x\left(n\right)$
$\lim_{n \to \infty}\underline{A}\; _{0}^{x}(n)\le A(x)\le\lim_{n \to \infty}\bar{A_{0}^{x}}(n))$
Donde:
Área superior: ${\bar{A}\ }_0^x\left(n\right)=x^4\left[\frac{1}{4}+\frac{1}{2n}+\frac{1}{4n^2}\right]$
Área inferior: ${\underline{A}\ }_0^x\left(n\right)=x^4\left[\frac{1}{4}-\frac{1}{2n}+\frac{1}{4n^2}\right]$
$\lim_{n \to \infty}{\bar{A}}_0^4\;(n)=\lim_{n \to \infty}\left[x^4\left[\frac{1}{4}+\frac{1}{2n}+\frac{1}{4n^2}\right]\right]=\lim_{n \to \infty}x^4\left[\frac{1}{4}+\frac{1}{2}\left(\frac{1}{n}\right)+\frac{1}{4}\left(\frac{1}{n^2}\right)\right]=x^4\left[\frac{1}{4}+\frac{1}{2}\left(0\right)+\frac{1}{4}\left(0\right)\right]=\frac{1}{4}x^4$
$\lim_{n \to \infty}\underline{A}\; _{0}^{4}(n)=\lim_{n \to \infty}\left[x^4\left[\frac{1}{4}-\frac{1}{2n}+\frac{1}{4n^2}\right]\right]=\lim_{n \to \infty}x^4\left[\frac{1}{4}-\frac{1}{2}\left(\frac{1}{n}\right)+\frac{1}{4}\left(\frac{1}{n^2}\right)\right]=x^4\left[\frac{1}{4}-\frac{1}{2}\left(0\right)+\frac{1}{4}\left(0\right)\right]=\frac{1}{4}x^4$
Con lo que se tiene:
$\frac{1}{4}x^4\le A(x)\le\ \ \frac{1}{4}x^4$
Por tanto, el área exacta para la función $f(x)=x^3$ de x=0 a x es:
Función Área: $A(x)=\frac{1}{4}x^4$
El área exacta $A_2^6$ bajo la gráfica de la función $f(x)=x3$ de x=2 a x=6, ver figura, se puede obtener de la siguiente manera:
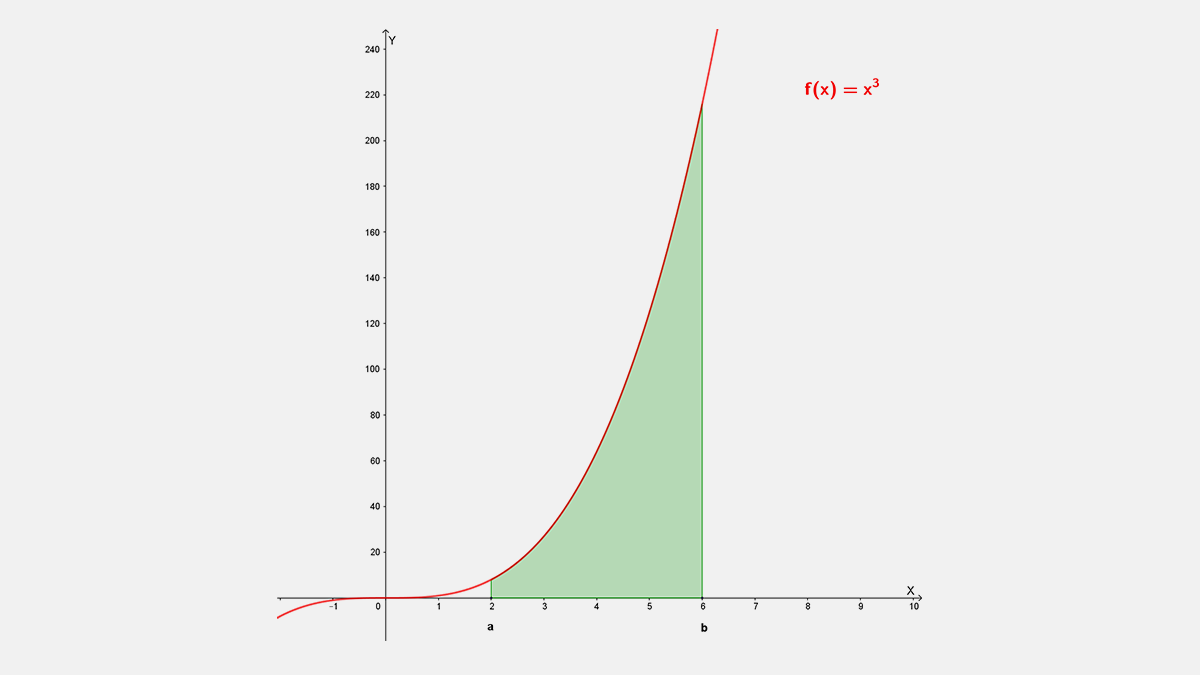
Como el área de x=0 a x está dada por la función área $A(x)=\frac{1}{4}x^4$
Si x=2 el área exacta de x=0 a x=2 es Área $A(2)=\frac{1}{4}{(2)}^4=\frac{16}{4}=4$
Si x=6 el área exacta de x=0 a x=6 es Área $A(6)=\frac{1}{4}{(6)}^4=\frac{1296}{4}=324$ aprox.
Por lo que el área exacta de x=2 a x=6 es:
$A_2^6\ =A\left ( 6 \right )-A\left ( 2 \right )=324-4=320$
En general para calcular el área exacta bajo la gráfica de la función $f(x)=x^3$ de x=a a x=b, se obtiene con la Función Área $A(x)= \frac{1}{4}x^4$ como:
${A\ }_a^b= A(x)]ab =A(b)-A(a)=\frac{1}{4}b^4-\frac{1}{4}a^4 $