Se aplica el Teorema para determinar las áreas acotadas con funciones que pueden tener valores positivos o negativos, tomando en cuenta que para funciones positivas y continuas en un intervalo, el valor de la integral Definida es directamente el área; mientras que para funciones negativas en un intervalo, el área es el valor negativo de la integral:
Para funciones continuas positivas en el intervalo [a, b], el área A entre la gráfica de la función en el intervalo y el eje X es:
$A=\ \int_{a}^{b}{f(x)dx}$
Para funciones continuas negativas en el intervalo [a, b], el área A entre la gráfica de la función en el intervalo y el eje X es:
$A=\ -\int_{a}^{b}{f(x)dx}$
El área bajo la gráfica de la función $f(x)= 2x+5$ y el eje “x”, de x=2 a x=5, mostrada en la figura, se calcula geométricamente y con el Teorema Fundamental del Cálculo, para verificar que se obtienen los mismos resultados.
La figura es un trapecio que se compone de un rectángulo de base 5-2=3 y altura 9, y un triángulo de base 5-2=3 y altura 15-9=6
Área del rectángulo: $(base)(altura)=(3)(9)=27$
Área del triángulo: $\frac{(base)(altura)}{2}=\frac{(3)(6)}{2}=9$
Área total: $A_a^b =27+9=36$
Como la función es positiva en el intervalo [2, 5], se puede calcular directamente con el Teorema Fundamental del Cálculo como sigue:
$A_a^b=\int_{a}^{b}{f(x)dx}=F(b)-F(a)$, donde $F^'(x)=f(x)$
con la función $f(x)=2x+5$ y su antiderivada $F(x)=x^2+5x$, con a=2 y b=5, se tiene que:
$〖F(5)=(5)〗^2+5(5)=25+25=50$
$〖F(2)=(2)〗^2+5(2)=4+10=14$
$A_2^5=\int_{2}^{5}{f(x)dx}=F\left(5\right)-F\left(2\right)=50-14=36 $
Por lo que el área del trapecio es: $A_2^5=36$
Observa que se obtiene el mismo resultado del área del trapecio con el cálculo directo.
Para simplificar lo anterior, la Integral Definida se puede escribir como sigue:
$A_a^b=\int_{a}^{b}{f(x)dx}=\left. F(x)\right]_a^b=F\left(b\right)-F\left(a\right) , donde F^\prime\left(x\right)=f(x)$
con la función $f\left(x\right)=2x+5$ y su antiderivada $F\left(x\right)=x^2+5x$, 𝑎=2 y 𝑏=5 se tiene:
$A_2^5=\int_{2}^{5}{(2x+5)dx}=\left. x^2+5x\right]_2^5=\left[\left. {(5)}^2+5(5)\right]\right]-\left[\left. {(2)}^2+5(2)\right]\right]=\ 50-14=36$
Por lo que el área es: $A_2^5=36$
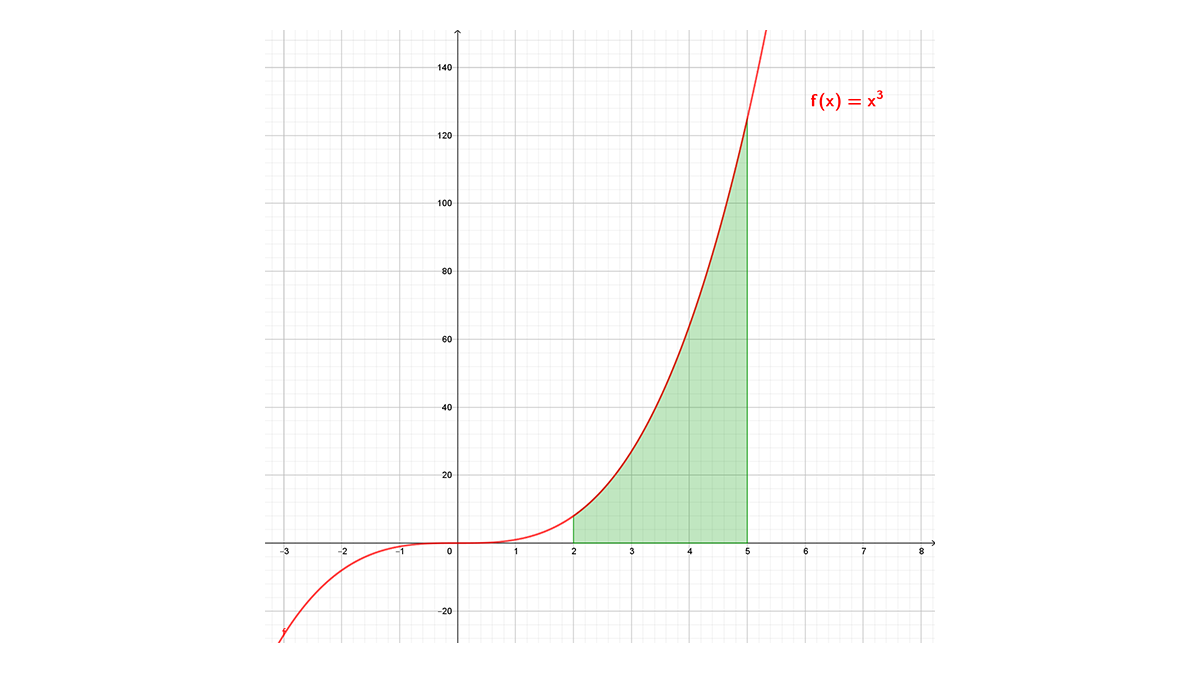
No se tiene una fórmula de la geometría elemental para calcularla como en el caso anterior, pero se puede determinar con el Teorema Fundamental del Cálculo como sigue
\int_{a}^{b}{f(x)dx}=F(b)-F(a) , donde F^\prime\left(x\right)=f(x), donde $F^' (x)=f(x)$
La función $f(x){=x}^3\ $ es positiva en el intervalo [2, 5] y su antiderivada $F\left(x\right)={\frac{1}{4}x}^4$, con $a=2$ y $b=5$
$F\left(5\right)={\frac{1}{4}(5)}^4=\frac{1}{4}(625)=\frac{625}{4}$
$F\left(2\right)={\frac{1}{4}(2)}^4=\frac{1}{4}(16)=4$
Sustituyendo estos valores en el Teorema, se tiene:
$\int_{2}^{5}{f(x)dx}=F\left(5\right)-F\left(2\right)=\frac{625}{4}-4=152.25$
Por lo que el área es: $A_2^5=\int_{2}^{5}{f(x)dx}=152.25$
Para simplificar lo anterior, la Integral Definida se puede escribir como sigue: Como la función es positiva en el intervalo, el área es el valor de la integral:
$A_a^b=\int_{a}^{b}{f(x)dx}=\left. F(x)\right]_a^b=F\left(b\right)-F\left(a\right) , donde F^\prime\left(x\right)=f(x)$
con la función $f(x){=x}^3$ y su antiderivada $F\left(x\right)={\frac{1}{4}x}^4$, $a=2$ y $b=5$ se tiene:
$A_2^5=\int_{2}^{5}{(x^3)dx}=\left.\frac{1}{4}x^4\right]_2^5=\left[\frac{1}{4}({5)}^4\right]-\left[\frac{1}{4}\left(2\right)^4\right]=\ \frac{625}{4}-\frac{16}{4}=152.25$
Por lo que el área es: $A_2^5=152.25$
Con el Teorema Fundamental del Cálculo
$A_a^b=\int_{a}^{b}{f(x)dx}=F(b)-F(a) , donde F^\prime\left(x\right)=f(x)$
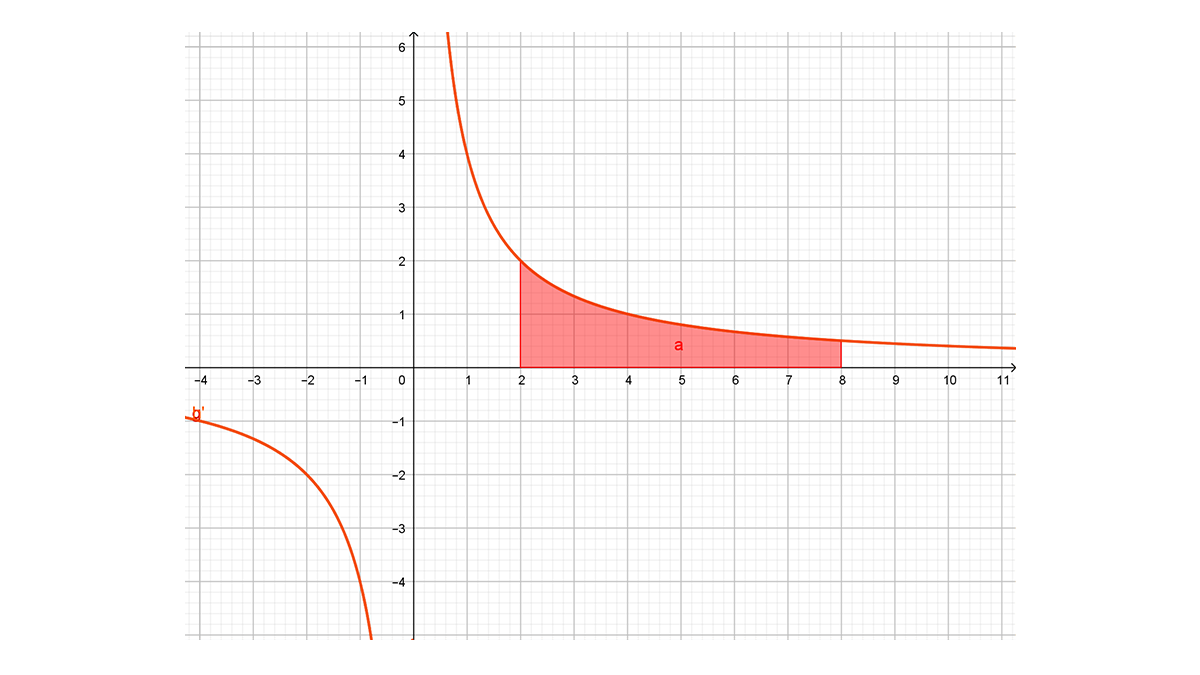
El área de se obtiene como sigue:
La función es $f(x)=\ \frac{4}{x}$ y su antiderivada $F(x)=4\ln(x))$, con $a=2$ y $b=8$
$F\left(8\right)=4\ln{\left(8\right)}=4\left(2.079\right)=8.316$
$F\left(2\right)=4\ln{\left(2\right)}=4\left(0.693\right)=2.77$
Sustituyendo estos valores en el Teorema, se tiene:
$A_2^8=\int_{2}^{8}{f(x)dx}=F\left(8\right)-F\left(2\right)=8.316-2.77=5.546$
Por lo que el área es: $A_2^8=5.546$
Para simplificar, la Integral Definida se puede escribir como sigue:
$A_a^b=\int_{a}^{b}{f(x)dx}=\left. F(x)\right]_a^b$, donde $F^\prime\left(x\right)=f(x)$ y $\left. F(x)\right]_a^b=F\left(b\right)-F\left(a\right)$
Por lo que el área es: $A_2^8=5.546$
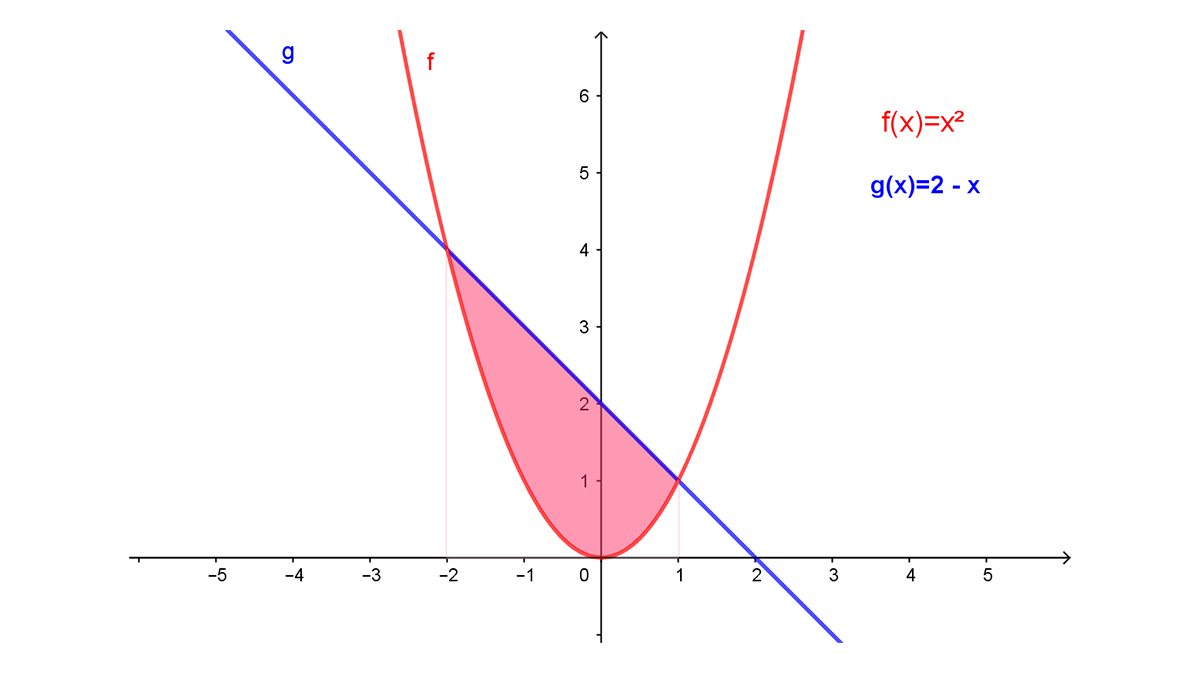
Para determinar el área señalada en la figura con el Teorema Fundamental se tiene que saber los límites de integración inferior a y superior b, es decir, determinar el intervalo de integración [a, b]. Este se puede determinar con los puntos de intersección de las dos funciones $〖f(x)=x〗^2$ y $g(x)=2-x$, igualando éstas y resolviendo la ecuación resultante:
$f\left(x\right)=g(x)\\ x^2=2-x\\ x^2+x-2=0\\ \left(x-1\right)\left(x+2\right)=0 $
solución: $x=-2$ y $x=1$
Por tanto $a=-2$ y $b=1$ y el intervalo de integración es $[a,b]=[-2,1]$
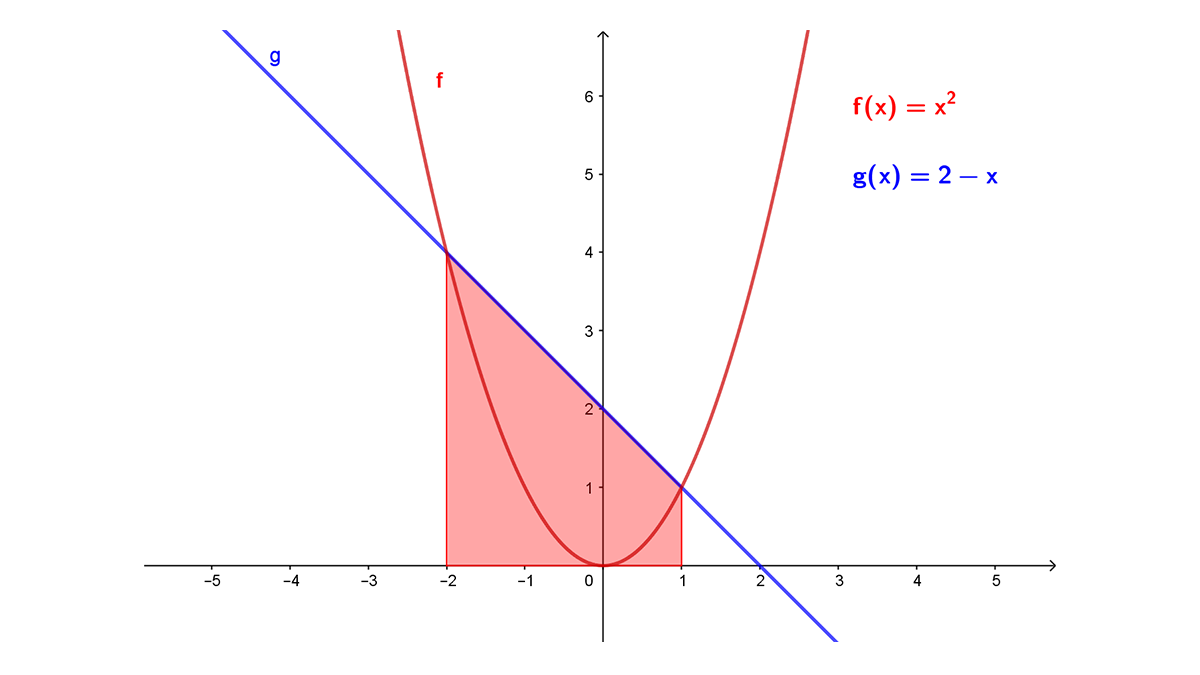
El área solicitada $A_(-2)^1$ (Fig. 1), es el área $A_1$ bajo la gráfica de $g\left(x\right)=2-x$ (Fig. 2) menos el área $A_2$ bajo la gráfica de la función $f(x)=x^2$ (Fig. 3) en el intervalo [-2, 1] , ya que la función $g(x)$ es mayor que la función $f(x)$ en el intervalo y $A_{-2}^{\ 1}=A_1-A_2$:
El área $A_1$ bajo la gráfica de $ g\left(x\right)=2+x$ con antiderivada $G\left(x\right)=2x+{\frac{1}{2}x^2}$ es
$A_1=\int_{a}^{b}{g(x)dx}=\left. G(x)\right]_a^b=G(b)-G(a)$, donde $G^\prime\left(x\right)=g(x)\\$, y a=-2, \b\ b=1
$A_1=\int_{-2}^{1}{(2-x)dx}=\left. 2x-\frac{1}{2}x^2\right]_{-2}^1=\ \left[2\left(1\right)-\frac{1}{2}{(1)}^2\right]-\left[2\left(-2\right)-{\frac{1}{2}\left(-2\right)}^2\right]=\left[\frac{3}{2}\right]-\left[-6\right]=7.5$
El área $A_2$ bajo la gráfica $f\left(x\right)=x^2$ con antiderivada $F\left(x\right)=\frac{1}{3}x^3$ es
$A_2=\int_{a}^{b}{f(x)dx}=\left. F(x)\right]_a^b=F(b)-F(a)$, donde $F^' (x)=f(x)$, a=-2 y b=1
$A_2=\int_{-2}^{1}{(x^2)dx}=\left. \frac{1}{3}x^3\right]_{-2}^1=\ \left[\frac{1}{3}{(1)}^3\right]-\left[\frac{1}{3}{(-2)}^3\right]=\left[\frac{1}{3}\right]-\left[\frac{-8}{3}\right]=3\ \$
El área $A_{-2}^{\ 1}$ entre las gráficas $g\left(x\right)=2+x$ y $f\left(x\right)=x^2$ es
$A_{-2}^{\ 1}=A_1-A_2=7.5-3=\mathbf{4}.\mathbf{5}$
Por lo que el área solicitada es: 4.5
Otro procedimiento:
Como $g\left(x\right)=2-x$ es mayor que $f(x)=\ x^2$ en el intervalo [-2. 1]
El área solicitada se puede calcular con la integral de la función
$g(x)-f(x)=(2-x)-〖(x〗^2)=2-x-x^2$
$A_{-2}^{\ 1}=\int_{-2}^{1}\left[g\left(x\right)-f(x)\right]dx=\ \int_{-2}^{1}\left[2-x-x^2\right]dx=\left. 2x-\frac{1}{2}x^2-\frac{1}{3}x^3\right]_{-2}^1\ =\left[2\left(1\right)-\frac{1}{2}\left(1\right)^2-\frac{1}{3}\left(1\right)^3\right]-\left[2\left(-2\right)-\frac{1}{2}\left(-2\right)^2-\frac{1}{3}\left(-2\right)^3\right]=\left[\frac{7}{6}\right]-\left[\frac{-10}{3}\right]=\frac{27}{6}=4.5$
Por lo que el área es: $A_{-2}^{\ 1}==4.5$
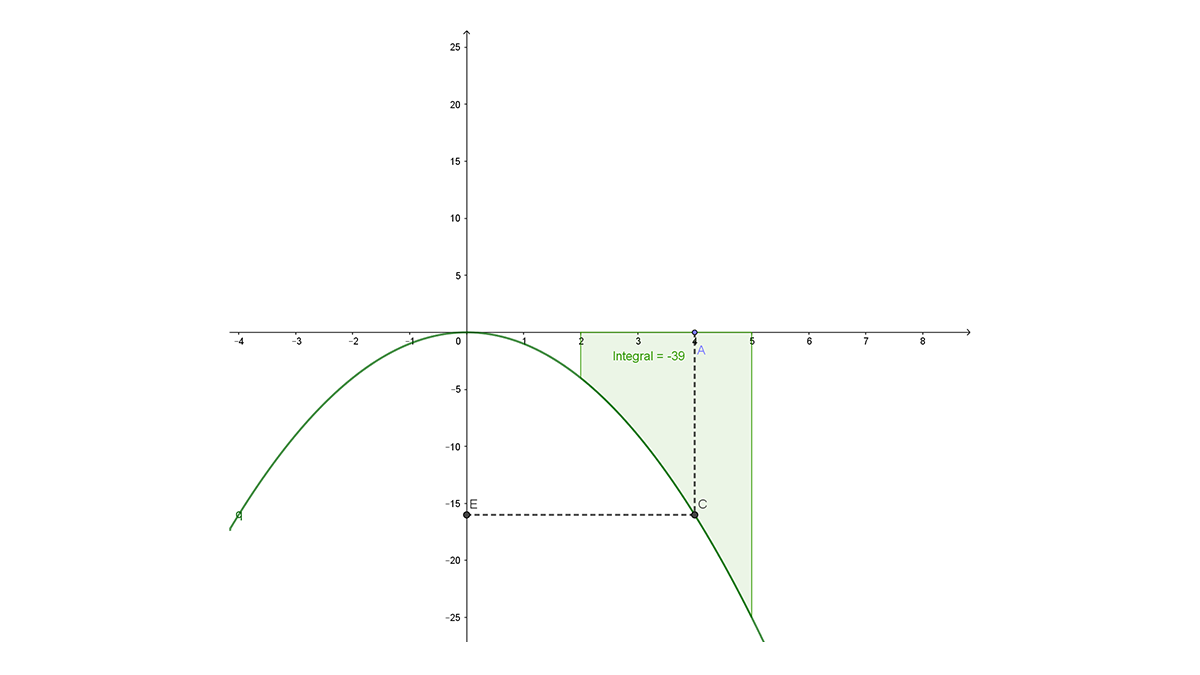
• El área entre la gráfica de la función $f\left(x\right)=-x^2$ y el eje X de x=2 a x=5 con la Integral Definida (Fig.2), se puede calcular como sigue, para repasar el uso de la integral:
• El área entre la gráfica de la función $f\left(x\right)=x^2$ y el eje X de x=2 a x=5 con la Integral Definida (Fig.1), se puede calcular como sigue:
La integral definida de la función f(x) de x=2 a x=5 es:
$\int_{2}^{5}{\left(x^2\right)dx=}\left. \frac{1}{3}x^3\right]_2^5=\left[\frac{1}{3}{(5)}^3\right]-\left[\frac{1}{3}\left(2\right)^3\right]=\frac{125}{3}-\frac{8}{3}=\frac{117}{3}=39$
Como la función f(x) es positiva en el intervalo, la integral es positiva y el área es el valor de la integral:
$A_2^5=\int_{2}^{5}{\left(x^2\right)dx=}39$
Por tanto, el área solicitada Fig. 1 es $A_2^5=39$
• El área entre la gráfica de la función f(x)=〖-x〗^2 y el eje X de x=2 a x=5 con la Integral Definida (Fig.2), se puede calcular como sigue:
La integral definida de la función f(x)=〖-x〗^2 de x=2 a x=5 es:
$\int_{2}^{5}{\left({-x}^2\right)dx=}{-\left. \frac{1}{3}x^3\right]}_2^5=\left[-\frac{1}{3}{(5)}^3\right]-\left[-\frac{1}{3}\left(2\right)^3\right]=-\frac{125}{3}+\frac{8}{3}=\frac{117}{3}=-39$
Observa que como la función es negativa en el intervalo [2, 5] la integral tiene un valor negativo y no representa el área requerida, ya que no debe ser negativa.
Para calcular el área cuando la función es negativa en el intervalo, se toma el valor negativo de la integral, esto es,
$A_2^5=-\int_{2}^{5}{\left({-x}^2\right)dx=-\left(-39\right)=39}$
Por tanto, el área solicitada Fig. 2 es $A_2^5=39$
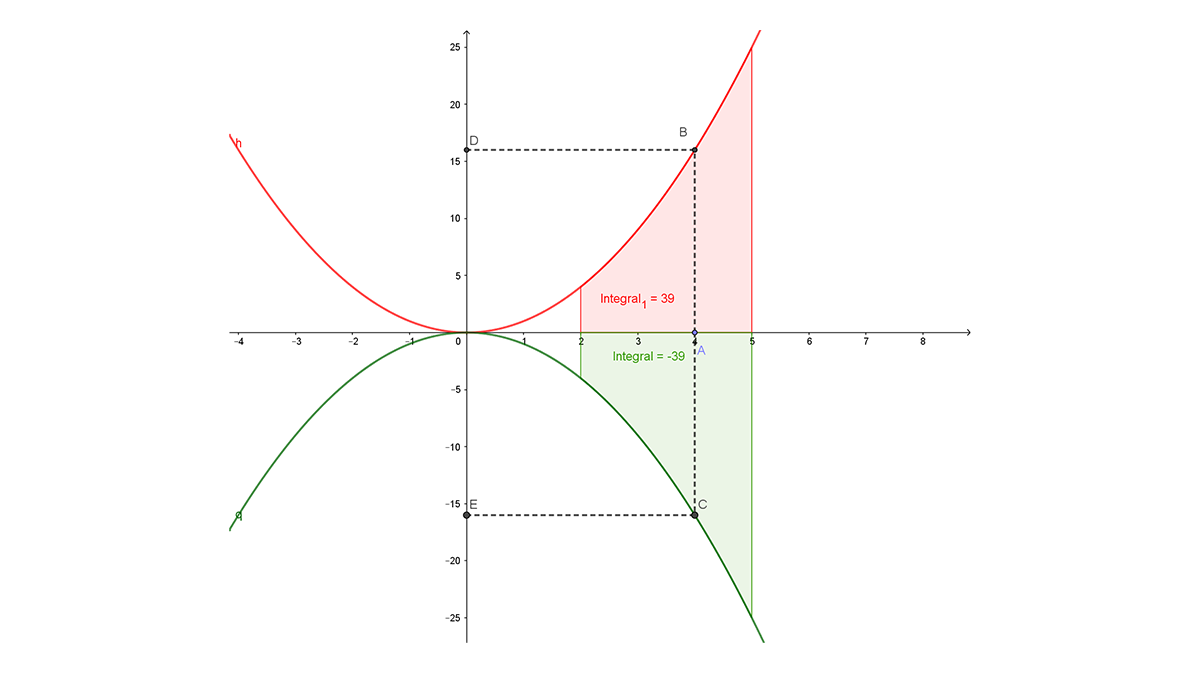
En la Fig. 3 se observa que las áreas, roja para la función $f\left(x\right)=x^2$ (Fig.1) y azul para la función $f(x)=〖-x〗^2$ (Fig.2) son iguales, aunque las integrales tienen signos diferentes.
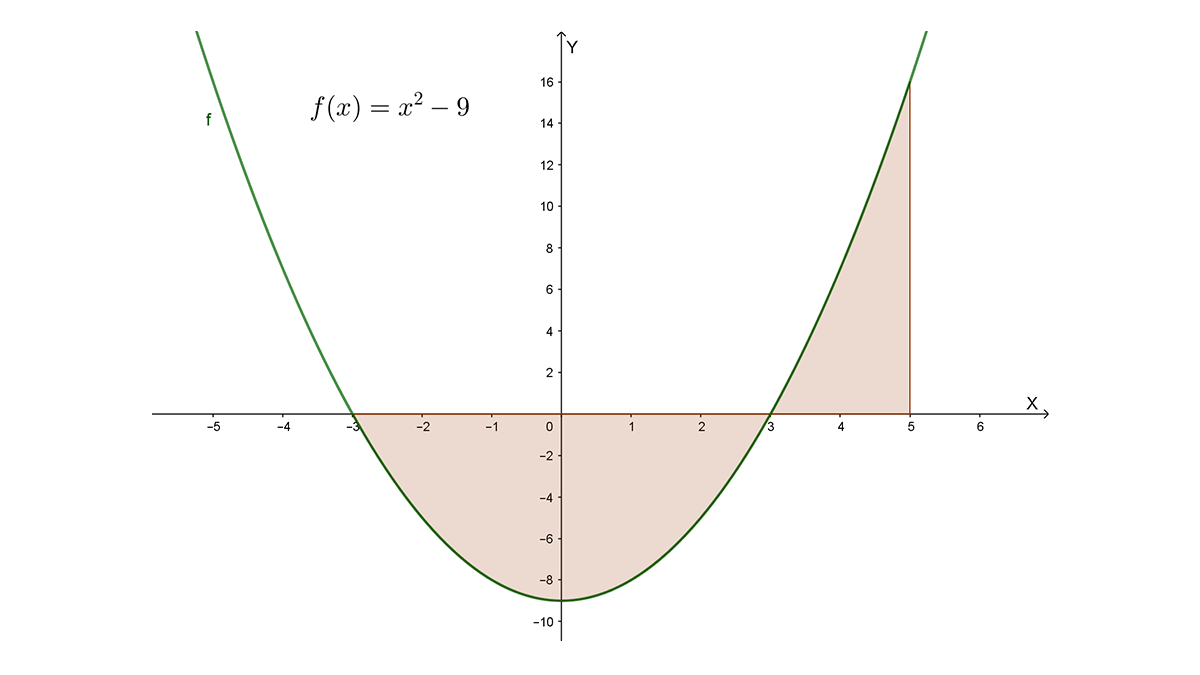
Con la Integral Definida se puede calcular como sigue:
Como el área solicitada A, tiene una parte área A1 con la función negativa en el intervalo [-3, 3] y una parte área A2 con la función positiva en el intervalo [3, 5], se calculan por separado con la integral definida y después se suman: A=A1+A2
La integral definida en el intervalo [-3, 3] es
$\int_{-3}^{3}{f\left(x\right)dx=\int_{-3}^{3}{{(x}^2-9\ )dx}=\left. \frac{1}{3}x^3-9x\right]_{-3}^3}=\left[\frac{1}{3}{(3)}^3-9(3)\right]-\left[{\frac{1}{3}\left(-3\right)}^3-9\left(-3\right)\right]=\left[9-27)\right]-\left[-9+27\right]=\left[-18)\right]-\left[18\right]=-36$
Como la función es negativa en el intervalo [-3, 3], el valor de la integral es negativa y por tanto el área A1 es
$\int_{3}^{5}{f\left(x\right)dx=\int_{3}^{5}{{(x}^2-9\ )dx}=\left. \frac{1}{3}x^3-9x\right]_3^5}=\left[{\frac{1}{3}\left(5\right)}^3-9(5)\right]-\left[{\frac{1}{3}\left(3\right)}^3-9\left(3\right)\right]=\left[\frac{125}{3}-45\right]-\left[9-27\right]=\left[-\frac{10}{3}\right]-\left[-18\right]=\frac{44}{3}$
Como la función es positiva en el intervalo [3, 5], el valor de la integral es positiva y el área A22 es
$A1=\ -\int_{-3}^{3}{f\left(x\right)dx=-(-36)=36}$
La integral definida en el intervalo [3, 5] es
$\int_{3}^{5}{f\left(x\right)dx=\int_{3}^{5}{{(x}^2-9\ )dx}=\left. \frac{1}{3}x^3-9x\right]_3^5}=\left[{\frac{1}{3}\left(5\right)}^3-9(5)\right]-\left[{\frac{1}{3}\left(3\right)}^3-9\left(3\right)\right]=\left[\frac{125}{3}-45\right]-\left[9-27\right]=\left[-\frac{10}{3}\right]-\left[-18\right]=\frac{44}{3}$
Como la función es positiva en el intervalo [3, 5], el valor de la integral es positiva y el área A22 es
$\int_{3}^{5}{f\left(x\right)dx=\frac{44}{3}}=14.666\ldots$
Por lo que el área solicitada es A=A1+A2=36+14.666…=50.666…
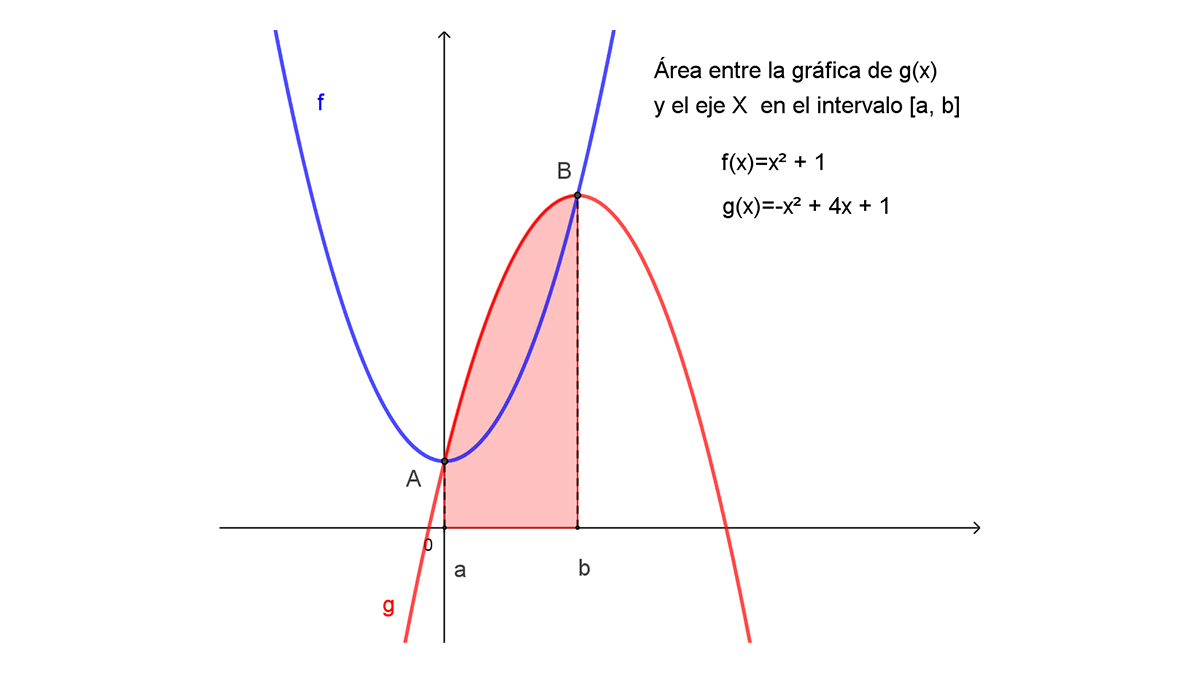
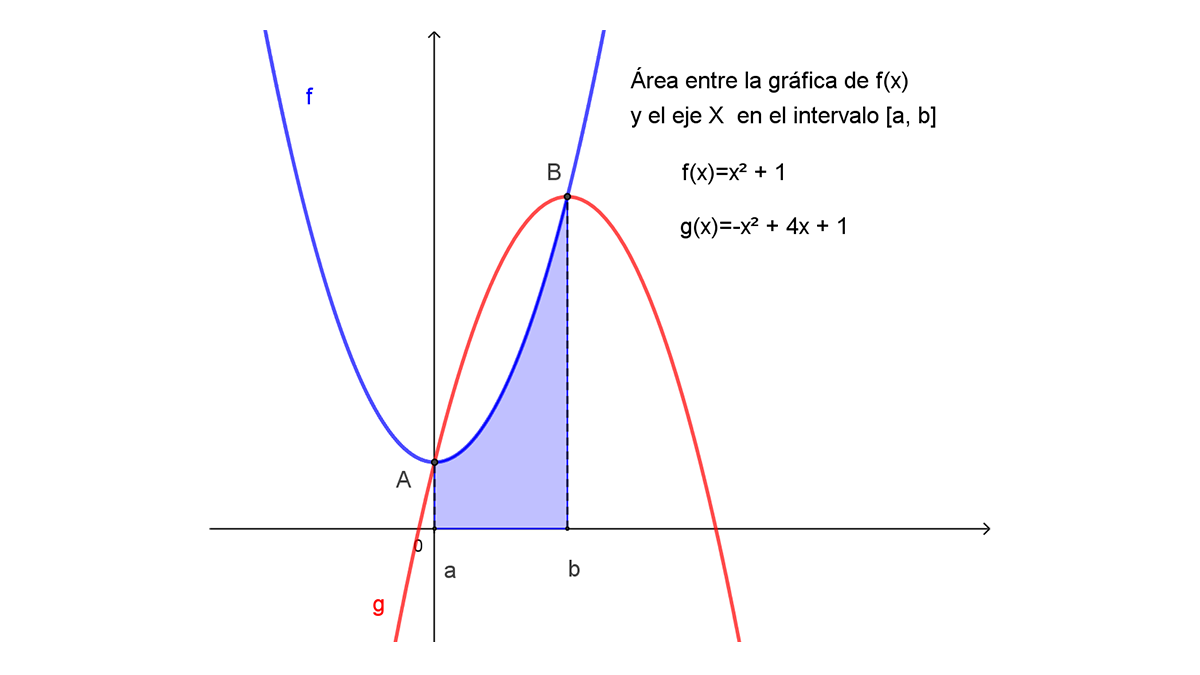
Para determinar el área señalada en la figura con el Teorema Fundamental se tiene que saber los límites de integración inferior a y superior b, es decir, determinar el intervalo de integración [a, b]. Este se puede determinar con los puntos de intersección de las dos funciones ${f(x)=x}^2+1 \quad y\quad g\left(x\right)={-x}^2+4x+1$, igualando éstas y resolviendo la ecuación resultante:
$f\left(x\right)=g(x)$
$x^2+1={-x}^2+4x+1$
$2x^2-4x=0$
$\left(2x)(x-2\right)=0$ solución: x=0 y x=2
Por tanto a=0 y b=2 y el intervalo de integración es $\left[a,\ b\right]=[0,\ 2]$
El área solicitada $A_0^2$ (Fig. 7.1), es el área A_1 bajo la gráfica de $g\left(x\right)={-x}^2+4x+1$ (Fig. 7.2) menos el área $A_2$ bajo la gráfica de la función $f\left(x\right)=x^2+1$ (Fig. 7.3) en el intervalo [0,2] , ya que la función $g(x)$ es mayor que la función $f(x)$ en el intervalo y $A_0^{\ 2}=A_1-A_2$:
El área $A_1$ bajo la gráfica de $g\left(x\right)={-x}^2+4x+1$ con antiderivada $G\left(x\right)=-{\frac{1}{3}x}^3+2x^2+x$ es $A_1=\int_{a}^{b}{g(x)dx}=\left. G(x)\right]_a^b=G(b)-G(a)$, donde $G^\prime\left(x\right)=g(x), \quad a=-2 \quad y\quad b=1$
$A_1=\int_{0}^{2}{({-x}^2+4x+1\ \ )dx}=\left. -{\frac{1}{3}x}^3+2x^2+x\ \ \right]_0^2=\ \left[-{\frac{1}{3}(2)}^3+2{(2)}^2+2\ \ \right]-\left[-{\frac{1}{3}\left(0\right)}^3+2\left(0\right)^2+0\ \ \right]=\left[-\frac{8}{3}+10\right]-\left[0\right]=\frac{22}{3}$
El área $A_2$ bajo la gráfica $f\left(x\right)=x^2+1$ con antiderivada $G\left(x\right)=-{\frac{1}{3}x}^3+2x^2+x$ es
$A_1=\int_{a}^{b}{f(x)dx}=\left. F(x)\right]_a^b=F(b)-F(a)\ ,\ donde\ F^\prime\left(x\right)=f(x)\ ,\ a=0\ \ y\ \ \ b=2$
Se tiene que $A_0^2=A_1+A_2=\frac{22}{3}-\frac{14}{3}=\frac{8}{3}$
Por lo que el área solicitada es: $A_0^{\ 2}=\frac{8}{3}$
Otro procedimiento:
Como $g\left(x\right)={-x}^2+4x+1$ es mayor que $f\left(x\right)=x^2+1$ en el intervalo [0,2]
El área solicitada se puede calcular con la integral de la función
$g\left(x\right)-f\left(x\right)=\left({-x}^2+4x+1\right)-{(x}^2+1)=-{2x}^2+4x$
$A_0^{\ 2}=\int_{0}^{2}\left[g\left(x\right)-f(x)\right]dx=\ \int_{0}^{2}\left[-{2x}^2+4x\right]dx=\left. -\frac{2}{3}x^3+2x^2\right]_0^2\ =\left[-\frac{2}{3}{(2)}^3+2{(2)}^2\right]-\left[-\frac{2}{3}\left(0\right)^3+2\left(0\right)^2\right]=\left[-\frac{16}{3}+8\right]-\left[0\right]=\frac{8}{3}$
Por lo que el área solicitada es: $A_0^{\ 2}=\frac{8}{3}$