Función f(x) y Función Área A(x)
La tabla siguiente concentra la relación de la función f(x) y la Función Área A(x) de x=0 a x , para las funciones originales f(x) tratadas en las actividades anteriores.
| Función Original | Función Área |
|---|---|
| $v(t)=10t$ | $A(t)=5t^2$ |
| $〖f(x)=x〗^2$ | ${A(x)=\frac{1}{3}x}^3$ |
| $〖f(x)=x〗^3$ | ${A(x)=\frac{1}{4}x}^4$ |
La Función Área A(x) se obtuvo como el límite de las sumas de rectángulos superiores A ̅_0^x (n) e inferiores ▁A_0^x (n), donde los límites son iguales, cuando el número n de rectángulos de igual base x/n tiende a infinito y la base de los rectángulos tiende a cero:
$A(x)= \lim_{n \to \infty}{\bar{A}}_0^x\left(n\right)=\lim_{n \to \infty}{\underline{A}\ }_0^x(n)$
Función Área A(x) y la Integral Definida $\int_{a}^{b}f\left(x\right)dx$
La Función Área A(x) para la función original f(x) positiva en el intervalo de x=0 a x , se identifica con la denominada Integral de la función f(x) y la denotamos por:
$A(x)=\int_{0}^{x}{f(x)dx}$
El área A_a^b bajo la gráfica de la función f(x) positiva en el intervalo de x=a a x=b, se obtuvo con la función área A(x) como:
$A_a^b\ =\ A(b)\ – A(a) $
o con la denominada Integral Definida de la función f(x) como:
$\int_{0}^{x}{f(x)dx}=A_a^b=A(b)-A(a)$, donde A(x) es una antiderivada de f(x), a es límite inferior y b el límite superior de la Integral Definida.
Integral Definida de una función
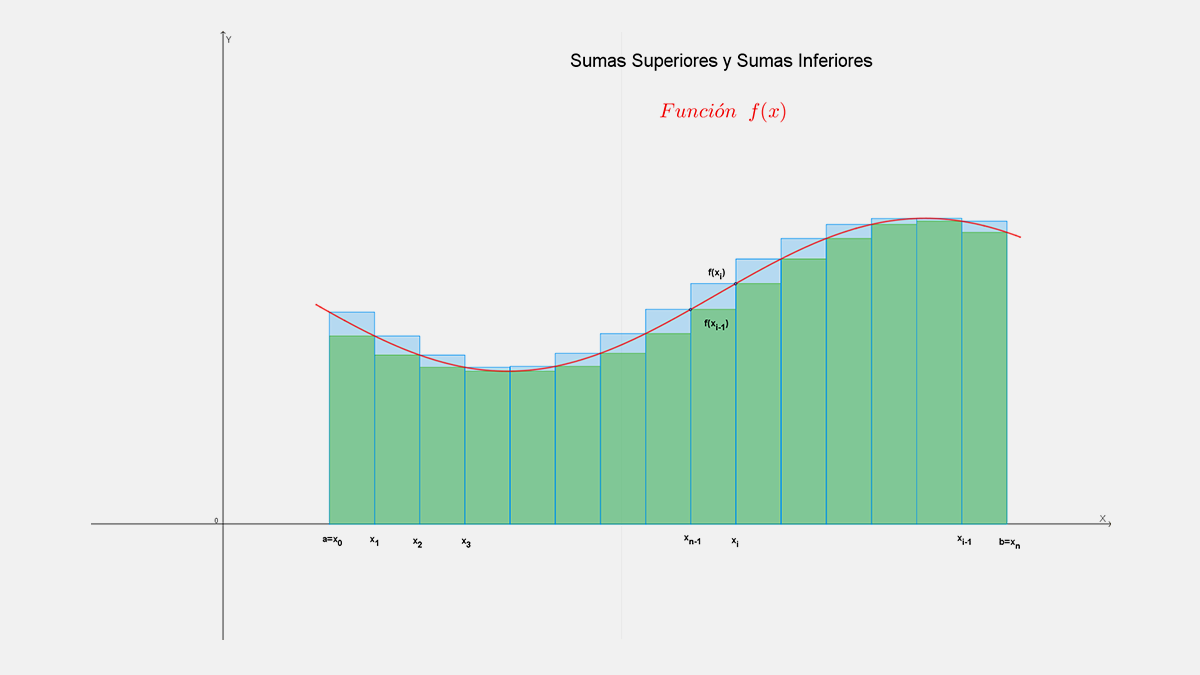
En las actividades anteriores, para facilitar los cálculos, se determinó el Área exacta de x=0 a x y la Función Área para algunas funciones no negativas, crecientes con el límite de las aproximaciones de las sumas superiores e inferiores del área de n rectángulos, cuando n tiende a infinito y con iguales intervalos para las bases x/n que tienden a cero, donde el valor menor de la función se encuentra al inicio de cada subintervalo y el valor mayor al final de éste.
Sin embargo, para cualquier función continua las aproximaciones de las sumas se pueden hacer con subintervalos de diferente tamaño para las bases de los rectángulos y donde los valores mayores y menores de la función en cada subintervalo pueden estar en cualquier punto de éste y ser positivos o negativos. El límite de las sumas superiores e inferiores se toma cuando las bases de los rectángulos tienden a cero y representa el área en el intervalo donde la función es positiva.
Para la definición de Integral Definida de una función continua en un intervalo de x=a a x=b se consideran las siguientes definiciones:
Partición de un intervalo [a, b]:
Conjunto de puntos xi con i=1, 2, 3, … ,n que dividen al intervalo [a, b] en n subintervalos de
longitud $bigtriangleup _i=x_i-x_{i-1}$, donde
${a=x}_0 Suma superior $¯S$: $\overline{S}=f\left({\overline{x}}_1\right)\Delta_{1}+f\left({\overline{x}}_2\right)\Delta_{2}+f\left({\overline{x}}_3\right)\Delta_{3}+\cdot
\cdot \cdot
+f\left({\overline{x}}_{i-1}\right)\Delta_{i-1}+f\left({\overline{x}}_i\right)\Delta_{i}+\cdot
\cdot \cdot
+f\left({\overline{x}}_{n-1}\right)\Delta_{n-1}+f\left({\overline{x}}_n\right)\Delta_{n}$
donde $\bigtriangleup _i=x_i-x_{i-1}$ es el subintervalo $i$ y $f(¯x )$ el valor
mayor de la función en el subintervalo. Suma inferior $▁S$: $\overline{S}=f\left({\underline{x}}_{\1}\right)\Delta_{1}+f\left({\underline{x}}_{\2}\right)\Delta_{2}+f\left({\underline{x}}_{\3}\right)\Delta_{3}+\cdot
\cdot
\cdot+f\left({\underline{x}}_{\i-1}\right)\Delta_{i-1}+f\left({\underline{x}}_{\i}\right)\Delta_{i}+\cdot\cdot\cdot+f\left({\underline{x}}_{n-1}\right)\Delta_{n-1}+f\left({\underline{x}}_{n}\right)\Delta_{n}$
donde $∆_i=x_i-x_(i-1)$ es el subintervalo $i$ y $f( ▁x_(i)$ el valor menor
de la función en el subintervalo.
Definición de la Integral Definida $∫_a^b▒〖f(x)dx〗$
La Integral Definida de una función continua en un intervalo [a, b], denotada como $∫_a^b▒〖f(x)dx〗$ , se define como el límite de las sumas superiores $¯S$ e inferiores $▁S$, cuando la longitud de los subintervalos ∆_i tiende a cero y los límites son iguales:
$\int_{a}^{b}{f(x)dx}=\lim_{\Delta_{i}\to\ 0}\overline{S}=\lim_{\Delta_{i}\to\ 0}\underline{S}$
Para funciones continuas positivas en el intervalo [a, b], se tiene que:
$\Delta_{i}f\left({\overline{x}}_i\right)$ es el área del rectángulo superior $i$, donde $\Delta_{i}$ es su base y $f(\ {\overline{x}}_i)$ su altura.
$\Delta_{i}f({\underline{x}\ }_i)$ es el área del rectángulo inferior $i$ donde $\Delta_{i}$ es su base y ${f(\ \underline{x}\ }_i)$ su altura.
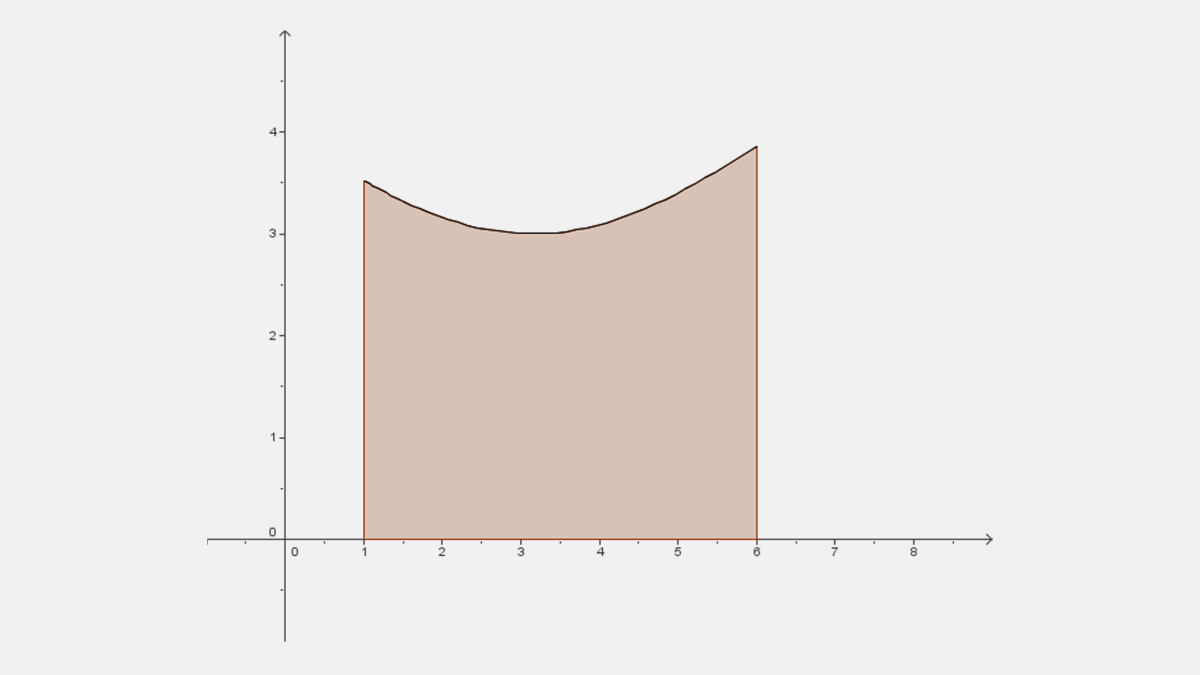
El área $A$ debajo la gráfica de la función y el eje “x” en el intervalo [a, b] es el valor la integral definida.
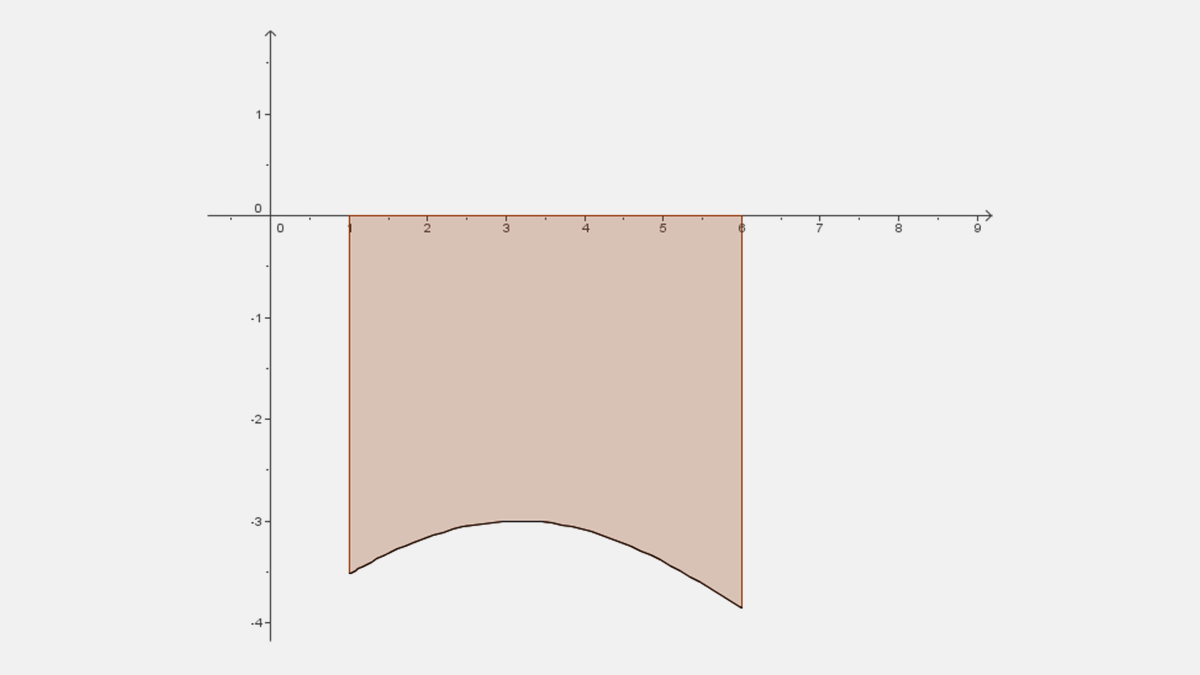
Para funciones continuas negativas en el intervalo [a, b], la altura de los rectángulos $i$ es $-f(\ {\overline{x}}_i)$ y $-f(\ {\underline{x}}_i)$, por lo que la integral es negativa. Para obtener el área se toma el valor negativo de la integral, como se verá más adelante en los ejemplos.
$A=\int_{a}^{b}{f(x)dx}$
Para funciones continuas positivas en el intervalo [a, b], el área A entre la gráfica de la función en el intervalo y el eje X es
$A= \int_{a}^{b}{f(x)dx}$
$A=-\int_{a}^{b}{f(x)dx}$
Para funciones continuas negativas en el intervalo [a, b], el área A entre la gráfica de la función en el intervalo y el eje X es
$A=-\int_{a}^{b}{f(x)dx}$
Propiedades de la Integral Definida de una función
Para funciones $f(x)$ y $g(x)$ continuas en el intervalo $[a,b]$ se tienen las siguientes propiedades:
- $\int_{a}^{b}\left[cf(x)\right]dx=c\int_{a}^{b}{f(x)dx}$, si $c$ es una constante
- $\int_{a}^{b}{f(x)dx}=\int_{a}^{c}{f(x)dx}+\int_{c}^{b}{f(x)dx}$, Si $a
- $\int_{a}^{b}\left[f\left(x\right)\pm g(x)\right]dx=\int_{a}^{b}{f(x)dx}\pm\int_{a}^{b}{g(x)dx}$
- $\int_{a}^{b}{f(x)dx}\le\int_{a}^{b}{g(x)dx} , si f(x)\le g(x)$