Solución de la forma ax2+bx=0
Para resolver esta forma se considerarán dos ecuaciones en las que se detallará el procedimiento de solución, observa que cada uno de los ejemplos responde a la forma ax2+bx=0 , da clic en cada pestaña para revisarlos:
Solución de la ecuación 5x2−20x=0
Esta ecuación tiene la estructura de la forma ax2+bx=0, ya que al sustituir los valores a=5 y b=−20 queda de la siguiente manera:
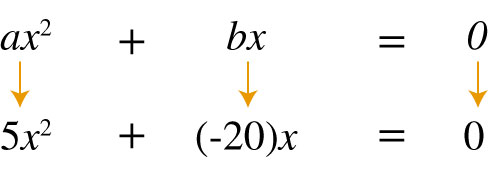
Como la suma de los términos del lado izquierdo de la ecuación es igual a cero y tienen como factor común la incógnita x, este tipo de ecuaciones pueden resolverse por medio de una factorización sencilla y utilizando la propiedad del producto nulo, es decir, la propiedad de cuando el producto de dos números es igual a cero.
Revisa el proceso dando clic en los números
5x2−20x=0
5x2−20x=0
x(5x−20)=0
Se factoriza el lado izquierdo de la ecuación, ya que x(5x−20)=5x2−20x.
5x2−20x=0
x(5x−20)=0
x=0 o 5x−20=0
Como el producto de x con 5x−20 es cero, implica que cada uno de los factores puede ser cero.
Se tiene por tanto x1=0
Solución 1, obtenida a partir de x=0.
5x2−20x=0
x(5x−20)=0
x=0 o 5x−20=0
De 5x−20=0
Resolviendo la ecuación 5x−20=0 se encuentra la segunda solución.
5x2−20x=0
x(5x−20)=0
x=0 o 5x−20=0
De 5x−20=0
5x−20+20=0+20
Con la intención de despejar la variable x, se suma 20 a cada lado de la ecuación.
5x=20
Se simplifica la ecuación.
5x2−20x=0
x(5x−20)=0
x=0 o 5x−20=0
De 5x−20=0
5x−20+20=0+20
5x=20
5x5=205
Para continuar el despeje de la variable x se divide entre 5 cada lado de la ecuación.
Se tiene por tanto x1=0
Solución 1, obtenida a partir de x=0.
Por lo tanto x2=4
Solución 2, obtenida a partir de x=4.
Comprobación
Para realizar la comprobación se sustituye cada una de las soluciones encontradas en la ecuación original y se verifica que se cumpla la igualdad:
Con x=0
5x2−20x=0
5(0)2−20(0)=0
5(0)−0=0
0−0=0
0=0
Con x=4
5x2−20x=0
5(4)2−20(4)=0
5(16)−80=0
80−80=0
0=0
Como se cumple la igualdad, las soluciones encontradas son correctas.
Una variante resumida del procedimiento anterior es la siguiente:
Se pueden hacer otras factorizaciones para resolver la ecuación 5x2−20x=0, por ejemplo:
5x2−20x=5x(x−4), por lo que la ecuación equivale a 5x(x−4).
Como el producto de los números 5x y x−4 es cero, implica que 5x=0 o x−4=0.
De 5x=0 se obtiene x=05=0 por lo que la solución 1 es x1=0.
De x−4=0 se obtiene que la solución 2 es x2=4
Estas son las mismas soluciones encontradas en el ejemplo anterior.
Solución de la ecuación 43x2−7x=0
Esta ecuación está compuesta por una fracción en el parámetro cuadrático, sin embargo, sigue presentando la misma estructura de la forma ax2+bx=0, por lo que el proceso de solución es el mismo que el anterior como se verá a continuación:
Revisa el proceso dando clic en los números
43x2−7x=0
43x2−7x=0
x(43x−7)=0
Se factoriza el lado izquierdo de la ecuación, ya que x(43x−7)=43x2−7x.
43x2−7x=0
x(43x−7)=0
x=0 o (43x−7)=0
Ya que el producto de x con 43x−7 es cero, implica que cada uno de los factores puede ser cero.
Se tiene por tanto x1=0
Solución 1, obtenida a partir de x=0.
43x2−7x=0
x(43x−7)=0
x=0 o (43x−7)=0
De 43x−7=0
Al resolver la ecuación se encuentra la otra solución.
43x2−7x=0
x(43x−7)=0
x=0 o (43x−7)=0
De 43x−7=0
43x−7+7=0+7
Sumando 7 a cada lado de la igualdad.
43x=7
Simplificando.
43x2−7x=0
x(43x−7)=0
x=0 o (43x−7)=0
De 43x−7=0
43x−7+7=0+7
43x=7
43x43=743
Dividiendo entre 43 cada lado de la ecuación.
x=214 por tanto x2=214
Simplicando, se obtiene la solución 2.
Comprobación
Para efectuar la comprobación, se sustituye cada una de las soluciones encontradas en la ecuación original 43x2−7x=0 y se verifica que se cumpla la igualdad:
Para x1=0
43x2−7x=0
43(0)2−7(0)=0
43(0)−7(0)=0
0−0=0
0=0
Para x2=214
43x2−7x=0
43(214)2−7(214)=0
43(44116)−(1474)=0
1474−1474=0
0=0
Como se cumple la igualdad, las soluciones encontradas son correctas.


