La Real Academia Española, en su quinta acepción define problema como un “planteamiento de una situación cuya respuesta desconocida debe obtenerse a través de métodos científicos”.
Un problema de cómputo, es aquel que tiene que resolverse con un lenguaje de programación, utilizando técnicas de ingeniería de software que nos ayudan a crear la abstracción (modelo) de una situación real, permitiendo automatizar un proceso mediante un programa de cómputo.
Similar al planteamiento de un problema de física o matemáticas, debe establecerse un enunciado coherente y claro que permita describir la situación que se desea resolver, identificar con qué datos se cuenta (entradas), qué se desea obtener (salidas). Permite establecer que interrelaciones existen entre la información y qué procesos son factibles de realizar con una computadora para obtener la solución (proceso).
Con este ejercicio identificarás los elementos de un sistema y el orden adecuado para resolver un problema.
En el siguiente diagrama, arrastra las leyendas que correspondan a los elementos de un sistema.
Proceso
- Entradas
Las entradas de un sistema o un programa de cómputo constituyen la información con la que cuenta el programador y que deberá proporcionar el usuario (u otro sistema). Responde a las preguntas ¿qué información tengo? o ¿con qué información de entrada puedo contar? - Proceso
El programador requiere identificar cuáles son las interrelaciones que existen entre los elementos de entrada y salida, es decir, que trabajo se tiene que llevar a cabo para obtener las salidas a partir de las entradas que se tienen. - Salidas
Las salidas del sistema son la información que se desea obtener. Por lo general es la primera pregunta que se hace al solicitante de una solución informática: ¿qué deseo obtener o solucionar?
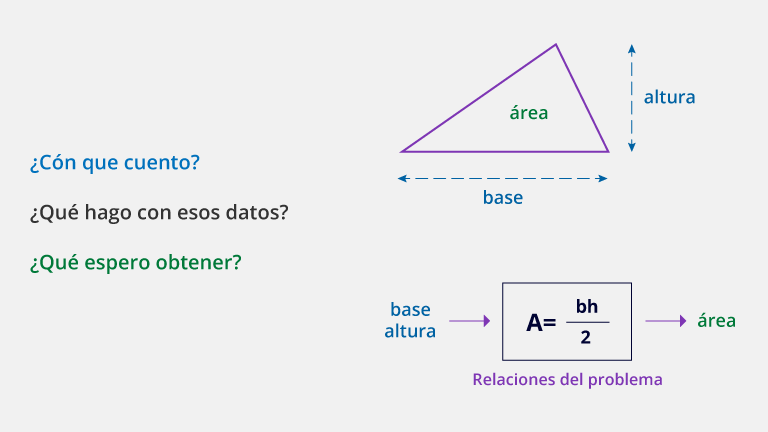
Si se desea calcular el área de un triángulo, qué información corresponde a cada uno de los elementos de un sistema.
-
Cálculo del área de un triángulo
Opciones $Área (A)$ $A=\tfrac{bh}{2}$ $Base (b) Altura (h)$ -
Calcular el índice de masa corporal de una persona, conociendo su peso y estatura. A saber, el IMC se calcula como $imc=\tfrac{peso}{estatura^2}$
Opciones $imc=\tfrac{peso}{estatura^2}$ $imc$ $peso$ $estatura$ -
Calcular las raíces $x_1$ y $x_2$ de una ecuación de segundo grado de la forma $ax^2+bx+c$.
Opciones $x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$ $x_1, x_2$ $a, b, c$