En este apartado clasificaremos los diferentes tipos de problemas que comúnmente se plantean en el área de cómputo con la finalidad de encontrar una solución o respuesta. La clasificación de este tipo de problemas utiliza ciertos criterios que a continuación explicaremos.
Un criterio se refiere a la clasificación que establece la relación entre los datos de entrada y los datos de salida o resultados, como problemas de tipo determinístico y de tipo probabilístico; otro criterio que se emplea es el tipo de proceso que se aplica a los datos para encontrar el resultado, en estos casos los problemas se clasifican como secuenciales o condicionales.
Detallemos cada uno de los tipos de problemas.
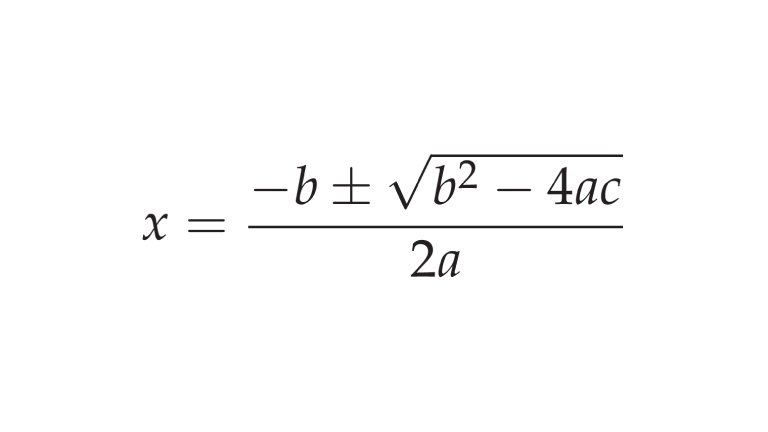
Los problemas de tipo determinístico se llaman así porque el resultado de la solución será determinado por los valores de entrada o condiciones de inicio y este resultado siempre será igual y no existirá variación alguna cuando los valores de entradas sean los mismos. Estos problemas generalmente tienen un comportamiento lineal, es decir, cada paso de la solución tiene uno anterior y uno posterior. Generalmente son problemas donde sabemos con certeza cuáles son los datos de entrada y derivado de eso sabemos qué resultado estamos esperando a la salida del proceso. La aplicación de una fórmula matemática para el cálculo del área de algún tipo de figura siempre dará el mismo resultado con los mismos valores de entrada, por ejemplo.
Los problemas probabilísticos son aquellos que tienen una solución probable que no siempre será la misma puesto que al menos una variable de los datos de entrada será tomada al azar; una solución que varía en función del proceso que se realice con los datos de entrada en donde la variable tomada al azar definirá qué camino se seguirá. Estos problemas basan su razonamiento en la probabilidad de que se presente determinada solución dada cierta condición inicial. Este tipo de variable generalmente tiene que ver en la vida real, con una percepción o un grado de creencia que asigna la probabilidad sobre la posibilidad de ocurrencia de un resultado estimado. Por ejemplo, el cálculo del pronóstico del tiempo de un día de la semana.
Cuando no encontramos un método determinístico que proporcione una solución al problema o el tiempo que se necesita es tan alto que los algoritmos son inviables, entonces deberíamos tratar de encontrar una solución aproximada o bien una solución que sea factible en un alto porcentaje. Generalmente este tipo de soluciones se basan en la aplicación de métodos estadísticos.
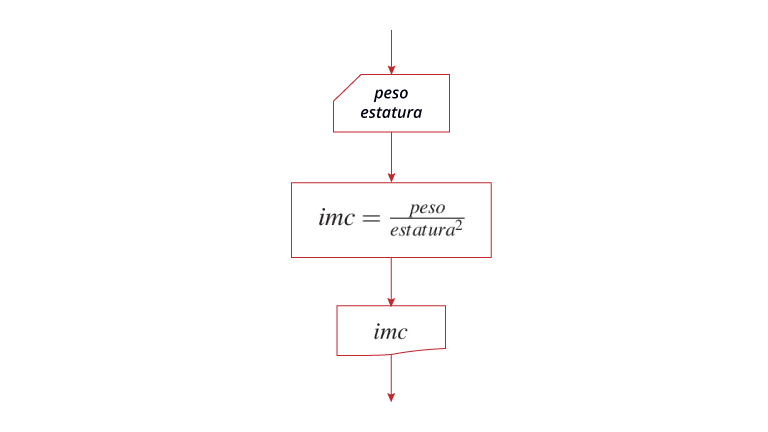
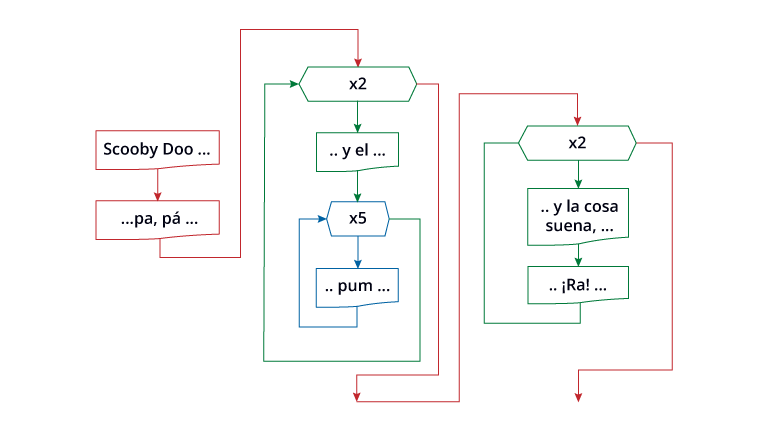
Para poder identificar un problema secuencial es necesario comprender que estos se clasifican con base en la estructura que se necesita en el diseño de la solución (algoritmo) que vamos a seguir. Los problemas secuenciales entonces, se resuelven utilizando secuencias de instrucciones, los cuales tienen la característica de que los pasos se aplican uno después de otro, en un orden consecutivo. Cada paso se ejecuta de tal modo que la salida de dicha tarea es la entrada del siguiente paso y así sucesivamente hasta terminar el trabajo.
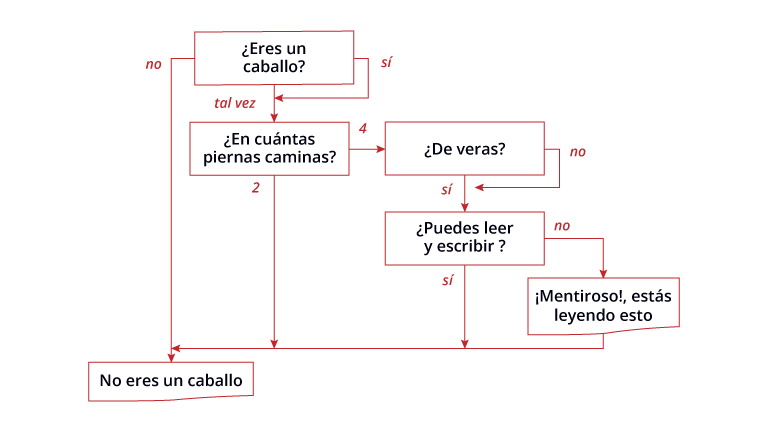
Los problemas condicionales tienen la característica de que el flujo de la solución del problema va a depender del valor de verdad de una condición. Utilizando el valor de una o varias entradas, se puede tomar un camino u otro para resolver el problema. Por tanto, estos problemas necesitan de un algoritmo condicional que utiliza proposiciones lógicas para ser resuelto. La estructura del algoritmo condicional utiliza una comparación de valores para obtener un resultado, que de ser verdadero nos llevará a la ejecución de ciertas acciones o de ser falso, nos permitirá ejecutar otras, es decir, el resultado indicará la ruta o camino que seguirá el algoritmo. Esta decisión está basada en que un valor de entrada cumpla o no con una condición y dependiendo de si se concreta o no esta condición, se realizará una acción u otra.
Un caso particular de los problemas condicionales corresponde a los ciclos o estructuras que se repiten mientras la condición sea verdadera o exista un evento que interrumpa la acción.
Escribe el tipo de problema al que refieren los ejemplos de la siguiente tabla: determinístico, probabilístico, secuencial, condicional o cíclico. Pueden aplicar varias categorías a cada problema como en el ejemplo.