Jesús Salinas
Alexander Maz
Introducción
En este trabajo, realizamos un estudio exploratorio considerando la dimensión histórica de las matemáticas, para lo cual, se elaboró un experimento de enseñanza (Steffe & Thompson, 2000). El enfoque histórico se tomó con una doble función: para mostrar un rostro humano de las matemáticas, considerando su papel en la cultura (Fauvel, 1991; Bishop, 1995) y, con base en esto, observar el uso que hacen estudiantes del nivel bachillerato de instrumentos psicológicos de la aritmética pitagórica (Vygotsky, 1995; Kozulin, 2000; Wertsch, 1988). Nos interesa explorar si este enfoque, considerando la aritmética, puede contribuir para introducir a los alumnos a la demostración.
Consideramos el tema de los números poligonales, el cual fue abordado por los pitagóricos como parte de una temprana teoría de números, que ha seguido teniendo frutos a lo largo de la historia (Weil, 1984; Dickson, 1971; Duke, 1997; Guy, 1994). Existen múltiples trabajos que han abordado el tema de los números poligonales, tanto para reflexionar desde un punto de vista cognitivo como para realizar propuestas de tipo curricular (Andrew, 1990; Norman, 1991). Hay también estudios sistemáticos con aparatos conceptuales y metodológicos distintos (Clarkson, 1962; Weaver, 1974; Castro, 1995). Un antecedente más directo con este trabajo, es un estudio exploratorio, en el cual se utiliza el tema de los números poligonales con el propósito de iniciar a los 314 alumnos, en la elaboración de un razonamiento deductivo, para justificar un resultado geométrico (Salinas, 2010).
Problema de investigación
¿Cuál es la manera en que alumnos de primer semestre de bachillerato realizan actividades que involucran el reconocimiento de patrones aritméticos y geométricos, a partir de utilizar diagramas de la aritmética pitagórica? Y, en este contexto, ¿qué aptitudes manifiestan para realizar una demostración?
Marco teórico
Nuestra perspectiva central es que la interacción entre la historia de las matemáticas y la educación matemática ayuda a construir estrategias que contribuyen al proceso de enseñanza de las matemáticas (Fauvel & Maanen, 2000; Maz, 1999).
Consideramos diferentes ideas que se enmarcan en la perspectiva sociocultural de Vygotsky (1995). En ésta, el proceso de aprendizaje es considerado un proceso de apropiación de los métodos de acción y de representación de una cultura dada (Radford, 1997). En dicha apropiación, los instrumentos psicológicos o simbólicos desempeñan una función esencial en el desarrollo cognitivo (Wertsch, 1988). El enfoque vygoskiano considera tres tipos de mediadores. La interacción social, el uso de herramientas y los instrumentos psicológicos. En este estudio centramos la atención fundamentalmente en la utilización de instrumentos psicológicos1. Los instrumentos psicológicos son los recursos simbólicos – signos, símbolos, textos, formulas, medios gráfico-simbólicos – que ayudan al individuo a dominar sus propias funciones psicológicas “naturales” de percepción, memoria, atención, etc. (Kozulin, 2000, p. 15)2. Una afirmación central de este enfoque teórico, es que “el carácter simbólico de los instrumentos psicológicos permite la adquisición de aptitudes generalizadas. Así, en lugar de aprender una tarea o una operación particular, el niño adquiere un principio más general que es aplicable a distintas tareas. Este enfoque generalizado se hace posible mediante el desarrollo de modelos simbólicos de representación para todo el grupo de tareas.” (Ibid. P. 64). Por aptitudes generalizadas entendemos aquí, aquellas que requieren los alumnos para tratar con la tarea de demostrar un enunciado general.
Metodología
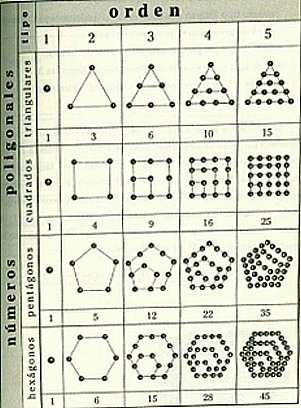
De acuerdo con nuestro marco teórico, en las actividades que se llevaron a cabo estuvieron implicados grupos de personas con una interacción social determinada y la práctica comunicativa. Las actividades que se diseñaron se resolvieron en parejas. Las intervenciones del profesor-investigador estuvieron orientadas a describir previamente el contexto histórico en el que se desarrolló la aritmética pitagórica y en explicar las ideas filosóficas centrales de los pitagóricos acerca de los números. Posteriormente, en las siguientes sesiones, los estudiantes debían observar e interpretar los patrones aritméticos y geométricos que se representan en la fig. 1, y resolver los problemas que adaptamos de la aritmética pitagórica.
Figura 1. Representación de los números triangulares, cuadrados, pentagonales y hexagonales. Tomado, de González Urbaneja (2009).
La población de estudio
La población observada fue un grupo de 24 alumnos de primer semestre del bachillerato del Colegio de Ciencias y Humanidades, UNAM, durante las actividades escolares de un curso ordinario. Participaron 12 hombres y 12 mujeres con edades entre 15 y 16 años.
Procedimiento
Se llevó a cabo una secuencia didáctica en la que se realizaron diversas actividades. La duración fue de 6 horas. En dos sesiones de una hora, cada una, el profesor-investigador describió y explicó a los estudiantes algunas ideas centrales del pensamiento numérico de los pitagóricos, en el marco de su contexto cultural. En las siguientes tres sesiones, dos con una duración de hora y media y una de una hora, los estudiantes, debían observar e interpretar los patrones aritméticos y geométricos que se representan en la fig. 1, y resolver algunos problemas que adaptamos de la aritmética pitagórica. Las actividades las realizaron en parejas constituidas por los propios estudiantes.
Análisis de los contenidos matemáticos implicados en las actividades
Los números poligonales fueron utilizados por grandes matemáticos, que han destacado en la teoría de los números, como Fermat, Pascal, Gauss, Dirichlet, Lagrange, Legendre, entre otros (Guy, 1994; Duke, 1997).
Asimismo, siguen dando frutos en el desarrollo de investigaciones de actualidad en la teoría de números (Duke, 1997). Estos números se forman por puntos que describen polígonos regulares (Fig. 2). Las figuras geométricas que construyeron los pitagóricos con los números poligonales, proporcionan una evidencia visual de numerosas propiedades de los números naturales. De esta manera, estos diagramas han mostrado ser heurísticamente ricos, por ejemplo, para establecer relaciones entre propiedades de órdenes consecutivos de números de un 316 determinado tipo, así como relaciones entre números poligonales de tipos diferentes. Todas estas propiedades y relaciones se obtienen de simples comprobaciones aritméticas. Sin embargo, su prueba requiere de un simbolismo algebraico.
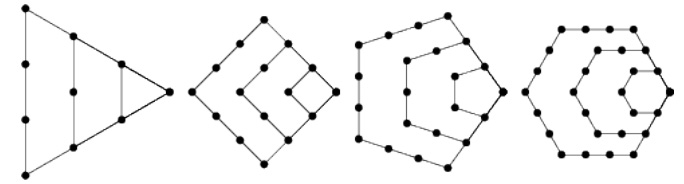
Figura 2. Esta figura ha sido tomada de Weisstein (2011).
Los diagramas anteriores, Fig. 2, ilustran gráficamente el proceso mediante el cual los números poligonales se construyen. La regla para formar un número triangular es agregar, a cada triangulo de lado n, un lado con n+1 puntos, así obtenemos 1, 3, 6, 10, 15, 21, ... que resultan de la serie 1+2+3+4+5+6... Por lo tanto, el n-ésimo número triangular está dado por T(n) = [n · (n+1)]/ 2.
La misma observación de las figuras señala que T(n) = T(n-1)+n, donde T(1) = 1, lo cual proporciona una definición recursiva de números triangulares que permite obtener cada uno de ellos en términos del número anterior. Similarmente, los diagramas ilustran como construir los demás números poligonales a partir de los números triangulares. Por ejemplo, es posible observar que todo número cuadrado es la suma de dos números triangulares sucesivos.
1+3=4
3+6=9
6+10=16,
Es decir, C(n)= T(n)+T(n-1) (Teorema de Teón de Esmirna (González Urbaneja, 2009))
C(n)= [n·(n+1)]/2 + [(n-1)·n]/2 = n2
Además, podemos observar cual es la regla recursiva para la construcción de los números cuadrados C(n) = n2.
1+3=22
1+3+5=32
1+3+5+7=42
1+3+5+7+9=52,
En general, C(n)= C(n-1)+(2n-1), C(1)=1.
Esto además pone de manifiesto la relación entre los números cuadrados con los números impares.
Instrumentos de observación
Para la toma de datos se diseñó una serie de actividades relacionadas con la aritmética pitagórica. Los datos que se obtuvieron fueron tomados de las hojas de actividades realizadas en el salón de clase. Tales datos fueron expresados en forma de textos y se realizó un análisis cualitativo de ellos. En la primera sesión nos interesó observar si los alumnos interpretan adecuadamente los patrones aritméticos y geométricos del diagrama de la Fig. 1. En la segunda sesión, quisimos observar si los estudiantes establecen conexiones entre la secuencia numérica, la secuencia de representaciones geométrica y la secuencia de desarrollos aritméticos, de los números poligonales. Y, si aplican estas conexiones para caracterizar otros números poligonales. Finalmente, de acuerdo con alguna de las técnicas que utilizaba Vygotsky en sus experimentos que “consistía en imponer al pequeño una tarea que superara su conocimiento y 317 capacidades, a fin de descubrir los comienzos rudimentarios de nuevas habilidades” (Vygotsky, 2009, p. 34); nos propusimos observar que hacen estos estudiantes al pedirles probar un teorema de la aritmética pitagórica.
Resultados y discusión
Primera sesión
Actividad: Indica los números triangular, cuadrado, pentagonal y hexagonal que siguen a los que están en la tabla; y dibújalos.
| Parejas alumnos | Dibujan los números poligonales | Identifican el siguiente número | Proponen fórmulas para el término n-ésimo |
|---|---|---|---|
| 10, 14 | Si | Si | Si |
| 11 | Si | Si | Si |
| 2, 19 | * | Si | No |
| 1, 20 | * | Si | No |
| 8, 24 | Si | Si | No |
| 15, 21 | Si | Si | No |
| 12, 16 | Si | Si | Si |
| 13 | Si | Si | Si |
| 17, 18 | Si | Si | No |
| 5, 23 | Si | Si | Si |
| 11, 26 | * | Si | No |
| Total | 11 | 11 | 5 |
Tabla 1. Resultados de la actividad de la primera sesión
El 100% de alumnos indican lo que se pide, aunque sus respuestas tienen diversas características. Algunos alumnos, 25%, no dibujan bien el número pentagonal y hexagonal (*). 33.3% de estudiantes escribe la sucesión completa de números, incluso con más términos que el que se solicita. La mitad de estos últimos dibujan la sucesión de polígonos regulares y las sucesiones de números, para mostrar la correspondencia entre estas dos formas de registro de representación. Así, se observa que todos ellos reconocen, con diversos matices, los patrones geométricos y los patrones aritméticos que se encuentran en la fig. 1. Vinculan ambos tipos de patrones de representación y dan continuidad a las secuencias de números representados. No obstante que no se pide, 41.6%, casi la mitad de las parejas, proponen expresiones algebraicas para el término n-ésimo.
Segunda sesión
- Indica las series a partir de las cuales se forman los números poligonales que aparecen.
- Escribe los números poligonales que siguen, hasta los números decagonales. Asimismo, escribe las series que permiten formar dichos números.
- Dibuja el patrón geométrico que permite construir las figuras de la tabla.
| Parejas alumnos | Identifican las series de la tabla | Escriben los siguientes números | Dibujan patrón geométrico |
|---|---|---|---|
| 2, 19 | Si | Si | No |
| 11 | Si | * | No |
| 4, 6 | Si | * | No |
| 7, 17 | Si | Si | Si |
| 8, 24 | Si | * | Si |
| 15, 21 | Si | Si | No |
| 9, 25 | Si | Si | Si |
| 1, 20 | Si | * | * |
| 12, 16 | Si | Si | Si |
| 13, 20 | Si | No | * |
| 5, 23 | Si | 1/0 | * |
| 10, 14 | Si | Si | Si |
| Totales | 12 | 11 | 8 |
Tabla 2. Resultados de las actividades de la segunda sesión
Prácticamente el 100% de estudiantes responden correctamente las dos primeras preguntas. 33.3% de ellos, escriben los números poligonales hasta el decagonal, pero solo escriben las sucesiones y no las series (*). Las sucesiones las hallan observando verticalmente la tabla. Una pareja presenta errores en algunas de las series (1/0). En general, los resultados reflejan que los alumnos realizan un cierto análisis estructural de números que comparten un mismo patrón de representación, y obtienen el desarrollo aritmético que comparten los términos de una misma secuencia. Así, establecen conexiones entre la secuencia numérica, la secuencia de representaciones geométrica y la secuencia de desarrollos aritméticos. Estos resultados son congruentes con los obtenidos en otros estudios (Castro, Rico y Romero, 1997).
Asimismo, aplican estas conexiones para caracterizar otros números poligonales. Esto refleja una cierta interiorización del diagrama de la fig. 1, que está operando como un instrumento psicológico en la realización de las actividades. Finalmente, con relación a dibujar el patrón geométrico que permite dibujar a los números poligonales de un mismo tipo, 66.6% de los estudiantes responde correctamente.
Tercera sesión
Actividad: Demostrar que todo número cuadrado es la suma de dos números triangulares sucesivos.
| Parejas alumnos | Representación Aritmética | Representación Geométrica | Manipulación Geométrica | Indicios de prueba |
|---|---|---|---|---|
| 2, 19 | Si | Si | No | No |
| 11 | No | No | No | No |
| 4, 6 | Si | Si | No | No |
| 7, 17 | Si | Si | No | Si |
| 8, 24 | Si | Si | No | No |
| 15, 21 | Si | Si | No | Si |
| 9, 25 | Si | Si | No | No |
| 1, 20 | Si | Si | No | No |
| 12, 16 | Si | Si | Si | No |
| 13, 20 | Si | Si | No | No |
| 5, 23 | Si | Si | No | No |
| 10, 14 | Si | Si | Si | Si |
| Total | 12 | 11 | 2 | 3 |
Tabla 3. Resultados de la actividad de la tercera sesión
Los alumnos manifiestan, como se muestra en la tabla anterior, habilidad para la representación aritmética y geométrica de los números poligonales (en este caso triangulares y cuadrados). Sin embargo, para probar el enunciado general, ocho parejas (66.6% de alumnos) solo responden poniendo ejemplos. Dibujan casos de dos números triangulares sucesivos y el número cuadrado resultante. Tres parejas (25% de los alumnos) presentan indicios de percibir el carácter general de la tarea. Sin embargo, ningún alumno intenta una prueba general. El tipo de errores que cometen son los siguientes: Sólo un alumno muestra dificultad para interpreta el enunciado. Lo más recurrente (8 parejas) es mezclar los registros de representación, es decir, ponen el signo “+” entre dos triángulos y como resultado de esa “operación” un cuadrado. Incluso, una pareja agrega otro código con colores, para acentuar la evidencia visual. Es claro que estos argumentos aún no pueden ser calificados totalmente como una demostración en el sentido matemático más estricto, pero son pruebas que pretenden validar el enunciado (Balacheff, 1987).
A continuación se muestran diferentes tipos de prueba que elaboran los estudiantes.
En la génesis de la demostración Balacheff (1987) distingue principalmente las pruebas pragmáticas y las intelectuales. El tipo más sencillo de prueba pragmática es el empirismo ingenuo, que consiste en asegurar la validez de un enunciado después de haberlo verificado en algunos casos. La respuesta de la fig. 3 es de este tipo, pero, también se observa el intento de dar una prueba que no se basa en un representante particular. Los alumnos parecen estar en una fase de transición para superar una prueba pragmática.
Prácticamente en todos los estudiantes subyace una idea inductiva, característica de las ciencias experimentales, que para el caso de las matemáticas confunde dos procesos distintos: la construcción del conocimiento y la prueba de su verdad.
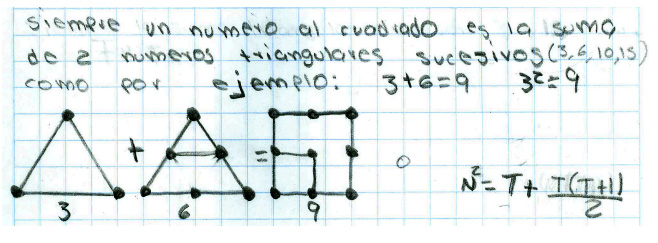
Figura 3. Este tipo de prueba es una prueba pragmática.
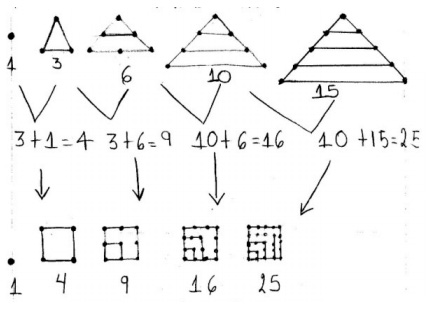
Fig. 4. En esta respuesta los alumnos pretenden dar una prueba inductiva del enunciado.
Tres parejas (25%) dan respuestas en las cuales realizan una reconfiguración geométrica para mostrar que se cumple el enunciado.
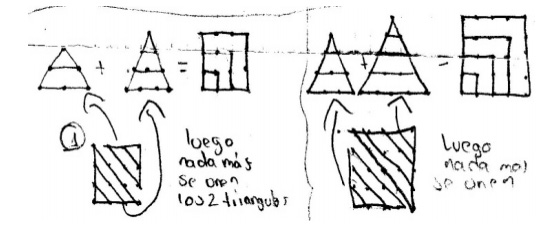
Figura 5. Este tipo de respuesta muestra habilidad de alumnas para hacer un tratamiento
figural para acomodar las distintas formas geométricas y relacionarlas.
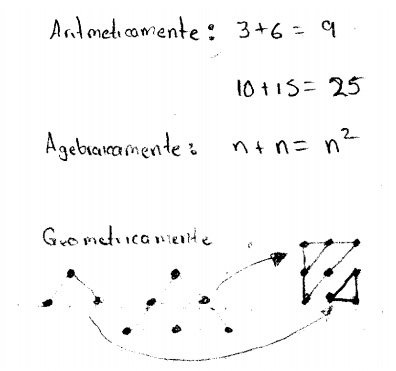
Figura 6. En esta respuesta se usan distintos registros de representación que intentan probar la verdad del teorema en cuestión. Sin embargo, utiliza de manera errónea el álgebra
Conclusiones
Nuestro problema de investigación está conformado por dos preguntas. ¿Cuál es la manera en que alumnos de primer semestre de bachillerato realizan actividades que involucran el reconocimiento de patrones aritméticos y geométricos, a partir de utilizar diagramas de la aritmética pitagórica? Y, en este contexto, ¿qué aptitudes manifiestan para realizar una demostración? Con relación a la primera podemos responder lo siguiente:
Se observa que todos los alumnos reconocen, los patrones geométricos y aritméticos que se encuentra en la fig. 1, la conversión (Duval, 1999), es decir, el pasaje de un registro de representación a otro se da de manera espontánea. Los alumnos vinculan ambos patrones de representación y dan continuidad a las secuencias de números representados. Esta situación les permite realizar tareas donde trabajan con sucesiones y series de números y relaciones entre ellas, es decir hay un desarrollo en el tratamiento del registro de representación aritmético (Duval, 1999). Además, un número considerable de estudiantes manifiestan espontáneamente interés en utilizar expresiones generales para caracterizar los diferentes tipos de números poligonales. Asimismo, algunos alumnos desarrollan un cierto tratamiento del registro de representación geométrico.
Por consiguiente, podemos afirmar que sin instrucción explicita los alumnos desarrollan un proceso de interiorización de los diagramas pitagóricos de los números poligonales. Esta situación da pauta a afirmar, que este experimento de enseñanza, basado en un trabajo colaborativo de interacción interpersonal, contribuye a la construcción de conceptos aritméticos y su representación geométrica, asimismo, ayuda a que los alumnos desarrollen diferente tipo de argumentos, apoyados en propiedades de los números, para validar una proposición matemática.
Con relación a la segunda pregunta podemos observar que este estudio exploratorio nos proporciona pistas sobre algunos comienzos rudimentarios de algunas, posiblemente nuevas, aptitudes para demostrar; que manifiestan algunos alumnos: 1. El reconocimiento del carácter general de un enunciado matemático; 2. La elaboración de argumentos para probar un enunciado, incluso la intensión de probar usando el simbolismo algebraico y 3. Dan un tratamiento geométrico de los números triangulares 322 para mostrar su relación con los números cuadrados y así intentar probar la relación entre distintos tipos de números.
Por otra parte, el estudio proporciona información de diferentes errores y del tipo de desarrollo cognitivo que los alumnos podrían seguir para probar un enunciado general de la aritmética, lo cual proporciona elementos para seguir profundizando en el problema de investigación planteado.
Reconocimiento
Este trabajo ha sido realizado en el marco de la estancia sabática en el Departamento de Matemáticas de la Facultad de Ciencias de la Educación, UCO. Beca otorgada por la Dirección General de Asuntos del Personal Académico de la Universidad Nacional Autónoma de México, enero-diciembre de 2011.
Salinas, J. y Maz, A. (2011). La aritmética pitagórica como un recurso para la introducción a la demostración. En J. L. Lupiáñez, M. C. Cañadas, M. Molina, M. Palarea, y A. Maz (Eds.), Investigaciones en Pensamiento Numérico y Algebraico e Historia de la Matemática y Educación Matemática - 2011 (pp. 313-323). Granada: Dpto. Didáctica de la Matemática, Universidad de Granada.
1Según Vygotsky, existen tres clases principales de agentes mediadores: instrumentos materiales, instrumentos psicológicos y mediadores humanos. (…) Pero los instrumentos psicológicos simbólicos desempeñan un papel aún más importante porque ocupan una posición estratégica “entre” los estímulos del mundo y los procesos psicológicos internos de un individuo. Por lo tanto, los instrumentos psicológicos transforman la interacción no mediada del ser humano con el mundo en una interacción mediada” (Kozulin, 2000, pp. 17-18).
2Aquí, proponemos relacionar la noción de instrumento psicológico de Lev Vygotsky con la noción de registros de representación semiótica, de Raymond Duval, es decir, el lenguaje natural, los lenguajes simbólicos, los gráficos, las figuras geométricas, diagramas, esquemas, etc.(Duval, 1999).
Referencias
Andrew, P. (1990). Generalising number patterns. Mathematics in School, 9-13.
Balacheff, N. (1987). Processus de prueve et situations de validation; Educational Studies in Mathematics 18, 147-176.
Bishop, A. J. (1995). Mathematics education between technology and ethnomathematics: should it be common? Does it make sense? Proccedings of CIEAEM 45, 53-62.
Castro Martínez, E. (1995). Exploración de patrones numéricos mediante configuraciones puntuales. Granada: Edit. Comares.
Castro Martínez, E., Rico Romero, L. & Romero Albaradejo, I. (1997). Sistemas de representación y aprendizaje de estructuras numéricas; Enseñanza de las Ciencias, 15(3), 361-371.
Clarkson, D. (1962). Taxicab Geometry, rabbits, and Pascal`triangle-discoveries in a sixth-grade classroom. Arithmetics Teacher, 308-313.
Dickson, L. E. (1971). History of the theory of numbers, II, Chelsea Publishing.
Duval, R. (1999). Semiosis y pensamiento humano. Registros semióticos y aprendizajes intelectuales. Cali, Colombia: Universidad del Valle.
Duke, W. (1997). Some old problems and new results about quadratic forms. Notices of the AMS 44(2), 190-196.
Fauvel, J. (1991). Using history in mathematics education. For learning of mathematics. 11 (2), 13-16.
Fauvel, J. & Maanen, J. V. (2000). History in Mathematics Education: the ICMI study, Dordreght: Kluwer Academic Publisher.
González Urbaneja, P. M., (2009). Pitágoras. El filósofo del número. Madrid: Nivola libros y ediciones.
Guy, R. K. (1994). Every number is expressible as a sum of how many polygonal numbers? Amer. Math. Monthly 101, 169-172.
Kozulin, A. (2000). Instrumentos Psicológicos. Barcelona: Paidós.
Maz, A. (1999). Historia de la matemática en clase: ¿por qué y para qué? En Berenger, Mª. I.; Cardeñoso, J. Mª. y Toquero M. (Eds.)(1999). Investigación en el aula de 323 matemáticas. Matemáticas en la sociedad. Granada: Sociedad Thales y Departamento de Didáctica de la matemática.
Norman, F. A. (1991). Figurate Numbers in the classroom. Arithmetic Teacher, 42-45.
Radford, L. (1997). L`invention d`une idée mathematique: la deuxieme inconnue en algebra. Repères, Revue des IREMs 28 (july), 81-96
Salinas, J. (2010). El uso de la historia de las matemáticas para el aprendizaje de la geometría en alumnos del bachillerato. En M. M. Moreno, A. Estrada, J. Carrillo, & T. A. Sierra (Eds.), Investigación en Educación Matemática XIV Lleida: SEIEM. pp. 557-568.
Steffe, L. y Thompson, P. W. (2000). Teaching experiment methodology: underlying principles and essential elements. En A. E. Nelly y R. A. Lesh (Eds). Handbook of research design in mathematics and science education (pp. 267-306). Mahwah: NJ: Lawrence Erlbaum.
Vygotsky, L. S. (1995). Pensamiento y Lenguaje. Barcelona: Paidós.
Vygotsky, L. S. (2009). El desarrollo de los procesos psicológicos superiores. Barcelona: Crítica.
Weaver, C. (1974). Figurate Numbers. Mathematics Teacher, 661-666.
Weil, A. (1984). Number theory. An approach through history. Birkhäuser.
Weisstein, E. W. (2011). Polygonal Number, Mathword-A Wolfram Web Resource. http://mathworld.wolfram.com/PolygonalNumber.html
Wertsch, J. (1988). Vygotsky y la formación social de la mente. Barcelona: Paidos.
