En los ejemplos anteriores hemos visto el esqueleto de las clases, y pudo observarse que el operador de asignación en pseudocódigo es el símbolo de igual, y de hecho se considera un operador, por lo que a = b = c; se resuelve de derecha a izquierda (sería equivalente a b c y después a b, por lo que a y b tomarían el valor de c).
La asignación () se representa con un igual “=”, mientras que cuando se quieren comparar dos cantidades se utiliza el igual doble “==”. La expresión a=b es equivalente a a b, el valor de b se lo asigna a a; mientras que a==b es una pregunta para saber si a es igual a b.
Las expresiones que regresan valores en un lenguaje de programación tienen que serializarse en una sola línea, a diferencia de cómo se manejan en el dominio del problema. Java, al igual que otros lenguajes de programación no manejan potencias ni raíces.
Se explicarán cuatro grupos de operadores:
- numéricos (aplica a enteros y de punto decimal)
- lógicos (booleanos) y de comparación
- alfanuméricos (texto)
- operador ternario
- uso de funciones
Para encontrar las variables que se requieren, hay que observar las operaciones de asignación y de lectura de datos en los diagramas de flujo o pseudocódigos disponibles.
A continuación, se muestran los operadores ordenados de mayor a menor jerarquía o prioridad de operación, por cada grupo de información de sus operandos:
Se utilizan para realizar operaciones con enteros o de punto flotante.
Operadores básicos
|
Unarios |
- |
negativo |
|
++ |
incremento prefijo (sólo enteros) |
|
|
-- |
decremento prefijo (sólo enteros) |
|
Paréntesis |
( ) |
permite agrupar |
|
Llamada a método que regresa un valor (función) |
|
Multiplicación y división |
* |
multiplicación |
|
/ |
división |
|
|
% |
módulo o residuo |
|
Suma y resta |
+ |
suma |
|
- |
resta |
|
Incremento / decremento posfijo |
++ |
incremento posfijo |
|
-- |
decremento posfijo |
|
Operadores de bits sólo enteros) |
& |
and |
|
| |
or |
|
|
^ |
xor |
|
|
~ |
not |
|
|
>> |
Corrimiento a la derecha |
|
|
<< |
Corrimiento a la izquierda |
|
Asignación |
+= -=, *= /=, %= &= |= ^= |
Acumuladores realiza la operación indicada sobre sí mismo |
|
= |
Asignación () |
Operadores básicos
Los paréntesis, el símbolo de negativo, la suma, la resta y la división son iguales a la forma tradicional. Para la multiplicación se ocupa un asterisco, para la división una diagonal y el símbolo de porcentaje para obtener el residuo de la división.
No olvides poner paréntesis cuando se requiera agrupar expresiones. Probablemente no sea necesario en la siguiente expresión para calcular el área de un triángulo.
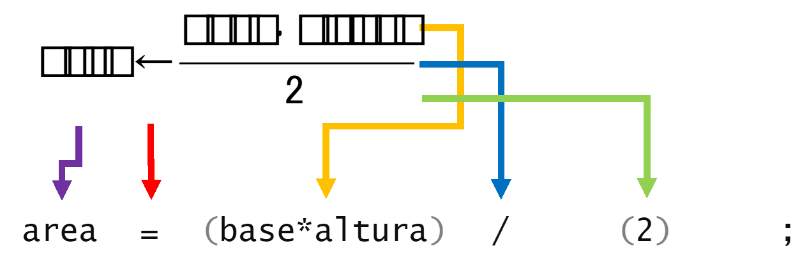
Pero en esta operación si se requerirán:
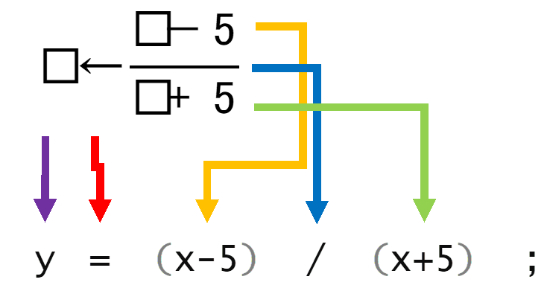
En las divisiones
{
X = 23 / 16; // regresa el resultado de la división (1)
X = 23 % 16; // regresa el residuo de la división (7)
}
Operadores de bits
Estas operaciones aplican para cada bit, por lo que para entender su comportamiento hay que operar en base 2 de una variable entera, utilizando las operaciones booleanas AND (representada por el ampersand “&”), OR (representada por la barra vertical “|”), NOT (es un operador unario y utiliza la tilde “~”, es el equivalente al operador “complemento a “2”), y XOR (se utiliza el acento circunflejo ”^”), se opera 1 a 1 y sin acarreos:
Ejemplo con XOR:

Los corrimientos a la izquierda y a la derecha equivalen a multiplicar o dividir entre 2n o mover la cantidad en binario n posiciones a la izquierda o derecha, pero lo que salga del tamaño de la variable se elimina, y los espacios vacíos se rellenan con ceros. Estos operadores se utilizan en las multiplicaciones.
| Operador | Operación | Aplicación matemática |
|---|---|---|
| x = y <<< /span>n; | Acarreo a la izquierda, n bits | Multiplicar por 2n |
| x = y>>n; | Acarreo a la derecha, n bits | Dividir entre 2n |
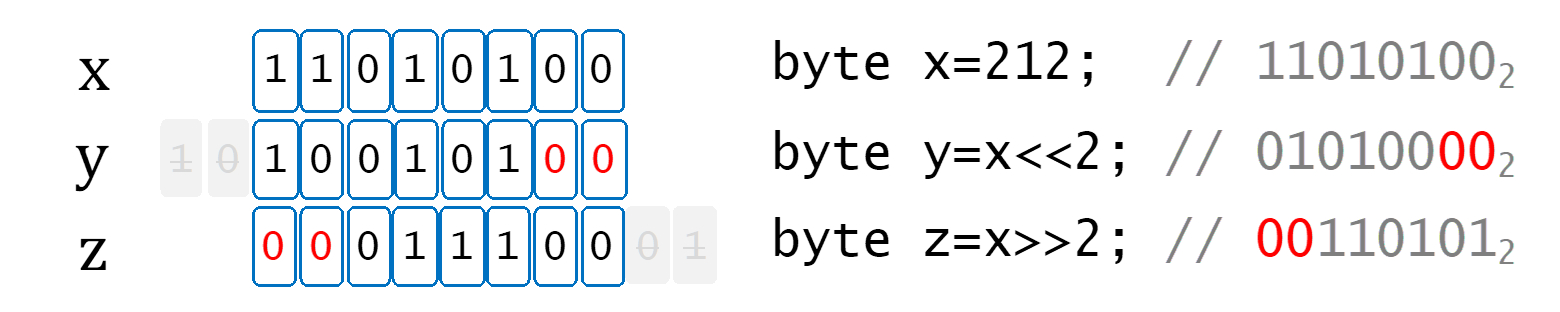
Operadores de incremento
Cuando se realizan asignaciones, se opera la expresión del lado izquierdo de la igualdad, una vez que se calcula el resultado, se asigna a la variable del lado izquierdo. Expresiones de la forma x←x+algo; se conocen como acumuladores y pueden quedar:
| Versión completa | Versión de acumulador | Operación | Aplicación matemática |
|---|---|---|---|
| x = x+algo; | x += algo; | Acumular suma | $x = \sum algo$ |
| x = x–algo; | x -= algo; | Acumular resta | $x = \sum algo$ |
| x = x*algo; | x *= algo; | Acumular multiplicación | $x = \prod algo$ |
| x = x/algo; | x /= algo; | Acumular división | |
| x = x&algo; | x &= algo; | Acumular AND por bits | |
| x = x|algo; | x |= algo; | Acumular OR por bits | |
| x = x^algo; | x ^= algo; | Acumular XOR por bits |
Cuando “algo” = 1, pueden aplicarse las siguientes operaciones:
| Versión completa | Versión de acumulador | Incremento prefijo | Incremento posfijo | Operación |
|---|---|---|---|---|
| x = x+1; | x += 1; | ++x; | x++; | incremento |
| x = x–1; | x -= 1; | --x; | x--; | decremento |
El operador de incremento o decremento es unario y puede ir dentro de una expresión, pero el que el operador sea prefijo trabaja de manera distinta. Cuando es prefijo se actualiza el valor de la variable antes de operarse la expresión, si es postfijo lo opera después:
Por ejemplo:
| Operación | Expresión | Equivale a |
|---|---|---|
| Prefijo | x = ++a + b ; | a = a+1; x = a+b; |
| Posfijo | x = a++ + b ; | x = a+b; a = a+1; |
Regresan valores: verdadero (true) o falso (false):
| Negación | ! | not |
|---|---|---|
| Paréntesis | ( ) | permite agrupar |
| Operadores lógicos | && | and lógico o booleano |
| || | or lógico o booleano | |
| ^ | xor lógico o booleano | |
| Relacionales | == | igual |
| != | distinto | |
| << /span> | Menor que | |
| <=< /span> | Menor o igual que | |
| > | Mayor que | |
| >= | Mayor o igual que |
| Juntar dos cadenas | + | Concatenación |
|---|---|---|
| Acumular dos cadenas | += | Concatenación con acumulación |
Ejemplo:
String nombre, apellidos, nombreCompleto;
nombre = "Juan";
apellidos = "Pérez Pérez";
// concatenación:
nombreCompleto = nombre + " " + apellidos; // asignará: “Juan Pérez Pérez”
// Es equivalente a la concatenación con acumulación;
nombreCompleto = nombre; // valor inicial: nombre
nombreCompleto += " "; // agregar un espacio
nombreCompleto += apellidos; // agregar los apellidos

El operador ternario evalúa una expresión booleana (falso o verdadero), y va seguido del símbolo de interrogación “?”, después el valor que tendría si la expresión booleana es verdadera seguido de dos puntos “:”, seguido del valor si la expresión fuera falsa. Los valores que aparecen después de ambos símbolos deben ser del mismo tipo.
String mensaje;
mensaje = (edad>=18) ? "Tramita tu credencial de elector" : "Hola";
// expresión valor si es verdadero valor si
// booleana es falso
Pueden utilizarse métodos que regresan valor, pueden se métodos de clase (no se requiere instanciar la clase) o métodos de instancia (se necesita instanciar o crear un objeto) de la clase para poder utilizarlo. Como se mencionó, en Java no existe el operador de potencia o raíz, pero la clase Math contiene varias funciones que se utilizan mucho:
| $\sqrt(x)$ | Math.sqrt(x) | raíz cuadrada |
| $x^p$ | Math.pow(x,p) | elevar x a la potencia p |
| $x^p$ | Math.pow(x,p) | elevar x a la potencia p |
| $\sqrt[r]{x}$ | Math.pow(x,1/r) | sacar raíz de orden r |
| $e^x$ | Math.exp(x) | Elevar e a la potencia x |
| $n(x)$ | Math.ln(x) | Logaritmo natural de x |
| $|x|$ | Math.abs(x) | Valor absoluto de x |
| $sen(x)$ | Math.sin(x) | Seno de x (en radianes) |
| $cos(x)$ | Math.cos(x) | Coseno de x (en radianes) |
| $tan(x)$ | Math.tan(x) | Tangente de x (en radianes) |
| $tan^{-1}(x)$ | Math.atan(x) | Arco cuya tangente es x (en radianes) |
| $\pi$ | Math.PI | Constante $\pi$ |
| Otras | Documentación de la clase Math |
Ejemplos
Codifique en Java las siguientes expresiones:
Área de un rectángulo: $area \leftarrow base \times altura$
double área;
//…
area = base * altura;
Índice de masa corporal de una persona:$imc \leftarrow \tfrac{peso}{ estatura^2 }$
double imc, peso, estatura;
//…
imc = peso / Math.pow( estatura, 2 );
Ahora codifique en Java los siguientes pseudocódigos:
| Pseudocódigo | Codificación en java |
| $y \leftarrow 45 + 25 \times 10$ | y=45+25*25; |
| $z \leftarrow \tfrac{1}{3}$ | z=1/3; |
| $a \leftarrow \tfrac{1}{3+a}$ | a=1/(3+a); |
| $V \leftarrow R I$ | V=R*I; |
Escribe la respuesta correcta en los espacios correspondientes para completar la codificación:
Ejercicio 1
Área de un círculo $area \leftarrow \pi \times radio^2$
Ejercicio 2
Cálculo de las raíces de una ecuación de segundo grado: $x=\tfrac{ -b \pm \sqrt{b^2-4ac} }{ 2a }$


