Para los siguientes ejemplos vamos a revisar una secuencia de aprendizajes con el fin de mostrar en cada uno de ellos cómo se van integrando las herramientas vistas en este objeto de aprendizaje, hasta lograr el circuito lógico simulado.
La secuencia que vamos a revisar es la siguiente:
- Planteamiento del problema
- Tabla de verdad
- Obtención de las funciones booleanas
- Diagrama del diseño lógico
- Construcción o simulación del circuito lógico
Implementación de una compuerta AND de tres entradas con compuertas de dos entradas
I. Planteamiento del problema
La implementación de una compuerta AND de tres entradas basándose en compuertas AND de dos entradas, es muy sencillo ya que una compuerta AND de múltiples entradas puede ser conectada a compuertas simples en serie, una atrás de la otra. El único problema de implementar compuertas en cascada, es que el tiempo de la señal aumenta desde la entrada hasta la salida. Si necesitamos una compuerta AND de 3 entradas y no una hay alguna en ese momento disponible, es fácil ya que su implementación se basa en un solo circuito integrado, el 7408 es un encapsulado que contiene 4 compuertas AND de dos entradas cada una.

II. Tabla de verdad
La tabla de verdad de una función AND de dos entradas es la siguiente:
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Para la función AND de tres entradas, la tabla de verdad quedaría:
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
III. Obtención de la función booleana
| La expresión booleana que representa la función AND de tres entradas es: | $S=A \cdot B \cdot C$ |
| Por lo que la simplificación de la función booleana para la implementación de una compuerta AND de tres entradas utilizando un circuito integrado 7408 (AND de 2 entradas): | $S=(A \cdot B) \cdot C$ |
IV. Diagrama del diseño lógico
El símbolo para la compuerta AND de dos entradas:
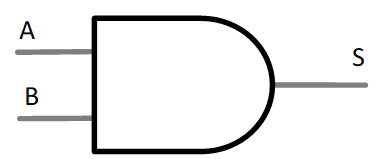
El diagrama lógico para esta implementación se muestra en la siguiente figura. Se realizó de acuerdo a la función que tenemos para la salida (S), con sus entradas A, B y C.
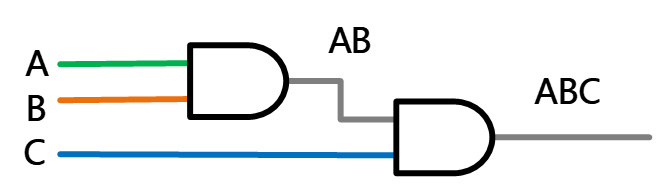
V. Construcción o simulación del circuito lógico
Para hacer el arreglo vamos a utilizar el software Fritzing, en el cuál, vamos a tener que montar las piezas electrónicas en la protoboard, para la cual vamos a utilizar el siguiente material:
- 1 protoboard
- 1 batería de 9 volts
- 1 switch
- 1 circuito integrado de compuerta AND de dos entradas 7408:
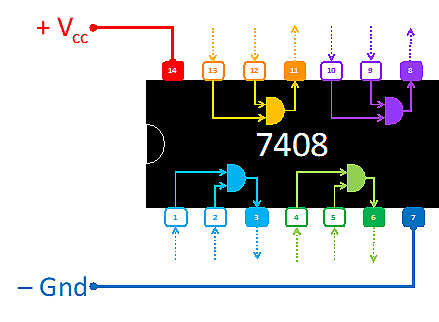
- 1 led
- Cables de conexión
Solución:
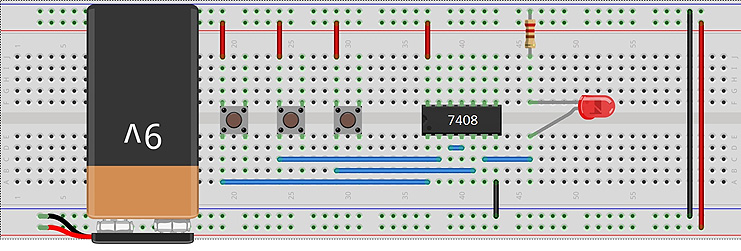

Revisa el siguiente recurso Compuerta AND de tres entradas utilizando un circuito integrado 7408 .
Implementación de una compuerta XOR con AND, OR y NOT
I. Planteamiento del problema
La implementación de una compuerta XOR basándose en compuertas AND y OR es una forma de mostrar cómo se pueden crear estructuras digitales a partir de las compuertas básicas, la compuerta XOR, también conocida como “OR exclusiva”, su expresión Booleana es una suma binaria de un dígito cada uno y el resultado obtenido será la salida. La salida tiene un estado activo “1” al tener las entradas en estados diferentes (una activa y otra inactiva).
En un diagrama esquemático quedaría:

II. Tabla de verdad
La tabla de verdad de la función XOR es:
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
III. Obtención de la función booleana
La expresión booleana que representa la función XOR es: $S=A \oplus B=AB'+A'B$
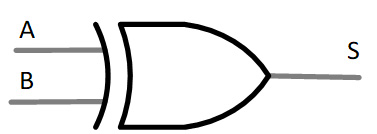
Por lo que la simplificación de la función booleana para la implementación con compuertas AND y OR de 2 entradas para la compuerta XOR, es la misma expresión $S=A \oplus B=AB'+A'B$ y su símbolo para la compuesta XOR:
IV. Diagrama del diseño lógico
El diagrama lógico para esta implementación se muestra en la siguiente figura, se realizó de acuerdo a la función que tenemos para la salida (S), con sus entradas A y B.
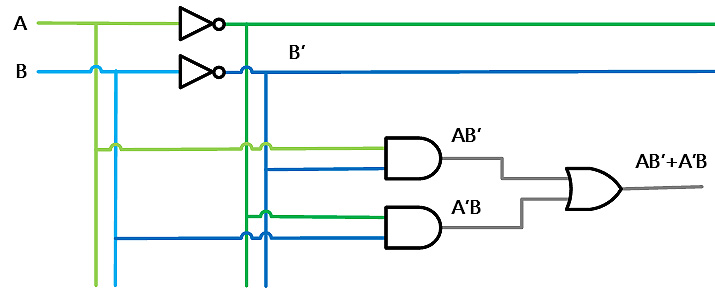
Y puede comprobarse que: $S=A \oplus B=AB’+A’B$
V. Construcción o simulación del circuito lógico
Para hacer el arreglo vamos a utilizar el software Fritzing, en el cuál, vamos a tener que montar las piezas electrónicas en la protoboard, para la cual vamos a utilizar el siguiente material:
- 1 protoboard
- 1 batería de 9 volts
- 2 switch
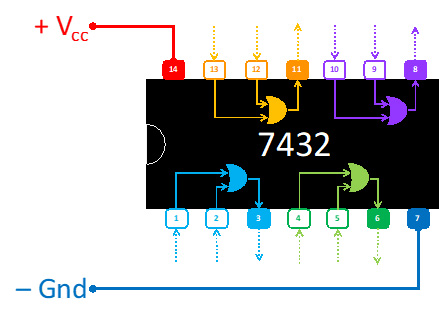
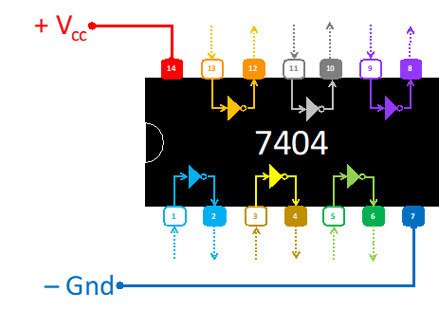
- 3 circuitos integrados: 1) AND de dos entradas 7408, 2) AND de dos entradas 7432, 3) NOT 7404

- 1 led
- Cables de conexión
Solución:


Revisa el siguiente recurso Compuerta XOR con compuertas AND y OR de 2 entradas .
Ahora revisa los ejemplos 3 y 4 (abajo) y resuelve los ejercicios
Ejemplo 3 (con ejercicios)
Semisumador
I. Planteamiento del problema
Las computadoras digitales realizan una variedad de tareas de procesamiento de información. Entre las funciones básicas encontradas están las diversas operaciones aritméticas. Sin duda, la operación aritmética más básica es la adición de dos dígitos binarios. Esta adición simple consta de cuatro operaciones elementales posibles, a saber: 0+0=0, 0+1=1, 1+0=1, 1+1=10. Las primeras tres operaciones producen una suma cuya longitud es un dígito, pero cuando los bits sumandos dan como resultado 10, la suma binaria consta de dos dígitos. El bit significativo más alto de este resultado se denomina acarreo. Un circuito combinacional que lleva a cabo la adición de dos bits se denomina medio sumador. Uno que lleva a cabo la adición de tres bits (dos bits significativos y una cuenta que se lleva previa) es un sumador completo. El nombre del primero proviene del hecho de que dos medios sumadores se emplean para implementar un sumador completo.
De lo anterior, sabemos entonces que el circuito para el medio sumador requiere dos entradas binarias y dos salidas binarias. Las variables de entrada designan los bits sumando; las variables de salida producen la suma y el acarreo. Es necesario especificar dos variables de salida debido a que el resultado puede constar de dos dígitos binarios. Se asignan de forma arbitraria los símbolos x e y a las dos entradas y S (de suma) y C (para el acarreo), a las salidas.
Por lo que el semisumador es la suma de dos números binarios de 1 bit y como resultado es la suma de los dos bits más el acarreo (carry).
En un diagrama esquemático quedaría:

II. Tabla de verdad
Ahora que se han establecido el número y nombres de las variables de entrada y salida, ya puede formularse la tabla de verdad para identificar en forma exacta la función del medio sumador. Esta tabla de verdad se muestra a continuación:
| x | y | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
III. Obtención de las funciones booleanas
Vamos a crear una tabla de verdad de $2^n$ en donde n es el número de variables en este caso 2 es el número de variables de la función, por lo que tendremos una tabla de $2^2=4$ cuadros:
Completa la tabla colocando la información que falta.
Salida S. Resultado de la suma
| Identificando la primera aproximación por mintérminos | |
| Ubicándolos en el mapa de Karnaugh: | |
| En este punto no hay nada que agrupar, por lo que: | |
| Que corresponde a una compuerta XOR |
$$S=x \oplus y$$

|
Salida C. Acarreo de la suma
| Identificando la primera aproximación por mintérminos | |
| Ubicándolos en el mapa de Karnaugh: | |
| En este punto no hay nada que agrupar, por lo que: | |
| Que corresponde a una compuerta XOR |
$$C=x \cdot y$$

|
Por lo tanto, se han obtenido las dos funciones de salida una para la suma, y otra para el acarreo: $$S=x \oplus y$$ $$C=x \cdot y$$
IV. Diagrama del diseño lógico
El diagrama lógico para esta implementación se muestra en la siguiente figura, la implementación se realizó de acuerdo a las funciones que tenemos para la suma (S) y para el acarreo (C).
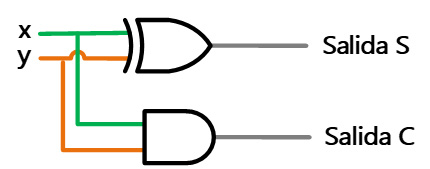
V. Construcción o simulación del circuito lógico
Para hacer el arreglo vamos a utilizar el software Fritzing, en el cuál vamos a montar las piezas electrónicas en la protoboard utilizando el siguiente material:
- 1 protoboard
- 1 batería de 9 volts
- 2 switch
- 2 circuitos integrados: 1) AND de dos entradas 7408 y 2) XOR de dos entradas 7486
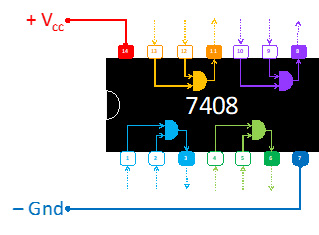
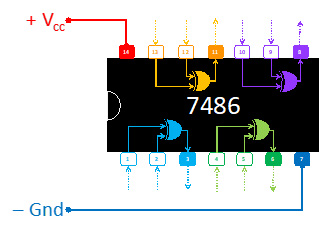
- 1 led
- Cables de conexión
Solución:


Revisa el siguiente recurso Semisumador .
Ejemplo 4 (con ejercicios)
Sumador completo de un bit
I. Planteamiento del problema
El sumador es un circuito digital que realiza la suma de números binarios. En las computadoras dentro del microprocesador se utilizan sumadores en las unidades aritméticas lógicas (ALU) para realizar las operaciones. En otras partes del procesamiento de la información dentro de la computadora, se utilizan para el cálculo de direcciones, en la búsqueda de los índices de tablas y en operaciones de incremento o decremento.
El sumador completo de un bit es el arreglo digital que trabaja, si por cada par de sumandos binarios puede producir un bit de acarreo, también debe tener la capacidad de reconocer cuando viene un bit de acarreo del sumador de nivel inferior (es decir que cuando en el sistema decimal, decimos un llevo algo, debido a la suma de las unidades, hay que pasar a las decenas).
Un sumador completo de 1 bit, es un circuito con 3 entradas y 2 salidas. Las tres entradas son: un acarreo de entrada (C), y los dos bits que vamos a sumar (A y B).
Si cada par de sumandos binarios se produce un resultado de la suma (R) y un bit de acarreo (K), también debe tener la capacidad de reconocer cuando viene un bit de acarreo del sumador de nivel inferior.

II. Tabla de verdad
Ahora que se han establecido el número y nombres de las variables de entrada y salida, ya puede formularse la tabla de verdad para identificar en forma exacta la función del sumador completo.
Llena los espacios para completar el proceso de construcción de la solución.
Vamos a entender la tabla:
| Entradas | Salidas | |||
|---|---|---|---|---|
| A | B | C | Acarreo (K) | Suma (R) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
III. Obtención de las funciones booleanas
Salida R
Vamos a crear una tabla de verdad ordenando los valores de entrada A, B y C, con los de la salida R nos queda:
| A | B | C | R | Mintérmino |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | A’B’C’ |
| 0 | 0 | 1 | 1 | A’B’C |
| 0 | 1 | 0 | 1 | A’BC’ |
| 0 | 1 | 1 | 0 | A’BC |
| 1 | 0 | 0 | 1 | AB’C’ |
| 1 | 0 | 1 | 0 | AB’C |
| 1 | 1 | 0 | 0 | ABC’ |
| 1 | 1 | 1 | 1 | ABC |
Sumamos los mintérminos donde la salida R=1:
Observa la tabla de verdad y completa en el recuadro el término que corresponde:
Realizando las manipulaciones algebraicas:
Simplificación Algebraica
Simplificación por mapas de Karnaugh:
Marcamos los mintérminos en la tabla que se van a emplear para generar la función:
| A | B | C | R | Mintérmino |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | A’B’C’ |
| 0 | 0 | 1 | 0 | A’B’C |
| 0 | 1 | 0 | 1 | A’BC’ |
| 0 | 1 | 1 | 0 | A’BC |
| 1 | 0 | 0 | 1 | AB’C’ |
| 1 | 0 | 1 | 0 | AB’C |
| 1 | 1 | 0 | 0 | ABC’ |
| 1 | 1 | 1 | 1 | ABC |
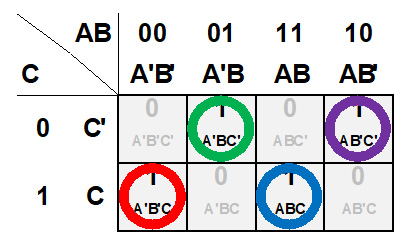
A partir del mapa de karnaugh y de las agrupaciones propuestas, el circuito equivalente sería el que se presenta a continuación:
Observa el mapa de Karnaugh y completa en el recuadro el término que corresponde:
Como pudo verse, el mapa de Karnaugh no ofrece alguna forma de simplificación. Dado que no podemos realizar ninguna agrupación por rectángulos con un número elementos que sea potencia de dos (2, 4, 8, 16, …), el resultado sólo se expresa en mintérminos (sin simplificación).
Las agrupaciones que se obtuvieron por álgebra previamente equivalen a:
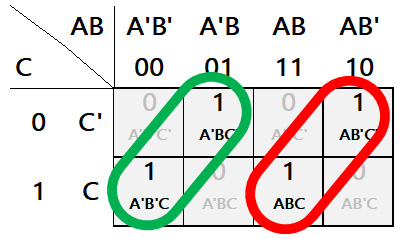
Observa el mapa de Karnaugh y completa en el recuadro el término que corresponde:
Simplificando:
R = A'(B’C + BC’) + A(BC+B’C’)
R = A’(B⊕C) + A(B⊕C)'
R = A⊕(B⊕C)
Salida K
Recuerda que la salida es 1 cuando la cuenta o suma de unos es igual a 2 o 3:
Completa los espacios y presiona Verificar para comparar tus respuestas y continuar con el procedimiento:
La primera aproximación de función, como suma de mitérminos:
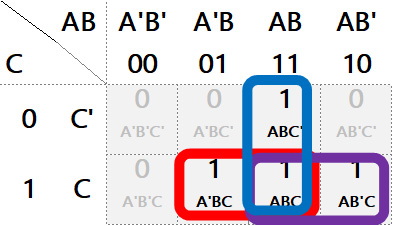
Completa la función para K = AB + AC + BC
Una simplificación algebraica por la propiedad de distributividad respecto a C:
K = AB + (A+B)C
Por lo que las funciones booleanas para las salidas son:
| Resultado | $R=A \oplus (B \oplus C)$ |
|---|---|
| Acarreo | $K=AB+(A+B)C$ |
IV. Diagrama del diseño lógico
El diagrama lógico para esta implementación se muestra en la siguiente figura, la implementación se realizó de acuerdo a las funciones que tenemos para la suma (R) y para el acarreo (K).
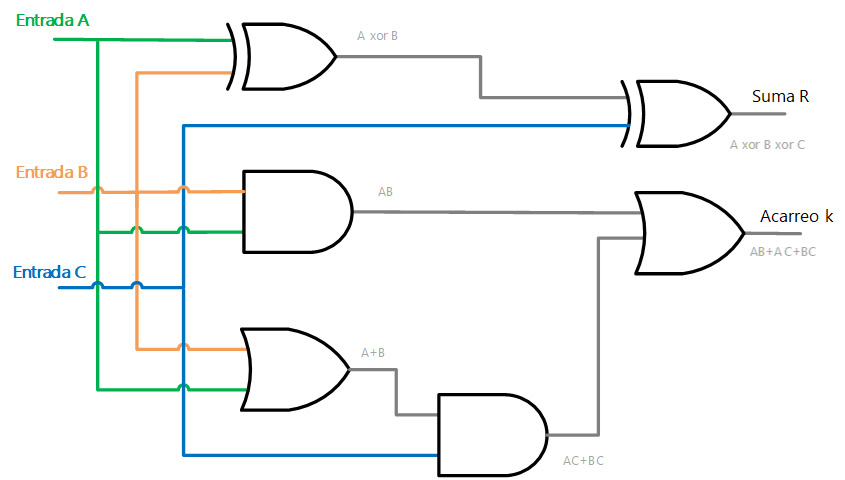
V. Construcción o simulación del circuito lógico
Para hacer el arreglo vamos a utilizar el software Fritzing, en el cuál vamos a montar las piezas electrónicas en la protoboard, utilizando el siguiente material:
- 1 protoboard
- 1 batería de 9 volts
- 3 switch
- 3 circuitos integrados: 1) AND de dos entradas 7408, 2) OR de dos entradas 7432 y 3) XOR de dos entradas 7486



- 1 led
- Cables de conexión
Implementación:
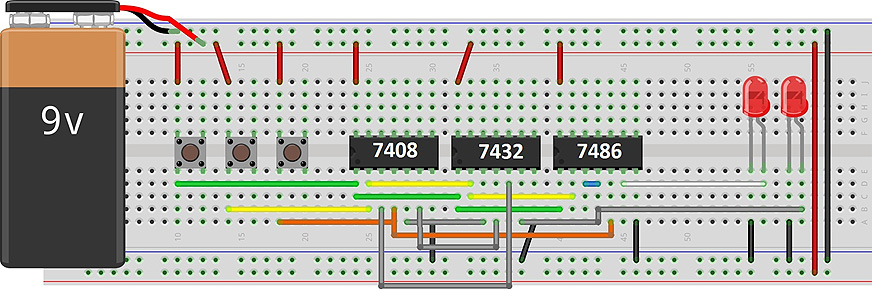

Revisa el siguiente recurso Sumador completo de un bit .


