En el ejemplo anterior, el crecimiento bacteriano se representó mediante una función exponencial de base 2. No obstante, existen diversos fenómenos asociados a las ciencias y a las ingenierías cuyos modelos de crecimiento y decrecimiento se expresan mediante funciones exponenciales de base e; donde $e$ es un número irracional trascendente cuyas primeras cifras decimales son 2.71828182. En 1683 el matemático Jacob Bernoulli encontró una primera aproximación para $e$ mientras examinaba un problema de interés compuesto; sin embargo, dicho número fue introducido en el lenguaje matemático por Leonhard Euler (1707-1783); y por ello se le conoce como número de Euler (Bocco, 115).
El llamado número de Euler o número $e$ es un número irracional trascendente cuyas primeras cifras decimales son 2.71828182, y que determina la base para la llamada función exponencial natural:
$f\left( x \right) = {e^x}$
Fórmula 4
A continuación, analizarás un problema de interés compuesto que te permitirá determinar al número de Euler o número $e$, y analizarás diversos casos de interés para determinar el tipo de inversión más conveniente. Finalmente, a partir de un caso de inversión límite, determinarás una fórmula exponencial de base $e$ para calcular el capital acumulado.

Se denomina interés compuesto cuando se tiene una inversión donde los intereses se capitalizan, es decir, se acumulan al capital principal para dar lugar a un nuevo capital, el cual se reinvierte sucesivamente en el siguiente periodo hasta concluir el plazo de inversión. También existe el interés simple cuando se tiene una inversión donde el capital principal no varía durante el tiempo que dura la operación.
Interés compuesto
Si se invierte una cantidad de dinero o capital principal $P$ con una tasa de interés $i$ por periodo; entonces, el capital acumulado $A$ al final de un periodo será igual a la suma del capital principal y la utilidad generada en un periodo, es decir: $$A = P + P \cdot i$$ donde $P \cdot i$ es la utilidad obtenida en el periodo.
Al factorizar la expresión anterior se tiene que el capital acumulado es:
$A = P\left( {1 + i} \right)$
Fórmula 5

Si se invierte un capital principal $P$ de 100,000 al plazo de un año con una tasa de interés $i$ del 12% por periodo anual ¿Cuál es capital acumulado al final del periodo? Selecciona la opción correcta.
- A = $110,000
- A = $112,000
- A = $120,000
Para calcular el capital acumulado al final del periodo se emplea la fórmula 5:
$\eqalign{ & A = 100,000\left( {1 + 0.12} \right) \cr & A = 112,000 \cr} $
donde $P = 100,000$ e $i = 0.12$.
Si se invierte una cantidad de dinero o capital principal $P$ con una tasa de interés $i$ por periodo; entonces, el capital acumulado $A$ al final de un periodo será igual a la suma del capital principal y la utilidad generada en un periodo, es decir: $$A = P + P \cdot i$$ donde $P \cdot i$ es la utilidad obtenida en el periodo.

Si se reinvierte el capital acumulado en un segundo periodo, entonces el nuevo capital principal es $P\left( {1 + i} \right)$. De forma análoga al primer periodo, el capital acumulado A se obtiene al multiplicar el capital principal $P\left( {1 + i} \right)$ por el factor $\left( {1 + i} \right)$; en consecuencia, el nuevo capital acumulado al término del segundo periodo está dado por:
$A = P\left( {1 + i} \right)\left( {1 + i} \right) = P{\left( {1 + i} \right)^2}$
Fórmula 6
Si se invierte un capital principal $P$ de 100,000 al plazo de dos años con una tasa de interés $i$ del 12% por periodo anual. ¿Cuál es el capital acumulado al final del segundo periodo? Selecciona la opción correcta.
- A = $125,440
- A = $127,000
- A = $132,200
Para calcular el capital acumulado al final del segundo periodo se emplea la fórmula 6:
$\eqalign{ & A = 100,000{\left( {1 + 0.12} \right)^2} \cr & A = 125,440 \cr} $
donde $P = 100,000$ e $i = 0.12$

Si nuevamente se reinvierte el capital acumulado por un tercer periodo, el nuevo capital principal es $P{\left( {1 + i} \right)^2}$ y el nuevo capital acumulado $A$ se obtiene al multiplicar el capital principal $P{\left( {1 + i} \right)^2}$ por el factor $\left( {1 + i} \right)$. Entonces, el capital acumulado es:
$A = P{\left( {1 + i} \right)^2}\left( {1 + i} \right) = P{\left( {1 + i} \right)^3}$
Fórmula 7
Si se invierte un capital principal $P$ de 100,000 al plazo de tres años con una tasa de interés $i$ del 12% por periodo anual ¿Cuál es el capital acumulado al final del tercer periodo? Selecciona la opción correcta.
- A = $125,440.0
- A = $140,492.8
- A = $157351.9
Para calcular el capital acumulado al final del segundo periodo se emplea la fórmula 7:
$\eqalign{ & A = 100,000{\left( {1 + 0.12} \right)^3} \cr & A = 140,492.8 \cr} $
donde $P = 100,000$ e $i = 0.12$

Las fórmulas 5 a 7 permiten deducir que el capital acumulado para un cuarto y quinto periodos estarían dados por $P{\left( {1 + i} \right)^4}$ y $P{\left( {1 + i} \right)^5}$, respectivamente.
A partir de la deducción anterior, determina es el capital acumulado después de $k$ periodos. Selecciona la opción correcta.
- $A = P{\left( {1 + i} \right)^{k - 1}}$
- $A = P{\left( {1 + i} \right)^k}$
- $A = P{\left( {1 + i} \right)^{k + 1}}$
El capital acumulado después de k periodos está dado por:
$A = P{\left( {1 + i} \right)^k}$
Si se invierte un capital inicial $P$ a una tasa de interés $i$ por periodo; entonces, el capital acumulado $A$ después de $k$ periodos es:
$A = P{\left( {1 + i} \right)^k}$
Fórmula 8
donde $A$ es una función exponencial de base $1 + i$; $i$ es la tasa se interés por periodo; $k$ es el número de periodos.

Si se invierte un capital principal $P$ de 100,000 al plazo de 11 años con una tasa de interés $i$ del 12% por periodo anual. ¿Cuál es el capital acumulado al final del onceavo periodo? Selecciona la opción correcta.
- A = $277,307.9
- A = $310,584.8
- A = $347,855
Para calcular el capital acumulado se emplea la fórmula 8; para el onceavo periodo se tiene que $k = 11$, entonces
$\eqalign{ & A = 100,000{\left( {1 + 0.12} \right)^{11}} \cr & A = 347,855 \cr} $
donde $P = 100,000$ e $i = 0.12$

Si se invierte el capital principal $P$ durante $t$ años, con una tasa de interés anual $r$ y el interés se capitaliza $n$ veces por año; entonces, la tasa de interés en cada periodo es:
$i = \frac{r}{n}$
Fórmula 9
Y el número de periodos está dado por:
$k = n \cdot t$
Fórmula 10
Al sustituir las fórmulas 9 y 10 en 8, se determina la fórmula para el interés compuesto.
$A\left( t \right) = P{\left( {1 + \frac{r}{n}} \right)^{n \cdot t}}$
Fórmula 11
donde $A\left( t \right)$ es el capital acumulado después de $t$ años; $P$ es el capital principal; $r$ es la tasa de interés anual; $n$ es el número de veces que el interés se capitaliza por año.
Ejemplo
Si se invierte un capital principal de $100,000 al plazo de 5 años con una tasa de interés anual del 12% ¿Cuál es el capital acumulado si el interés se capitaliza semestralmente?
Para calcular el capital acumulado se emplea la fórmula 11; considerando $P = 100,000$, $r = 0.12$, $n = 2$ y $t = 5$
$\eqalign{ & A\left( 5 \right) = 100,000{\left( {1 + \frac{{0.12}}{2}} \right)^{2\left( 5 \right)}} \cr & A\left( 5 \right) = 179,084.77 \cr} $
Se considera que $n = 2$ puesto que hay dos semestres por año.
Si se invierte un capital principal de 100,000 al plazo de 5 años con una tasa de interés anual del 12% ¿Cuál es el capital acumulado si el interés se capitaliza de forma anual, semestral, trimestral, mensual y diario? Relaciona las columnas.

Una inversión capitalizable de forma continua implica que $n$ tiende a infinito; es decir:
$A\left( t \right) = {\lim _{n \to \infty }}P{\left( {1 + \frac{r}{n}} \right)^{n \cdot t}}$
Al aplicar las propiedades de los límites, se tiene que:
$A\left( t \right) = {\lim _{n \to \infty }}P{\left( {1 + \frac{r}{n}} \right)^{n \cdot t}} = {\lim _{n \to \infty }}P \cdot {\lim _{n \to \infty }}{\left( {1 + \frac{r}{n}} \right)^{n \cdot t}}$
Entonces $$A\left( t \right) = P \cdot {\lim _{n \to \infty }}{\left( {1 + \frac{r}{n}} \right)^{n \cdot t}}$$
Fórmula 12
Si consideramos que $x = \frac{n}{r}$, entonces
$\frac{1}{x} = \frac{r}{n}$ y $n = xr$
Al sustituir las dos igualdades anteriores en la fórmula 12, se tiene que
$A\left( t \right) = P \cdot {\lim _{x \to \infty }}{\left( {1 + \frac{1}{x}} \right)^{xrt}} = P \cdot {\lim _{x \to \infty }}{\left( {{{\left( {1 + \frac{1}{x}} \right)}^x}} \right)^{rt}}$
$A\left( t \right) = P \cdot {\left( {{{\lim }_{x \to \infty }}{{\left( {1 + \frac{1}{x}} \right)}^x}} \right)^{rt}}$
Fórmula 13
En la fórmula 13 se tiene que determinar el valor de ${\lim _{x \to \infty }}{\left( {1 + \frac{1}{x}} \right)^x}$
Para determinar un valor aproximado de ${\lim _{x \to \infty }}{\left( {1 + \frac{1}{x}} \right)^x}$, completa y analiza la siguiente tabla. Indica los valores faltantes con 9 cifras después del punto decimal.

La gráfica de ${\left( {1 + \frac{1}{x}} \right)^x}$ para diferentes valores de x mayores a 1 es la siguiente:
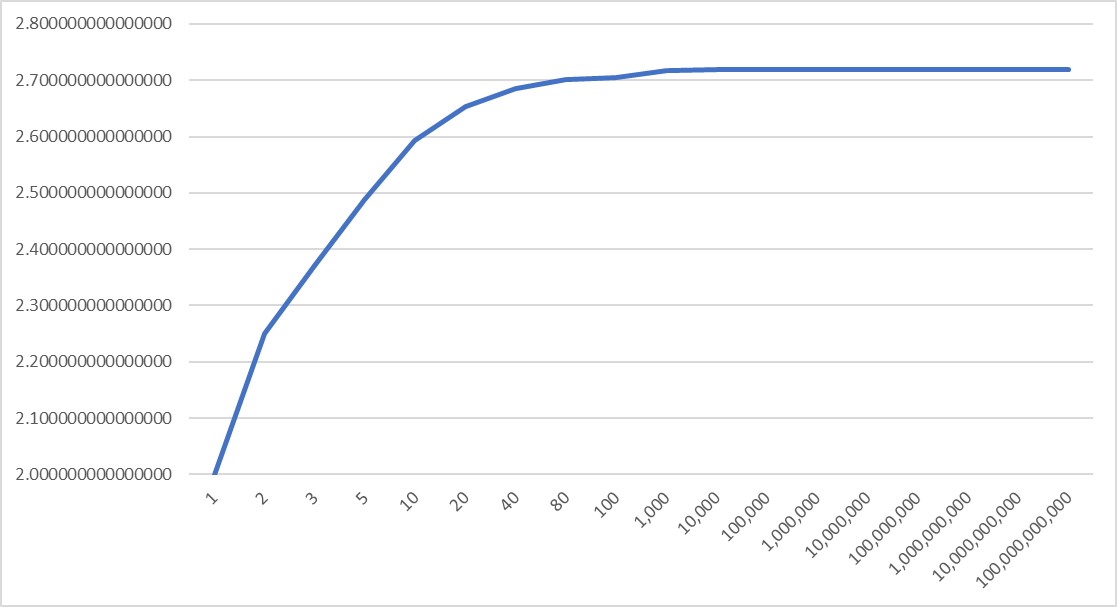

Como puedes observar, la gráfica muestra la existencia de un valor límite: conforme se incrementa el valor de x , el valor de la función tiende a un número cuyos primeros dígitos son 2.71828, el cual no puede calcularse con precisión por ser un número irracional ¿Sabes qué número es?
El número al cual tiende el límite ${\lim _{x \to \infty }}{\left( {1 + \frac{1}{x}} \right)^x}$ se denota por la letra $e$ y es conocido como número de Euler.


Por lo tanto, dado que ${\lim _{x \to \infty }}{\left( {1 + \frac{1}{x}} \right)^x} = e$ se tiene que
$A\left( t \right) = P \cdot {\left( {{{\lim }_{x \to \infty }}{{\left( {1 + \frac{1}{x}} \right)}^x}} \right)^{rt}} = P \cdot {\left( e \right)^{rt}}$
$A\left( t \right) = P \cdot {e^{rt}}$
Fórmula 14
donde $A\left( t \right)$ es el capital acumulado después de $t$ años en una inversión capitalizable de forma continua; $P$ es el capital principal; $r$ es la tasa de interés anual; y $t$ es el tiempo de capitalización. Observa que $A\left( t \right)$ es una función exponencial de base e, y describe el crecimiento continuo del capital acumulado en un problema de interés compuesto.
A partir de la fórmula 14, es posible determinar una expresión para el capital acumulado en función del tiempo $t$, siendo conocidos el capital principal $P$ y la tasa de interés $r$. Por ejemplo, si se invierte un capital principal de 100,000 al plazo de $t$ años con una tasa de interés anual del 12%. Selecciona la fórmula para calcular el capital acumulado en función del tiempo dado, si el interés se capitaliza de forma continua.
- $A\left( t \right) = 10,000{e^{0.12t}}$
- $A\left( t \right) = 0.12{e^{100,000t}}$
- $A\left( t \right) = t \cdot {e^{0.12\left( {10,000} \right)}}$
El capital acumulado en función del tiempo t , cuando se invierte un capital principal de $100,000 con una tasa de interés anual del 12% está dado por:
$A\left( t \right) = 10,000{e^{0.12t}}$
donde $P = 100,000$ y $r = 0.12$
Si se invierte un capital principal de 100,000 al plazo de 5 años con una tasa de interés anual del 12% ¿Cuál es el capital acumulado si el interés se capitaliza de forma continua? Selecciona la opción correcta.
- A(5) = $181,669.67
- A(5) = $182,193.91
- A(5) = $182,211.88
Utilizando la fórmula 14 se obtiene que el capital acumulado de forma continua es:
$A\left( 5 \right) = 100,000 \cdot {e^{0.12\left( 5 \right)}} = 182,211.88$
donde $P = 100,000$, $r = 0.12$ y $t = 5$
Como pudiste observar, la fórmula $A\left( t \right) = 10,000{e^{0.12t}}$ te permite calcular el capital acumulado de forma continua en determinado tiempo; pero también te permite calcular el tiempo que debe transcurrir para tener un determinado capital acumulado ¿Sabes cómo hacerlo?

¿Cuánto tiempo tengo que mantener una inversión para tener un capital acumulado de $200,000? Selecciona la opción correcta.
- t = 5.58 años
- t = 5.78 años
- t = 5.98 años
Si el capital acumulado es de $200,000 entonces:
$A\left( t \right) = 100,000 \cdot {e^{0.12\left( t \right)}} = 200,000$
Se despeja el tiempo t utilizando las propiedades de los logaritmos naturales, es decir:
$100,000 \cdot {e^{0.12\left( t \right)}} = 200,000$
${e^{0.12\left( t \right)}} = \frac{{200,000}}{{100,000}} = 2$
$\ln \left( {{e^{0.12\left( t \right)}}} \right) = \ln 2$
$0.12\left( t \right) = \ln 2$
$t = \frac{{\ln 2}}{{0.12}}$
$t = 5.78$
¿Cómo determinarías la rapidez instantánea del capital acumulado cuando han transcurrido 5.78 años? Selecciona la opción correcta.
- Evaluar el tiempo indicado en $A\left( t \right) = 10,000{e^{0.12t}}$ y derivar el resultado.
- Derivar la función para el crecimiento exponencial $A\left( t \right) = 10,000{e^{0.12t}}$ y evaluar en el tiempo indicado.
- No es posible calcular la rapidez instantánea del capital acumulado.
Para determinar la rapidez instantánea del capital acumulado se requiere calcular la derivada de la función, es decir, $A'\left( t \right) = \frac{d}{{dt}}\left( {10,000{e^{0.12t}}} \right)$ y evaluarla en el tiempo requerido; recuerda que la derivada de una función proporciona la razón de cambio o rapidez instantánea con la que cambia una variable respecto a otra.