III. Identificación de los puntos problemáticos y propuestas de solución

 Generalidades sobre los errores al operar con números

Ya sea que en nuestros cursos trabajemos utilizando la aritmética generalizada para tender el puente con el álgebra, partiendo del estudio de métodos para resolver problemas, o como lenguaje funcional que incluye el estudio de relaciones entre cantidades, además de tratarla como estructura lógico-conceptual, es decir, con todos estos abordajes a la vez, que es lo ideal, que deberían estar contemplados en cualquier plan de estudios del nivel bachillerato. Los errores en los que incurren nuestros estudiantes son poco más o menos del tipo de los que aquí mostramos y cuyo análisis nos conduce a afirmar que muchos de ellos son atribuibles a una o varias de las situaciones siguientes: 

1. La incomprensión e incorrección del cálculo aritmético por parte de los estudiantes.
2. El uso inapropiado de fórmulas y procedimientos “recetas de cocina”.
3. Los objetivos de las actividades matemáticas y la naturaleza de las respuestas en la aritmética y el álgebra básica.
4. La naturaleza y significado de los términos, símbolos y letras en la aritmética, álgebra básica y geometría en contraste con el lenguaje cotidiano y la aritmética conocida.

 Para efectos de síntesis sobre la problemática en la enseñanza-aprendizaje del número y sus operaciones básicas, retomamos los errores que se generan en el desarrollo conceptual durante la transición de la aritmética al álgebra y hacemos notar que tienen mucho que ver con los tres primeros aspectos mencionados en la lista anterior. El primero de la lista tiene más bien que ver con hábitos de aprendizaje memorísticos mezclados con generalizaciones equivocadas sobre las funciones que cumplen los operadores y/o las cantidades numéricas. Pasaremos ahora a sintetizar los hallazgos más relevantes de los errores que cometen los estudiantes y que tienen sus bases en sus concepciones en torno a la aritmética, el álgebra y el uso del lenguaje materno, adquiridas en sus cursos anteriores a su ingreso a la universidad.

 

1. La incomprensión e incorrección del cálculo aritmético por parte de los estudiantes

Las incomprensiones sobre la aritmética por parte de los estudiantes son fuente de confusiones en álgebra ya que el aprendizaje del  álgebra debe comenzar con buenas bases de la aritmética generalizada. En la escuela primaria se debe hacer énfasis en la comprensión de los procesos y la generalización de las relaciones desde el cálculo y razonamiento numérico, ya que en el aprendizaje del álgebra se requiere que los principios y propiedades de las estructuras matemáticas hayan sido asimilados primero dentro del contexto aritmético. En muchas ocasiones, las dificultades de los estudiantes en el álgebra son parte de su incomprensión de la aritmética. Muchos estudiantes fueron promovidos a los grados superiores sin corregir comprensiones y procesos de cálculo incorrectos, como en el caso de los números racionales, las potencias, el uso de los paréntesis y el manejo de los signos. Entre el profesorado ya no causa sorpresa encontrar escrito por algunos alumnos los resultados de operaciones con números racionales como estos:

que luego trasladan tal cual al álgebra siguiendo su lógica personal.

También son frecuentes los errores al calcular incorrectamente el mínimo común denominador o en la obtención de fracciones equivalentes, por ejemplo, al sumar 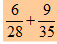  hacen cálculos y escriben cosas como  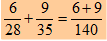sin transformar cada fracción en su equivalente, en otras ocasiones, preocupados por los factores de expansión, no multiplican por los numeradores y en consecuencia tampoco los convierten a las fracciones equivalentes como en este ejemplo  al sumar  ,

hacen cálculos y escriben cosas como      sin transformar cada fracción en su equivalente, en otras ocasiones, preocupados por los factores de expansión, no multiplican por los numeradores y en consecuencia tampoco los convierten a las fracciones equivalentes como en este ejemplo    .

La dificultad de la comprensión y manejo de los números racionales tienen como base, entre otras, que el número racional implica una relación entre dos números     y que admite múltiples interpretaciones, puesto que puede modelar una amplia variedad de situaciones. También existe al menos otro factor que dificulta el aprendizaje y enseñanza de las fracciones: sus propiedades son distintas a las de los números naturales. Por ejemplo, no existe el antecesor y sucesor de un número racional, siempre será posible ubicar una fracción entre otras dos; la regla, según la cual al multiplicar dos números siempre se obtendrá uno mayor o al dividir se obtendrá uno menor tampoco se cumple en los racionales. Las diferencias entre uno y otro conjunto numérico, según según han documentado nuestras investigaciones (Flores, Medina y Peralta. 2016), son fuente importante de obstáculos y dificultades en el aprendizaje.

Cuando operan con el signo «–» que va delante de un paréntesis o en una fracción compleja, cometen errores, como:      y    falta de percepción e interiorización de conceptos matemáticos que se estudian en la aritmética se refleja en los errores que los estudiantes cometen al operar con números o literales, como por ejemplo, cuando multiplican 3×2 en expresiones como 3² en lugar de 3×3, de aquí derivan muchas generalizaciones incorrectas para el álgebra.

  B) El uso inapropiado de «fórmulas» o «procedimientos» “recetas de cocina”

Los alumnos tienden a memorizar las fórmulas y procedimientos que han tomado de sus clases o libros de texto y las aplican a cuanto problema se enfrentan, convirtiéndolas en prototipos de resolución matemática que aplican tal cual, sin discriminar si dicha aplicación es pertinente o no; también sucede que en situaciones donde el prototipo no encaja, les hacen adecuaciones con el afán de «adaptarlas» a nuevas situaciones. De esta manera construyen un vínculo que liga y salva el espacio entre procedimientos conocidos y problemas nuevos, lo que origina errores debido a las falsas generalizaciones sobre los operadores y los números que acostumbran a usar.

Dentro de estos procedimientos prototipo, hay errores que provienen de una incorrecta aplicación del concepto de linealidad de los operadores y, en consecuencia, una falsa generalización, por ejemplo, en las expresiones ( ab )² y (a + b )^2, el exponente opera linealmente en la primera, distribuyéndose en cada uno de los factores del producto, es decir, (ab) ² = a²b²; por lo que para el alumno, lo más lógico y sencillo es suponer que también se cumple que (a + b ) ² = a² + b², sin percatarse de que aquí, la linealidad no siempre funciona, puesto que la potencia de una suma no es la suma de las potencias, un problema que refuerza esta generalización falsa es que los estudiantes llegan a encontrar algunos pares de valores que verifican la igualdad, y entonces dicen que han “comprobado” la veracidad de las igualdades para todos los valores y “hacen ley” la linealidad de las potencias en sumas y productos por igual.

Aplicar la linealidad resulta muy natural entre los alumnos dado que están familiarizados con ella en experiencias anteriores. Derivados de esta situación, en nuestra investigación arriba citada, hemos constatado las hipótesis acerca de los errores más frecuentes que cometen los estudiantes durante su aprendizaje del álgebra y que podemos resumir como sigue:

1. Errores relacionados con el mal uso de la ley distributiva.
2. Errores debidos al uso inadecuado de los inversos.
3. Errores por mal uso de las reglas de cancelación.
4. Errores derivados de falsas generalizaciones sobre números.
5. Errores por el abuso de métodos no-formales por parte de los alumnos.

Ejemplificaremos uno de ellos.

 Errores por el abuso de métodos no-formales por parte de los alumnos

El anclaje del pensamiento en métodos de resolución personal hace que los estudiantes no utilicen métodos matemáticos formales para resolver problemas y, en consecuencia, sus habilidades para la representación simbólica de elementos y procedimientos los conduce a plantear generalizaciones incompletas o erróneas. El hecho de que los alumnos permanezcan fieles a sus propios métodos es porque éstos parecen tener éxito en situaciones sencillas, pero en el momento en que se requiere que dichos métodos les funcionen en problemas más complejos en el álgebra, las extensiones que propone el alumno resultan inadecuadas ya que carece de habilidades para elaborar y comprender enunciados matemáticos generales. Así, por ejemplo, si al aprendiz le planteamos situaciones como:

5 + 6 = 11 7 + 8 = 15   y, en general, la suma de dos números enteros consecutivos es:   Respuesta:   n + 1  Son capaces de calcular la solución de las sumas parciales, pero no son competentes para hallar un modelo matemático general que describa simbólicamente la situación, es decir, que reconozcan que la suma de dos números enteros consecutivos cualesquiera es el doble del menor más uno, en símbolos: 2n + 1.
Dividir 24 en dos partes, una parte es 9, halla la otra parte:  Respuesta:   15	Este tipo de situaciones son resueltas por los estudiantes de manera numérica buscando dos valores que satisfagan las condiciones, esto es, calculan la diferencia entre 24 y 9.

 

 C) Los objetivos de las actividades matemáticas y la naturaleza de las respuestas en álgebra

El objetivo central del alumno en la aritmética es buscar soluciones numéricas correctas, para ello, está acostumbrado a poner toda su atención en la tarea de hallar un número como solución al problema y resulta que en álgebra esto ya no es así, en álgebra los objetivos son diferentes, los propósitos fundamentales son la identificación de «objetos generales» con sus atributos y valores, la determinación de las relaciones entre dichos objetos y los procesos involucrados en su uso o aplicación concreta a problemas que se materializan en la formulación de expresiones generales simplificadas (modelos matemáticos) que permiten hallar soluciones numéricas particulares, sin que esto sea el objetivo principal. Sin embargo, muchos estudiantes tienen la atención puesta en encontrar un número como respuesta y suponen que en álgebra, al igual que en aritmética, se les pide “siempre” una solución numérica, que además, ha de ser única, la explicitación de que tanto el proceso de análisis, como la interpretación de la solución en el problema y la posibilidad de varias soluciones, son el foco principal de atención, los desconcierta.

Esta idea de la respuesta única es una de las causas de errores típicos cometidos con frecuencia, —como hemos visto durante nuestra experiencia docente, en las entrevistas y registros escritos por los estudiantes en nuestra investigación (Flores, Medina y Peralta 2016)—, por alumnos que simplifican la expresión 5x + 2y en 7xy. Los estudiantes lidian con este problema porque no aceptan fácilmente que no haya cerradura en una suma —siempre se puede sumar ¿o no?— se confunden ante la posibilidad de dejar indicada la operación y que, además, la expresión toda exprese un sólo objeto matemático; también sucede que contestan de acuerdo con el formato aritmético y escriben lo que se supone debe ser una «respuesta correcta».

Situaciones como estas pueden ser salvadas si el profesor pone cuidado en instrumentar actividades donde los estudiantes construyan y comprendan cabalmente los puentes que conectan la aritmética con el álgebra, por ejemplo, la representación desarrollada del número 123 es 1×10² + 2×10¹ + 3×10⁰;  y un polinomio es la representación más general del número donde x representa la base numérica, así, escribir 123 como  x² + 2x + 3, esto es, un polinomio de grado 2 en base x=10 puede darle claridad al alumno sobre las diferentes representaciones de un mismo número.

 D) La naturaleza y significado de los símbolos y las letras en aritmética y álgebra

 En este apartado queremos ilustrar algunas situaciones donde los estudiantes le dan significado en un contexto y en otro a los mismos símbolos y cómo esto influye, muchas veces, en una errónea conceptualización.

Los cambios conceptuales muchas veces provocan errores en quienes son noveles en su uso y hacen transferencias ingenuas de significados de un contexto a otro. Con frecuencia, los alumnos fallan al asumir cambios conceptuales convencionales y se tienen que contentar con conocer que existen situaciones nuevas donde su conocimiento es inadecuado, inapropiado o incompleto, resistiéndose a efectuar las correcciones de pensamiento. El mayor cambio conceptual en el aprendizaje del álgebra se centra alrededor de su diferencia con la aritmética: los símbolos significan a veces cosas distintas, parecidas o iguales a las que se conocían y hay que distinguir entre estos casos, asimismo, hay una diferente interpretación de las letras (literales) y los métodos y procesos analíticos que son el foco de atención en álgebra, puesto que le dan un sentido concreto a la abstracción sobre las generalizaciones acerca de la cantidad y el número, en contraposición a la mera búsqueda de un resultado numérico, como acontece con los problemas de la aritmética.

Para poder operar con abstracciones necesitamos nombrarlas o denotarlas, los símbolos son un recurso idóneo para hacerlo. Una de las tareas de los estudiantes que se inician en el álgebra, es el reconocimiento de la naturaleza y significado de los símbolos para poder comprender cómo operar con ellos y cómo interpretar los resultados. Este reconocimiento con comprensión, es el que les permite hacer la transferencia de sus conocimientos aritméticos a los algebraicos, reconociendo y aceptando las diferencias entre ambos. El discernimiento del significado de los valores simbólicos les puede llevar a dar 7x como respuesta de 3x + 4 —como ya expusimos anteriormente— que tienen que ver con su interpretación del símbolo de la operación +. En aritmética el símbolo + es interpretado como una acción a realizar, es decir, “más” significa realizar la operación de añadir. Pero en álgebra hay un cambio sustancial, ahora “virtualmente el mismo más” representa e indica a la vez el resultado y la acción simultáneamente, cosa que no es fácilmente percibida por los alumnos, aun cuando estas dos nociones son necesarias para el conocimiento del álgebra:  3x + 4 representa el triple de una cantidad aumentada en 4, no es “una mera suma” nada más. Los estudiantes trasladan los objetivos de la aritmética —buscar un resultado numérico— al álgebra, este patrón de pensamiento es más frecuente de lo que muchos profesores se imaginan, al menos en nuestras aulas del bachillerato en México, es del orden del 94%.[2]

Para poder operar con “valores simbólicos”, el estudiante requiere ampliar su concepto de notación usado en la aritmética. Sucede con frecuencia que los alumnos reducen la comprobación de la validez de una transformación algebraica con la verificación aritmética en un ejemplo —caso particular de la expresión algebraica—. Para ellos, el lenguaje algebraico presenta ambigüedades y dualidad de significados, cosa que les provoca confusión en el intento de relacionar la representación numérica (primitiva) con la simbólica más evolucionada.

En aritmética los símbolos poseen su valor dependiendo de la posición que ocupen en la expresión «a cada lugar, un valor». Un error común de los estudiantes de álgebra es inducir que si x = 7  entonces  4x = 47. También, con la notación de números mixtos como      —que significa la suma de 7 enteros y un medio— los estudiantes trasladan esto a expresiones como xy dados x = ‑ 4   e  y = ‑ 3 interpretándolas, como xy = ‑ 7, donde han sumado en lugar de multiplicar, en estos casos sería aconsejable seguir escribiendo el signo de la multiplicación por un tiempo razonable cuando se trabaja con productos algebraicos para evitar estas equivocaciones.

Otro factor de confusión es la comprensión, en un sentido más amplio, del signo igual; aspecto relacionado con el concepto de igualdad que en aritmética normalmente conecta un problema con su resultado numérico, —    5 + 6 = 11   —, y pocas veces la equivalencia de procesos como en 2  5 = 5 + 5; en cambio en álgebra, con mayor frecuencia el mismo signo «=» conecta dos procesos que valen lo mismo o que son equivalentes.

En álgebra, el uso del « = » representa cambios conceptuales de fondo, ya que puede ser usado en varios sentidos, por ejemplo: en la expresión  x = 3 puede ser leído, según el contexto matemático donde se use, como la asignación del valor 3 a la variable x, o también como una recta paralela al eje Y que corta al eje X en el punto 3; es decir, representa una región en el plano donde los puntos son de la forma (3, y); también puede ser el último paso de un despeje en una ecuación y representar la solución de la misma. A diferencia de otros símbolos, como ya vimos, el uso del signo « = » representa en álgebra, un conflicto para el estudiante, pues debe extender o ampliar en su mente sus significados y, al mismo tiempo, debe estar muy alerta del contexto matemático en el que lo maneja.

Los usos inadecuados de este símbolo conducen a reforzar las concepciones erróneas de los estudiantes ancladas en la aritmética y que tal cual, trasladan al álgebra, así, encontramos cadenas de iguales «=» que no son iguales como en el siguiente ejemplo resuelto por un alumno:       16 – 3 × 4 + 1 = 16 – 12 = 4 + 1 = 5

 donde la expresión numérica después del primer « = » no tiene el mismo valor que su antecesora y sucesora.

En aritmética, el sentido del signo igual es casi siempre unidireccional, es decir, antecede a un resultado numérico. Los alumnos trasladan a veces este significado del signo « = » al álgebra y lo confunden con el « = » de la ecuación, o con el de proporción, el de equivalencia, el de identidad y el de asignación de valor a una variable, incógnita o literal.

Ecuaciones como  3x + 3 = 2x + 7,  a diferencia de las expresiones aritméticas como 5 + 3×4 = 15 + 2, no son afirmaciones verdaderas y universales (identidades o equivalencias), es decir, el signo «=» obliga a la incógnita a tomar un valor para que la expresión sea verdadera. A los estudiantes les cuesta trabajo interiorizar esta variedad de significados del signo igual, que puede estar expresando una equivalencia y no una invitación a escribir el resultado. Algunos de los problemas que el uso del símbolo del igual plantea a los estudiantes, se pueden presentar en casos como los que se mencionan a continuación.

¿Cantidades variables o números únicos? Las letras en aritmética representan cosas distintas que en álgebra, esas diferencias de significado son fuente de confusión en el estudiante porque, por ejemplo, en aritmética la «m» o la «g» representan metros y gramos (unidades de medida) y en álgebra pueden estar representando la cantidad en metros, en gramos o de cualquier otra cosa —comúnmente una función— y, para colmo, la idea de que esta representación se refiera a una variable, va en contra de su concepción de considerar a las letras como valores únicos y específicos, como en el caso de la expresión d + 5 = 7  y no variables como en las expresiones   w + z = z + w  o  B = z•w.

Propuestas de solución

Conocer, de alguna manera, cómo construyen nuestros estudiantes su conocimiento algebraico y la forma en que articulan su pensamiento alrededor de dicho conocimiento, requirió de analizar algunas de las posibles fuentes donde se originan los errores conceptuales y de procedimiento en las mentes de nuestros pupilos. Los profesores debemos saber, lo más profundamente posible, sobre este proceso de construcción del conocimiento de los alumnos si queremos que obtengan mejores aprendizajes.

Como resultado de nuestros trabajos de investigación (Flores et al, 2016), creemos conveniente sugerir a los docentes que realicen diagnósticos de los errores que cometen sus estudiantes. La revisión analítica de los errores tiene un doble propósito: por un lado, sirve para ayudar a los profesores a una mejor conducción de la enseñanza aprendizaje del álgebra, insistiendo en aquellos aspectos en los cuales los aprendices tienden a construir concepciones erróneas y, por otro, aporta información sustantiva acerca de los elementos esenciales de las habilidades cognitivas a desarrollar que se deben tomar en cuenta para la planeación y el diseño didáctico que lleven a los alumnos a mejorar una construcción mental de las mismas y, por ende, a que superen los errores que obstaculizan sus aprendizajes en matemáticas.

Los profesores debemos estar atentos a los errores específicos que cometan los estudiantes y darles primeramente, la oportunidad de que sean ellos quienes los revisen e intenten su corrección para superarlos. Los alumnos que son capaces de verificar por sí mismos, mediante pruebas, la corrección de sus respuestas así como la aplicación a la generalidad de los casos, no tienen realmente problemas en álgebra pero, si por el contrario, un estudiante comete con frecuencia el mismo tipo de errores, ese hecho está señalando que existe un problema conceptual que requiere atención especial, pues se trata de una dificultad en aritmética y en álgebra que el estudiante toma por conocimiento válido sin someterlo a prueba.

En el proceso de la superación de los propios errores, la participación activa del alumno es fundamental, ya que nadie aprende por otro, para lograr esto, el profesor le ayuda provocando conflicto entre lo que el estudiante piensa y lo que se plantea en clase, haciéndole notar la inconsistencia de sus propios errores y forzándolo a actuar en la resolución del conflicto cognitivo para que sustituya los conceptos erróneos por los adecuados.

En la enseñanza de las matemáticas el profesor con orientación constructivista rara vez indica a los alumnos cuál es la respuesta correcta, ellos deben hallarla por sí mismos, para ello, simplemente les pide comprobaciones y pruebas que intenten hacerlos caer en contradicciones que resultan de sus falsos conceptos. La labor del profesor en la instrucción es dirigirlos a la resolución de las contradicciones a través de estrategias de aprendizaje que demanden a los alumnos fundamentar y comprobar sus respuestas y resultados, no se trata de que nada más den o reciten la fórmula o regla de procedimiento, —sin ser capaces de captar e interpretar sus significados— ya que precisamente el aprendizaje memorístico de fórmulas, como ya se sabe, puede conducirlos a errores. La esencia de la instrucción en las matemáticas consiste en comprometer a los estudiantes a enfrentarse con las contradicciones —propias y ajenas— para que las falsas concepciones sean erradicadas de su mente y cambiadas por las adecuadas.

Con respecto a la comprensión de la aritmética por parte de los aprendices, ya hemos mostrado anteriormente, en algunos ejemplos, el tipo de transferencia de conocimientos e ideas que hacen desde su aritmética hacia el álgebra, para superar esto, los profesores debemos instrumentar estrategias de enseñanza-aprendizaje, donde los pupilos puedan discernir sobre las similitudes entre ambas ramas de las matemáticas y reconocer claramente las diferencias entre ellas.

Recalcar que en general la variedad de dificultades que tienen los alumnos con el aprendizaje de la aritmética y el álgebra, ya descritas anteriormente, están fuertemente interrelacionadas con situaciones afectivas y actitudes con bases no racionales hacia las matemáticas.

Al trabajar con las «matemáticas de los estudiantes» y operar con sus ideas previas —convertidas en obstáculos de aprendizaje—, debemos intervenir en un nivel de prevención y combinar estrategias de enseñanza generales y, a largo plazo, estrategias particulares e inmediatas. El profesor debe entender los errores específicos del alumno, como una información parcial de las dificultades en el aprendizaje de la aritmética y el álgebra —e ir más allá— es decir, debe buscar la concreción de la filosofía educativa, razón de ser del CCH, que consiste en promover la formación de alumnos independientes en su aprendizaje (aprender a aprender), capaces de valorarse a sí mismos y a los demás (aprender a ser), convertirse en individuos con espíritu crítico capaces de resolver problemas (aprender a hacer) que requiere un refuerzo específico y, rechazar la falsa idea de que dichos errores provienen de descuidos por una virtual falta de atención o aparente incapacidad intelectual por parte de nuestros estudiantes.

Asimismo, la verificación de los aprendizajes debe hacerse de manera conjunta, alumno-profesor. Debe ser fina, revisar procesos de análisis, representación y resolución de problemas y fenómenos. Si no hay recursos de apoyo psicopedagógico, por lo menos podemos irnos acercando, con nuestros recursos a la mano, a dar una atención personalizada, rápida y oportuna a nuestros alumnos.

Sería deseable que cada profesor se aboque a saber un poco más del origen de las dificultades en el aprendizaje del álgebra en sus alumnos y hallar alternativas que puedan superarlas con objeto de mejorar el aprovechamiento académico en matemáticas.

En el siguiente punto exponemos algunas sugerencias de estrategias didácticas que, pensamos, atienden algunas de las problemáticas señaladas en el rubro III.

 [2] Medido a través de una década con exámenes de problemas en una población acumulada de 3500 estudiantes  (1993-2002). Algunos estudiantes lo dejan como está, lo cual es correcto, pero tienen dudas y no saben explicar ni leer la expresión algebraica, por eso se eleva el porcentaje de estudiantes con este fallo.

[3] En la programación de rutinas (procesos computacionales) que se ejecutan iteradamente y donde el valor de la variable se incrementa en uno cada vez que se lleva a cabo dicho procedimiento.